Bootstrap i R
Bootstrap er en metode til indledning om en population ved hjælp af prøvedata.Bradley Efron introducerede det først i dettepapir i 1979.Bootstrap er afhængig af prøveudtagning med udskiftning fra prøvedata. Denne teknik kan bruges til at estimere standardfejlen for enhver statistik og opnå et konfidensinterval (CI) for det. Bootstrap er især nyttignår CI ikke har en lukket form, eller den har en meget kompliceret.
Antag, at vi har en prøve af N elementer:h = {h1, h2,…, HN} og slid interesseret i CI for nogle statistik T = t(H). Bootstrapramme er ligetil. Vi gentager bare r gange følgende ordning: for i-TH gentagelse, prøve med udskiftning n elementer fratilgængelig prøve (nogle af dem vil blive plukket mere end en gang). Dette er en ny prøve i-TH bootstrap-prøve, og beregnet til den ønskede statistik Ti = t(I).
som følge heraf får vi R-værdier af vores statistik: T1, T2,…, TR. Vi kalder dembootstrap-realiseringer af T eller en bootstrap-distribution af T. baseret på det kan vi beregne CI for T. der er flere måder at gøre dette på. At tage percentiler synes at være den nemmeste.
Bootstrap i aktion
lad os bruge (igen) velkendt iris datasæt. Tag et kig på en førstefå rækker:
Antag, at vi vil finde CIs for median Sepal.Length, medianSepal.Width og Spearmans rang korrelationskoefficient mellem disseto. Vi bruger R‘s boot pakke og en funktion kaldet… boot. Touse sin magt, vi er nødt til at skabe en funktion, der beregner ourstatistic(s) ud af resampled data. Det skal have mindst toargumenter: a dataset og en vektor indeholdende indices af elementer fra et datasæt, der blev valgt for at oprette en bootstrap-prøve.
hvis vi ønsker at beregne CIs for mere end en statistik på en gang, skal ourfunction returnere dem som en enkelt vektor.
for vores eksempel kan det se sådan ud:
library(boot)foo <- function(data, indices){ dt<-data c( cor(dt, dt, method='s'), median(dt), median(dt) )}foo vælger ønskede elementer (hvilke tal er gemt i indices)fra data og beregner korrelationskoefficient for de første to kolonner (method='s' bruges til at vælge Spearmans rangkoefficient,method='p' vil resultere med Pearsons koefficient) og deres medianer.
vi kan også tilføje nogle ekstra argumenter, f.eks. lad brugeren vælge type odcorrelationskoefficient:
foo <- function(data, indices, cor.type){ dt<-data c( cor(dt, dt, method=cor.type), median(dt), median(dt) )}for at gøre denne tutorial mere generel bruger jeg sidstnævnte version affoo.
nu kan vi bruge funktionen boot. Vi er nødt til at forsyne det med et navn oddataset, funktion, som vi lige har oprettet, antal gentagelser (R)og eventuelle yderligere argumenter for vores funktion (som cor.type). Nedenfor, ibrug set.seed til reproducerbarhed af dette eksempel.
set.seed(12345)myBootstrap <- boot(iris, foo, R=1000, cor.type='s')boot funktion returnerer et objekt af klassen kaldet… (ja, du har ret!)boot. Det har to interessante elementer. $t indeholder R-værdier af ourstatistic (s) genereret af bootstrap-proceduren (bootstrap realisations ofT):
$t0 indeholder værdier af vores statistik(r) i original, fuld, datasæt:
myBootstrap$t0## -0.1667777 5.8000000 3.0000000udskrivning boot objekt til konsollen giver nogle yderligere oplysninger:
original er det samme som $t0. bias er en forskel mellem gennemsnittet afbootstrap realiseringer (dem fra $t), kaldet et bootstrap estimateof T og værdi i originalt datasæt (den fra $t0).
colMeans(myBootstrap$t)-myBootstrap$t0## 0.002546391 -0.013350000 0.007900000std. error er en standardfejl i bootstrap estimat, hvilket svarer tilstandardafvigelse af bootstrap realiseringer.
apply(myBootstrap$t,2,sd)## 0.07573983 0.10295571 0.02726414forskellige typer bootstrap CIs
før vi starter med CI, er det altid værd at tage et kig pådistribution af bootstrap realiseringer. Vi kan bruge plot funktion, med index fortæller på hvilken af statistikker beregnet i foo vi ønsker Atse. Her index=1 er en Spearmans korrelationskoefficient mellemsepal længde og bredde, index=2 er en median od sepal længde, ogindex=3er en median od sepal bredde.
plot(myBootstrap, index=1)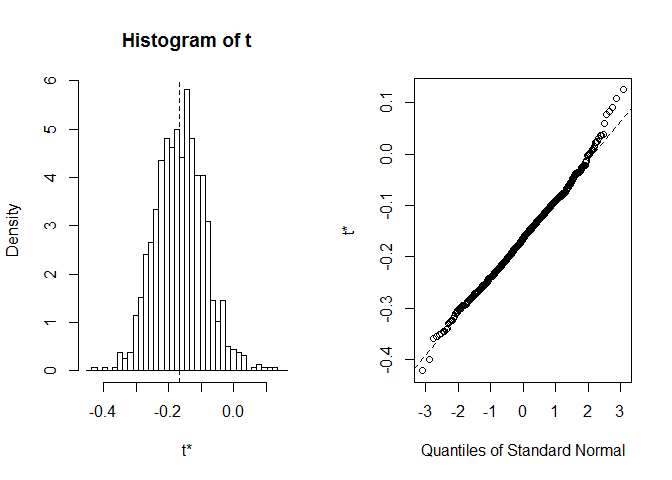
fordeling af Bootstrap korrelationskoefficienter virker retnormallignende. Lad os finde CI for det. Vi kan bruge boot.ci. Det er standard til95 procent CIs, men det kan ændres med parameteren conf.
boot.ci giver 5 typer bootstrap CIs. En af dem, studeretinterval, er unik. Det har brug for et skøn over bootstrap varians. Vi giver det ikke, så R udskriver en advarsel:bootstrap variances needed for studentized intervals. Variansestimater kan opnås med anden niveau bootstrap eller (lettere) medjackknife teknik. Dette er på en eller anden måde uden for rammerne af denne tutorial,så lad os fokusere på de resterende fire typer bootstrap CIs.
hvis vi ikke ønsker at se dem alle, kan vi vælge relevante i type argument. Mulige værdier er norm, basic, stud, perc, bca ora vektor af disse.
funktionen boot.ci opretter objekt af klasse… (ja, du har gættet!)bootci. Dens elementer kaldes ligesom typer af CI anvendt i type argument. $norm er en 3-element vektor, der indeholder konfidensniveauog ci grænser.
boot.ci(myBootstrap, index=1, type='norm')$norm## conf ## 0.95 -0.3177714 -0.02087672$basic, $stud, $perc og $bca er 5-element vektorer indeholdendeogså percentiler bruges til at beregne CI (vi kommer tilbage til dette senere):
boot.ci(myBootstrap, index=1, type='basic')$basic## conf ## 0.95 975.98 25.03 -0.3211981 -0.03285178lidt notation (Undskyld!)
for at få en fornemmelse af, hvad forskellige typer CI er, skal vi introducerenogle notationer. Så lad:
- t⋆ være bootstrap skøn (gennemsnit af bootstraprealizations),
- t0 være en værdi af vores statistik i det oprindelige datasæt,
- se⋆ være en standard fejl af bootstrap skøn,
- b være en bias af bootstrap-estimateb = t⋆ − t0
- α være en grad af tillid, typisk α = 0.95,
- za være et $1-\frac \alpha 2$-fraktilen af standardnormal distribution,
- θα være en α-fraktilen for fordelingen af bootstraprealizations.
percentil CI
med ovenstående notation er percentil CI:
så dette tager bare relevante percentiler. Ikke andet.
Normal CI
en typisk Vald CI ville være:
men i bootstrap tilfælde bør vi rette det for bias. Så det bliver:
$$ t_0 – B \pm å_\alpha \cdot se^\star \\2t_0 – T^\star \pm å_\alpha \cdot se^\star$$
grundlæggende CI
percentil CI anbefales generelt ikke, fordi det fungerer dårligtnår det kommer til underlige halefordelinger. Grundlæggende CI (også kaldetpivotal eller empirisk CI) er meget mere robust til dette. Det rationeltbag det er at beregne forskelle mellem hver bootstrap-replikationog t0 og bruge percentiler af deres distribution. Alle statistikker
den endelige formel for grundlæggende CI er:
BCa CI
BCa kommer fra bias-korrigeret, accelereret. Formlenfor det er ikke meget kompliceret, men noget uintuitivt, så jeg springer over det.Se artikel af Thomas J. DiCiccio og BradleyEfron, hvis du er interesseret i detaljer.
Acceleration nævnt i metodens navn kræver brug af specifikkepercentiler af bootstrap-realiseringer. Nogle gange kan det ske, atdisse ville være nogle ekstreme percentiler, muligvis outliers.BCa kan være ustabil i sådanne tilfælde.
lad os se på BCa CI for kronblad bredde median. Inoriginal datasæt, Denne median er lig med præcist 3.
vi får BCa CI (2, 9, 2, 9). Det er underligt, men heldigvis Radvarede os om, at extreme order statistics used as endpoints. Lad os sehvad der nøjagtigt skete her:
plot(myBootstrap, index=3)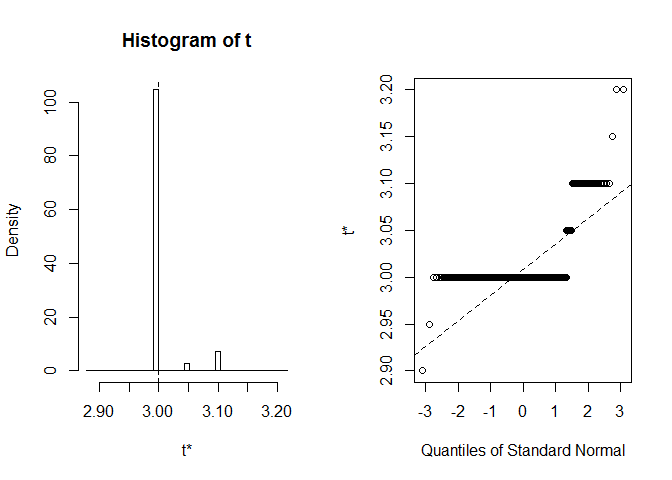
Distribution af bootstrap-realiseringer er usædvanlig. Langt de fleste af dem (over 90%) er 3s.
table(myBootstrap$t)#### 2.9 2.95 3 3.05 3.1 3.15 3.2## 1 1 908 24 63 1 2replikation af resultater
nogle gange er vi nødt til at genskabe bootstrap-replikationer. Hvis vi kan bruge Rtil det, er dette ikke et problem. set.seed funktion løser problemet.Genskabelse af bootstrap replikationer i andre programmer ville være meget merevanskelig. Hvad mere er, for stor R kan genberegning i R ogsåikke være en mulighed (på grund af manglende tid, for eksempel).
vi kan håndtere dette problem ved at gemme indekser af elementer af originaldataset, der dannede hver bootstrap-prøve. Dette er hvad boot.arrayfunktion (med indices=T argument) gør.
tableOfIndices<-boot.array(myBootstrap, indices=T)hver række er en bootstrap-prøve. Fx., vores første prøve indeholderfølgende elementer:
indstilling indices=F (en standard), vi får svar på spørgsmålet “Hvordanmange gange dukkede hvert element i det originale datasæt op i hver bootstrapsample?”. For eksempel i den første prøve: det 1.element i datasættet dukkede open gang viste 2. element slet ikke, 3. element dukkede op en gang, 4. to gange og så videre.
en tabel som denne giver os mulighed for at genskabe bootstrap realisering udenfor R.Eller i R sig selv, når vi ikke ønsker at bruge set.seed og gøre al thecomputation igen.
onceAgain<-apply(tableOfIndices, 1, foo, data=iris, cor.type='s')lad os kontrollere, om resultaterne er de samme:
Ja, de er!
hvis du gerne vil lære mere om maskinindlæring i R, skal du tage DataCamp ‘ s værktøjskasse til maskinindlæring.