brug af logaritmer i den virkelige verden
logaritmer er overalt. Brug nogensinde følgende sætninger?
- 6 tal
- Dobbeltcifre
- størrelsesorden
- rente
du beskriver tal med hensyn til deres beføjelser på 10, en logaritme. Og en rente er logaritmen for væksten i en investering.
overrasket over, at logaritmer er så almindelige? Også mig. De fleste forsøg på matematik i den virkelige verden (TM) peger på logaritmer i nogle arcane formel, eller lade som om vi er geologer fascineret af Richter skalaen. “Forskere bekymrer sig om logfiler, og det skal du også. Og kan man forestille sig en verden uden sol?”
nej, nej, nej, nej nej, nej nej! (Mama mia!)
matematik udtrykker begreber med notation som “ln” eller “log”. At finde “matematik i den virkelige verden” betyder at møde ideer i livet og se, hvordan de kunne skrives med notation. Se ikke efter de bogstavelige symboler! Hvornår var sidste gang du skrev et divisionstegn? Hvornår har du sidst hugget noget mad op?
Ok, ok, vi får det: hvad handler logaritmer om?
logaritmer finder årsagen til en effekt, dvs.input til noget output
en fælles “effekt” ser noget vokse, som at gå fra \$100 til \$150 om 5 år. Hvordan skete det? Vi er ikke sikre, men logaritmen finder en mulig årsag: et kontinuerligt afkast på ln(150/100) / 5 = 8,1% ville tegne sig for denne ændring. Det er måske ikke den egentlige årsag (skete al væksten i det sidste år?), men det er et glat gennemsnit, Vi kan sammenligne med andre ændringer.
forresten er begrebet “årsag og virkning” nuanceret. Hvorfor er 1000 større end 100?
- 100 er 10 der voksede af sig selv i 2 tidsperioder ($10 * 10$)
- 1000 er 10 som voksede af sig selv i 3 tidsperioder ($10 * 10 * 10$)
vi kan tænke på tal som udgange (1000 er “1000 udgange”) og indgange (“hvor mange gange skal 10 vokse for at gøre disse udgange?”). Så,
1000 outputs > 100 outputsfordi
3 inputs > 2 inputseller med andre ord:
log(1000) > log(100)Hvorfor er dette nyttigt?
logaritmer sætter tal på en menneskevenlig skala.
store tal bryder vores hjerner. Millioner og billioner er “virkelig store”, selvom en million sekunder er 12 dage og en billion sekunder er 30.000 år. Det er forskellen mellem et amerikansk ferieår og hele den menneskelige civilisation.
tricket til at overvinde “stort antal blindhed” er at skrive tal i form af “input” (dvs.deres magtbase 10). Denne mindre skala (0 til 100) er meget lettere at forstå:
- magt af 0 = $10^0$ = 1 (enkelt element)
- magt af 1 = $10^1$ = 10
- effekt på 3 = $10^3$ = tusind
- effekt på 6 = $10^6$ = millioner
- effekt på 9 = $10^9$ = milliarder
- effekt på 12 = $10^12$ = billioner
- effekt på 23 = $10^23$ = antal molekyler i et dusin gram kulstof
- effekt på 80 = $10^80$ = antal molekyler i universet
en 0 til 80 skala tog os fra et enkelt element til antallet af ting i universet. Ikke for lurvet.
logaritmer tæller multiplikation som trin
logaritmer beskriver ændringer med hensyn til multiplikation: i eksemplerne ovenfor er hvert trin 10 gange større. Med den naturlige log er hvert trin “e” (2.71828…) gange mere .
når man beskæftiger sig med en række multiplikationer, hjælper logaritmer med at “tælle” dem, ligesom tilføjelse tæller for os, når effekter tilføjes.
Vis mig matematikken
tid til kødet: lad os se, hvor logaritmer dukker op!
sekscifret løn eller 2-cifret udgift
vi beskriver tal i form af deres cifre, dvs. hvor mange kræfter på 10 de har (er de i tiere, hundreder, tusinder, ti tusinder osv.). Tilføjelse af et ciffer betyder “multiplicere med 10”, dvs.
![]()
logaritmer tæller antallet af multiplikationer tilføjet, så startende med 1 (et enkelt ciffer) tilføjer vi 5 flere cifre ($10^5$) og 100.000 får et 6-cifret resultat. At tale om” 6 “i stedet for” hundrede tusind ” er essensen af logaritmer. Det giver en grov følelse af skala uden at hoppe ind i detaljer.
Bonus spørgsmål: Hvordan vil du beskrive 500.000? At sige “6 figur” er vildledende, fordi 6-tal ofte indebærer noget tættere på 100.000. Ville” 6.5 figur ” arbejde?
ikke rigtig. I vores hoveder betyder 6,5 “halvvejs” mellem 6 og 7 figurer, men det er en adders tankegang. Med logaritmer a”.5 ” betyder halvvejs i form af multiplikation, dvs.kvadratroden ($9^.5$ betyder kvadratroden af 9 — 3 er halvvejs i form af multiplikation, fordi det er 1 til 3 og 3 til 9).
ved at tage log(500.000) får vi 5,7, tilføjer 1 For det ekstra ciffer, og vi kan sige “500.000 er en 6.7 figur nummer”. Prøv det her:
størrelsesorden
vi nørder elsker denne sætning. Det betyder omtrent “10 gange forskel”, men lyder bare køligere end”1 ciffer større”.
i computere, hvor alt tælles med bits (1 eller 0), har hver bit en fordoblingseffekt (ikke 10 gange). Så at gå fra 8 til 16 bit er “8 størrelsesordener” eller $2^8 = 256$ gange større. (“Større” henviser i dette tilfælde til den mængde hukommelse, der kan adresseres.) At gå fra 16 til 32 bit betyder en ekstra 16 størrelsesordener eller $2^16$ ~ 65.536 gange mere hukommelse, der kan adresseres.
rentesatser
Hvordan finder vi ud af vækstrater? Et land har ikke til hensigt at vokse med 8,56% om året. Du ser på BNP et år og BNP det næste, og tag logaritmen for at finde den implicitte vækstrate.
Mine to foretrukne fortolkninger af den naturlige logaritme(ln)), dvs. den naturlige log af 1.5:
- hvis du antager 100% vækst, hvor længe skal du vokse for at komme til 1,5? (.405, mindre end halvdelen af tidsperioden)
- forudsat 1 tidsenhed, hvor hurtigt skal du vokse for at komme til 1,5? (40.5% om året, kontinuerligt sammensat)
logaritmer er, hvordan vi finder ud af, hvor hurtigt vi vokser.
måleskala: Google PageRank
Google giver hver side på nettet en score (PageRank), som er et groft mål for autoritet / betydning. Dette er en logaritmisk skala, som i mit hoved betyder “PageRank tæller antallet af cifre i din score”.
så et sted med pagerank 2 (“2 cifre”) er 10 gange mere populært end et PageRank 1-sted. Min side er PageRank 5 og CNN har PageRank 9, så der er en forskel på 4 størrelsesordener ($10^4$ = 10,000).
groft sagt får jeg omkring 7000 besøg / dag. Ved hjælp af min konvolut matematik kan jeg gætte CNN får omkring 7000 * 10.000 = 70 millioner besøg / dag. (Hvordan gjorde jeg det ? I mit hoved tror jeg $7k * 10k = 70 * k * k = 70 * M$). De kan have et par gange mere end det (100m, 200m), men sandsynligvis ikke op til 700m.
Google formidler en masse information med en meget grov skala (1-10).
måleskala: Richter, Decibel osv.
Suk. Vi er ved de typiske “logaritmer i den virkelige verden” eksempel: Richter skala og Decibel. Ideen er at sætte begivenheder, der kan variere drastisk (jordskælv) på en enkelt skala med et lille interval (typisk 1 til 10). Ligesom PageRank er hver 1-punkts stigning en 10 gange forbedring af strømmen. Det største jordskælv, der blev registreret af mennesker, var 9,5; virkningen på Yucat-halvøen, som sandsynligvis gjorde dinosaurerne uddøde, var 13.
decibel er ens, selvom det kan være negativt. Lyde kan gå fra intenst stille (pindrop) til ekstremt højt (fly), og vores hjerner kan behandle det hele. I virkeligheden er lyden af et flys motor millioner (milliarder, billioner) gange kraftigere end en pindrop, og det er ubelejligt at have en skala, der går fra 1 til en gasillion. Logs holder alt på en rimelig skala.
logaritmiske grafer
du vil ofte se emner afbildet på en “logskala”. I mit hoved betyder det, at den ene side tæller “antal cifre” eller “antal multiplikationer”, ikke selve værdien. Igen hjælper dette med at vise vildt varierende begivenheder på en enkelt skala (går fra 1 til 10, ikke 1 til milliarder).
Moores lov er et godt eksempel: vi fordobler antallet af transistorer hver 18. måned.
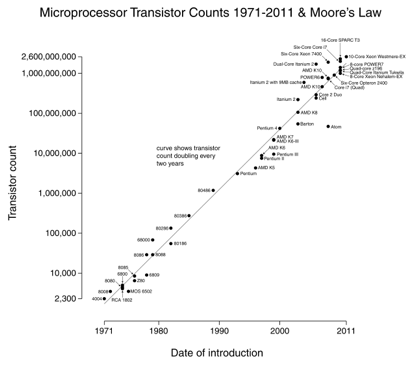
det pæne ved logskala grafer er eksponentielle ændringer (processorhastighed) vises som en lige linje. At vokse 10 gange om året betyder, at du støt marcherer op på “cifrene” skalaen.
fremad og opad
hvis et koncept er velkendt, men ikke elsket, betyder det, at vi er nødt til at opbygge vores intuition. Find de analogier, der virker, og ikke nøjes med slop en lærebog vil trav ud. I mit hoved:
- logaritmer finder grundårsagen til en effekt (se vækst, find rente)
- de hjælper med at tælle multiplikationer eller cifre med bonus på delvise tællinger (500k er et 6,7 cifret tal)
glad matematik.
andre indlæg i denne serie
- en intuitiv Guide til eksponentielle funktioner & e
- afmystificering af den naturlige logaritme (ln)
- en visuel Guide til enkle, sammensatte og kontinuerlige renter
- fælles definitioner af e (farvet)
- forståelse eksponenter (hvorfor 0^0 = 1?)
- brug af logaritmer i den virkelige verden
- Sådan tænker du med eksponenter og logaritmer
- forståelse diskret vs. kontinuerlig vækst
- hvad betyder en eksponent virkelig?
- spørgsmål: Hvorfor er e speciel? (2.718…, ikke 2, 3.7 eller et andet nummer?)