Bootstrap v R
Bootstrap je metoda odvozování o populaci pomocí vzorových dat.Bradley Efron to poprvé představil v tomtopapír v roce 1979.Bootstrap spoléhá na vzorkování s náhradou z ukázkových dat. Tato technika může být použita k odhadu standardní chyby jakékoli statistiky a k dosažení intervalu spolehlivosti (CI). Bootstrap je obzvláště užitečnýkdyž CI nemá uzavřenou formu nebo má velmi komplikovanou.
Předpokládejme, že máme vzorek n prvků: X = {x1, x2,…, xn} a máme zájem o CI pro nějakou statistiku T = t(X). Bootstrapframework je jednoduchý. My jen opakovat R krát followingscheme: Pro i-té opakování, vzorek s náhradou n prvků z dosažitelné vzorku (některé z nich bude vybrána více než jednou). Zavolejte tento nový vzorek i-tého vzorku bootstrapu, Xi a vypočítejte požadovanou statistiku Ti = T (Xi).
v důsledku toho získáme R hodnoty naší statistiky: T1, T2,…, TR. Říkáme jim Bootstrap realizace T nebo bootstrap distribuce T. Na základě toho můžeme vypočítat CI PRO T. existuje několik způsobů, jak to udělat. Užívání percentilů se zdá být nejjednodušší.
Bootstrap v akci
použijme (ještě jednou) známou iris dataset. Podívejte se na firstfew řádky:
Předpokládejme, že chceme najít CIs pro střední Sepal.Length, mediánSepal.Width a spearmanova pořadová korelační koeficient mezi dvě. Budeme používat R ‚ s boot balíček a funkce s názvem… boot. Využívat jeho sílu, musíme vytvořit funkci, která vypočítá ourstatistic(y) z převzorkování dat. Měl by mít alespoň dvě položky: dataset a vektor obsahující indices prvků z datové sady, které byly vybrány pro vytvoření vzorku bootstrapu.
pokud chceme vypočítat CIs pro více než jednu statistiku najednou, naše funkce je musí vrátit jako jeden vektor.
Pro náš příklad, to může vypadat takhle:
library(boot)foo <- function(data, indices){ dt<-data c( cor(dt, dt, method='s'), median(dt), median(dt) )}foo vybere požadované prvky (která čísla jsou uloženy v indices) data a vypočítá korelační koeficient první dva sloupce(method='s' se používá k vybrat Spearman ‚ s rank koeficient,method='p' bude mít s Pearsonův koeficient) a jejich mediány.
můžeme také přidat některé další argumenty, např. nechte uživatele zvolit typ odcorelační koeficient:
foo <- function(data, indices, cor.type){ dt<-data c( cor(dt, dt, method=cor.type), median(dt), median(dt) )}aby byl tento tutoriál obecnější, použiji druhou verzifoo.
Nyní můžeme použít funkci boot. Musíme mu dodat název oddataset, funkci, kterou jsme právě vytvořili, počet opakování (R) a další argumenty naší funkce (jako cor.type). Níže, Iuse set.seed pro Reprodukovatelnost tohoto příkladu.
set.seed(12345)myBootstrap <- boot(iris, foo, R=1000, cor.type='s')boot funkce vrací objekt volané třídy… (ano, máte pravdu!)boot. Má dva zajímavé prvky. $t obsahuje R hodnoty ourstatistic(s) generované postup bootstrap (bootstrap realizace ofT):
$t0 obsahuje hodnoty naší statistika(y) v původní, plné, dataset:
myBootstrap$t0## -0.1667777 5.8000000 3.0000000Tisk boot objekt do konzoly dává nějaké další informace:
original je to stejné jako $t0. bias je rozdíl mezi tím ofbootstrap realizace (ty z $t), tzv. bootstrap estimateof T a hodnotu v původní datové sady (jedna z $t0).
colMeans(myBootstrap$t)-myBootstrap$t0## 0.002546391 -0.013350000 0.007900000std. error je standardní chyba odhadu bootstrap, která se rovnástandardní odchylka realizací bootstrap.
apply(myBootstrap$t,2,sd)## 0.07573983 0.10295571 0.02726414Různé typy bootstrap CIs
předtím, Než začneme s CI, je to vždy stojí za to se podívat na konkrétní bootstrap realizace. Můžeme použít plot funkceindex říct, v které statistiky vypočtené v foo přejeme vypadat. Zde index=1 je Spearmanův korelační koeficient mezidélka a šířka, index=2 je střední délka od sepal aindex=3je střední šířka od sepal.
plot(myBootstrap, index=1)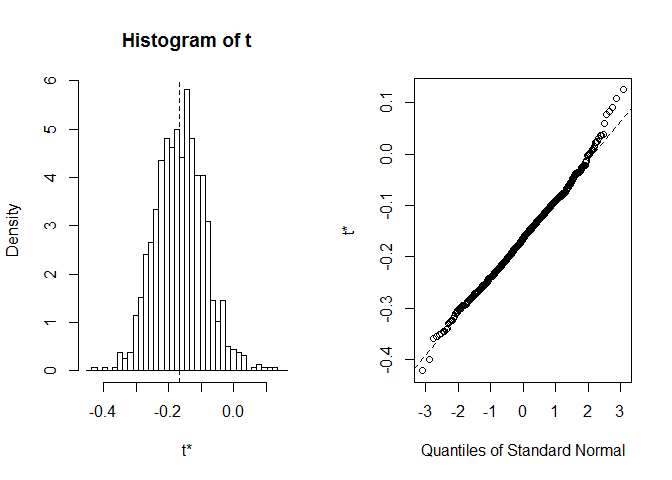
distribuce bootstrapových korelačních koeficientů se zdá být docelanormální. Najdeme pro to informátora. Můžeme použít boot.ci. Výchozí hodnota je 95% CIs, ale lze ji změnit parametrem conf.
boot.ci poskytuje 5 typů bootstrap CIs. Jeden z nich, studentizedinterval, je jedinečný. Potřebuje odhad rozptylu bootstrapu. Neposkytujeme jej, takže R vytiskne varování:bootstrap variances needed for studentized intervals. Varianceestimates lze získat pomocí bootstrap druhé úrovně nebo (jednodušší) s technikou jackknife. To je nějak nad rámec tohoto tutoriálu, takže se zaměřme na zbývající čtyři typy bootstrap CIs.
pokud je nechceme vidět všechny, můžeme vybrat relevantní v argumentu type. Možné hodnoty jsou norm, basic, stud, perc, bca nebo vektor těchto.
funkce boot.ci vytvoří objekt třídy… (ano, uhodli jste!)bootci. Jeho prvky se nazývají stejně jako typy CI používané v argumentu type. $norm je 3-elementový vektor, který obsahuje meze úrovně spolehlivosti CI.
boot.ci(myBootstrap, index=1, type='norm')$norm## conf ## 0.95 -0.3177714 -0.02087672$basic, $stud, $perc a $bca jsou 5-prvek vektorů containingalso percentily používá pro výpočet CI (vrátíme se k tomu později):
boot.ci(myBootstrap, index=1, type='basic')$basic## conf ## 0.95 975.98 25.03 -0.3211981 -0.03285178trochu notace (Omlouvám se!)
abychom získali pocit, jaké jsou různé typy CI, musíme zavéstnějaký zápis. Takže, nechte:
- t⋆ být bootstrap odhad (průměr bootstraprealizations),
- t0 být hodnota naší statistika v originální dataset,
- se⋆ být standardní chyba bootstrap odhad,
- b být zaujatost bootstrap estimateb = t⋆ − t0
- α být úroveň spolehlivosti, obvykle α = 0.95,
- za $1-\frac \alpha 2$-kvantil z standardnormal distribuce,
- θα být α-percentil distribuce bootstraprealizations.
percentil CI
s výše uvedenou notací je percentil CI:
takže to trvá jen relevantní percentily. Nic víc.
Normální CI
typický Wald CI by:
ale v bootstrap případě, že jsme měli to správné pro zaujatost. Tak to se stává:
$$ t_0 – b \pm z_\alpha \cdot se^\star \\2t_0 – t^\star \pm z_\alpha \cdot se^\star$$
Základní CI
Percentil CI je obecně nedoporučuje, protože to provádí poorlywhen to přijde divný-sledoval distribucemi. Základní CI (také nazývanýpivotální nebo empirický CI)je mnohem robustnější. The racionálníza ním je vypočítat rozdíly mezi jednotlivými replikacemi bootstrapu a t0 a použít percentily jejich distribuce. Fulldetails lze nalézt, např. v L. Wasserman je ofStatistics
Konečné vzorce pro základní CI je:
BCa CI
BCa pochází z bias-corrected, zrychlil. Vzorec pro to není příliš komplikovaný, ale poněkud neintuitivní, takže to přeskočím.Viz článek Thomase J. DiCiccio a BradleyEfron, pokud máte zájem o podrobnosti.
zrychlení uvedené v názvu metody vyžaduje použití specificpercentilů realizací bootstrapu. Někdy se může stát, že by to byly nějaké extrémní percentily, případně odlehlé hodnoty.BCa může být v takových případech nestabilní.
podívejme se na BCa CI PRO medián šířky okvětních lístků. V původním datovém souboru se tento medián rovná přesně 3.
dostaneme BCA CI (2.9, 2.9). To je divné, ale naštěstí Rnás varoval, že extreme order statistics used as endpoints. Podívejme se, co se tady přesně stalo:
plot(myBootstrap, index=3)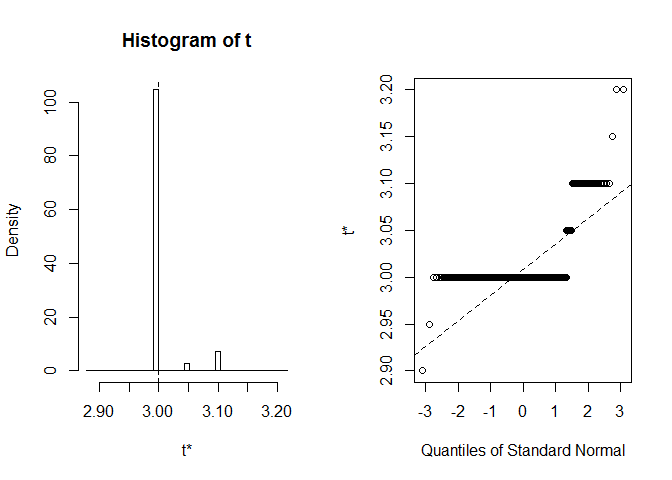
distribuce realizací bootstrapu je neobvyklá. Drtivá většina z nich (přes 90%) jsou 3s.
table(myBootstrap$t)#### 2.9 2.95 3 3.05 3.1 3.15 3.2## 1 1 908 24 63 1 2Replikace výsledků
Někdy musíme znovu vytvořit zaváděcí replikací. Pokud pro něj můžeme použít R, není to problém. set.seed funkce řeší problém.Obnovení replikací bootstrapu v jiném softwaru by bylo mnohem vícekomplikované. A co víc, pro velké R může být přepočet v R takénebýt volbou (například kvůli nedostatku času).
můžeme se vypořádat s tímto problémem, ukládání indexů prvků originaldataset, které tvořily každý vzorek bootstrap. To je to, co boot.arrayfunkce (s indices=T argumentem) dělá.
tableOfIndices<-boot.array(myBootstrap, indices=T)každý řádek je jeden vzorek bootstrapu. Ego. náš první vzorek obsahuje následující prvky:
Nastavení indices=F (výchozí), dostaneme odpověď na otázku „Kolik krát každý prvek původní dataset se objevil v každé bootstrapsample?“. Například v prvním vzorku: objevil se 1. prvek datové sady, 2. prvek se neobjevil vůbec, 3. prvek se objevil jednou, 4. dvakrát a tak dále.
tabulka, jako je tato, nám umožňuje znovu vytvořit realizaci bootstrapu mimo R.Nebo v samotném R, když nechceme použít set.seed a znovu provést celou komputaci.
onceAgain<-apply(tableOfIndices, 1, foo, data=iris, cor.type='s')pojďme zkontrolovat, zda jsou výsledky stejné:
Ano, jsou!
pokud se chcete dozvědět více o strojovém učení v R, absolvujte kurz nástrojů pro strojové učení DataCamp.