Hidden Markov Model: Jednoduchá Definice A Přehled

Statistiky Definice >

Hidden Markov Model (HMM) je relativně jednoduchý způsob, jak model sekvenční data. Skrytý Markovův model znamená, že Markovův Model, který je základem dat, je vám skrytý nebo Neznámý. Konkrétněji, znáte pouze pozorovací data a ne informace o státech. Jinými slovy, existuje specifický typ modelu, který produkuje data (Markovův Model), ale nevíte, jaké procesy je produkují. Jste v podstatě použít své znalosti z Markovovy Modely, aby se kvalifikovaný odhad o modelu konstrukce.

co je Markovův Model?

Chcete-li odhalit skrytý Markovův Model, musíte nejprve pochopit, co je Markovův Model. Zde vytvořím jednoduchý příklad pomocí dvou položek, které jsou velmi pravděpodobné: kostky a tašky barevných koulí.

model komponent, které budete používat k vytvoření náhodného modelu, jsou:

• šest-sided červené kostce.
• desetistranná Černá matrice.
• červený sáček s deseti kuličkami. Devět kuliček je červených, jedna je černá.
• černá taška s dvaceti kuličkami. Jeden míč je červený, devatenáct je černých.

„černá“ a „červená“ jsou dva stavy v tomto modelu(jinými slovy, můžete být černá, nebo můžete být červená).
nyní vytvořte model podle následujících kroků:

1. emisní krok: Roll matrice. Všimněte si čísla, které se objeví. To je emise. Ve výše uvedené grafice jsem si vybral červenou matrici, abych začal (libovolně – mohl jsem si vybrat černou) a válcoval 2.
2. přechodový krok: náhodně vyberte míč z vaku s barvou, která odpovídá matrici, kterou jste hodili v kroku 1. Válcoval jsem červenou matrici, takže si vyberu míč z červené tašky. Vytáhl jsem černou kouli, takže se chystám přejít na černou matrici pro další emise.

pak můžete tyto kroky opakovat na určitý počet emisí. Například opakování této posloupnosti kroků 10 krát vám může dát sadu {2,3,6,1,1,4,5,3,4,1}. Proces přechodu z jednoho stavu do druhého se nazývá Markovův proces.

přechod z červené na černou nebo černou na červenou nese různé pravděpodobnosti, protože v pytlích jsou různé počty černých a červených koulí. Následující diagram ukazuje pravděpodobnosti pro tento konkrétní model, který má dva stavy (černá a červená):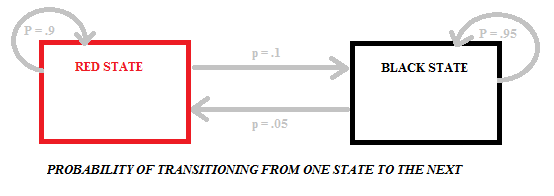

Hidden Markov Model Notace

λ = (A,B,π), je zkrácený zápis pro HMM. Další notace se používá u skrytých Markovových modelů:

• = státní pravděpodobnosti přechodu (aij)
• B = pozorování pravděpodobnostní matice (bj(k))
• N = počet stavů v modelu {1,2…, N}, nebo stavu, v čase t →st
• M = počet odlišných pozorování symboly na státní
• Q = {q0, q1, . . . , qN-1} = odlišné stavy Markovova procesu
• T = délka pozorovací sekvence
• V = {0, 1, . . . , M-1} = soubor možných pozorování
• O = (O0, O1, . . . , OT -1) = pozorování sekvence
• π = počáteční stav distribuce (ni)
• s = stav nebo posloupnost (s1, s2… sn)
• xk = skryté státu
• zk = pozorování.

Tři Základní Problémy,

Tři základní problémy mohou být vyřešeny s Skryté Markovovy Modely:

1. Vzhledem k Skryté Markovovy Modelλ = (A, B, π) a posloupnost pozorování O, najít pravděpodobnost, že pozorování P(O | λ). Tomu se někdy říká problém hodnocení.
2. vzhledem ke skrytému Markovovu modelu (A, B, π) a pozorovací sekvenci O Najděte nejpravděpodobnější stavovou sekvenci (s1, s2… sn). To se někdy nazývá problém dekódování.
3. Najít pozorovací sekvence (O1, O2…On a Hidden Markov Model λ = (A, B, π), který maximalizuje pravděpodobnost, že O To se někdy nazývá Problém s Učením nebo Optimalizační Problém.

Rabiner, L. R. „návod na skryté Markovovy modely a vybrané aplikace v rozpoznávání řeči“, Proceedings of the IEEE, vol.77, s. 257-286, Únor. 1989.
Razítko, M. (2013). Odhalující Úvod do skrytých Markovových modelů. Citováno 8/6/2013 z: http://www.cs.sjsu.edu/~stamp/RUA/HMM.pdf

——————————————————————————

Potřebujete pomoci s úkoly nebo zkoušky otázka? S Chegg Study, můžete získat krok za krokem řešení vašich otázek od odborníka v oboru. Váš první 30 minut s Chegg tutorem je zdarma!