Kruh je rovnoměrně rozdělen do šesti shodných trojúhelníků.

Ahoj Marilynn,

Nejdřív bych vám říct, že mé předpoklady o tom, co váš obraz vypadá:

1. Každý trojúhelník má vrchol (roh) ve středu kružnice,
2. Každý trojúhelník má rohy na obvodu kruhu (tak, dvě strany každého trojúhelníku je poloměr)
3. Trojúhelníky sdílet stranách (nejsou tam žádné hledí mezi trojúhelníky)

celkový obraz vypadá jako květina – každý trojúhelník je okvětní lístek.

neznámá oblast je to, co je ponecháno kolem vnější strany kruhu, mezi obvodem a vnější stranou každého trojúhelníku. Tato neznámá oblast je rozdělena do šesti shodných sekcí (stejně jako trojúhelníky jsou“ stejné “ ve všech směrech-včetně oblasti, délky strany a délky oblouku). Není jasné, zda máte na mysli oblast jednoho oblouku je Pí (ne vlastně rozdělit Koláč, i když pronouced stejné), nebo všech šest částí dohromady je Pí. V následujícím textu budu předpokládat, že jedna z vnějších částí má plochu Pi, takže plocha všech šesti úseků dohromady je 6 krát Pi. Musíme najít poloměr kruhu, nazývat to r.

budu také používat P jako stojan pro Pi (nebo cca. 3.14). Nyní je spousta informací, které můžeme ozdobit z trojúhelníků:

1. úhly ve středu jsou všechny 60 stupňů. Je to proto, že šest úhlů ve středu je stejné a kruh má 360 stupňů. Takže 360 edivided 6.
2. každý trojúhelník je rovnoramenný. Je to proto, že dvě strany jsou stejné (strany, které jsou poloměrem).
3. každý trojúhelník je ve skutečnosti rovnostranný. Protože se jedná o iscoceles, dva vnější úhly jsou také stejné. Ale v trojúhelníku je 180 stupňů, 60 se již používá ve středovém úhlu, takže 180-60=120 stupňů pro vnější úhly. Ale 120 děleno 2 je 60 stupňů, takže všechny tři úhly jsou stejné, takže jsou to isoscles.
4. každá strana v každém trojúhelníku má délku r. Je to proto, že máme 6 shodných („rovných“ ve všech směrech) rovnostranných trojúhelníků a protože dvě strany každého trojúhelníku jsou poloměr.

z geometrie trojúhelníků musíme udělat nějakou algebru. Protože známe oblast a potřebujeme poloměr, potřebujeme vzorec (nebo rovnici) pro poloměr z hlediska oblasti (v následujícím textu mějte na paměti cíl vzorce). Obsah kruhu je P*r2 (r2 znamená, že r na druhou, a * znamená násobení) oblast zbylé úseky mimo trojúhelníky, ale uvnitř kruhu (oblast, my už ne být 6*P), lze nalézt také odečtením plochy trojúhelníky z prostoru kruhu. Musíme najít oblast jednoho z rovnostranných trojúhelníků.

Metoda 1 pro výpočet plochy trojúhelníku
obsah trojúhelníku je b*h/2 To je místo, kde některé trigonometrie je potřeba: Nakreslete čáru z vrcholu na opačný straně, která dělí protější stranu v půl a je v pravém úhlu. To rozděluje rovnostranný trojúhelník na dva shodné pravoúhlými trojúhelníky, a nová strana je výška, volat to h. Musíme najít h.

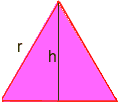
Pomocí trig v jednom z pravoúhlými trojúhelníky, máme sin60 = h/r, Ale sin60 = sqr(3)/2, kde sqr(3) znamená, že odmocnina ze tří, takže sqr(3)/2 = h/r vynásobíme obě strany rovnice, r, aby si h = r*sqr(3)/2 r Nyní, oblast jednoho rovnostranného trojúhelníku je b*h/2 = (r)*(r*sqr(3)/2)/2 = (r2)*sqr(3)/4 r = sqr(6*P/(P-6*sqr(3)/4)) Použití pořadí operací vypočítat na kalkulačce (s P=3.14): r= 5.896… Poloměr kruhu je tedy cca. 5.9. Pavel