použití logaritmů v reálném světě

logaritmy jsou všude. Použili jste někdy následující fráze?

• 6 údaje
• Dvojité číslice
• řádově
• Úroková sazba

popisuješ čísla, pokud jde o jejich pravomoci 10, logaritmus. A úroková sazba je logaritmem růstu investice.

překvapilo vás, že logaritmy jsou tak běžné? Já taky. Většina pokusů o Matematiky V Reálném Světě (TM) poukazují na logaritmu v nějaké tajemné formule, nebo předstírat, že jsme geologové fascinován Richterovy Stupnice. „Vědci se starají o protokoly a měli byste také. Také si dokážete představit svět bez zinku?“

Ne, ne, ne, ne ne, ne ne! (Mama mia!)

Matematika vyjadřuje pojmy s notací jako “ ln „nebo “ log“. Najít „matematiku v reálném světě“ znamená setkat se s myšlenkami v životě a vidět, jak by mohly být napsány s notací. Nehledejte doslovné symboly! Kdy jste naposledy napsal divizní ceduli? Kdy jste naposledy sekal nějaké jídlo?

Ok, ok, chápeme to: o čem jsou logaritmy?

logaritmy najdou příčinu efektu, tj. vstup pro nějaký výstup

běžný „efekt“ vidí něco růst, jako přechod z \$100 na \$150 za 5 let. Jak se to stalo? Nejsme si jisti, ale logaritmus najde možnou příčinu: nepřetržitý návrat ln (150/100) / 5 = 8,1% by představoval tuto změnu. Nemusí to být skutečná příčina (došlo v posledním roce k veškerému růstu?), ale je to hladký průměr, který můžeme srovnávat s jinými změnami.

mimochodem, pojem „příčina a následek“ je nuancí. Proč je 1000 větší než 100?

• 100 je 10, který vyrostl sám na 2 časová období ($10 * 10$)
• 1000 je 10, který vzrostl o sobě pro 3 časová období ($10 * 10 * 10$)

můžeme si čísla jako výstupy (1000 je „1000 výstupy“) a vstupy („kolikrát se 10 potřebují růst, aby se ty výstupy?“). Takže,

1000 outputs > 100 outputs

protože

3 inputs > 2 inputs

nebo jinými slovy:

log(1000) > log(100)

proč je to užitečné?

logaritmy uvádějí čísla na stupnici přátelskou k lidem.

velká čísla lámou naše mozky. Miliony a biliony jsou „opravdu velké“, i když milion sekund je 12 dní a bilion sekund je 30 000 let. Je to rozdíl mezi americkým prázdninovým rokem a celou lidskou civilizací.

trik k překonání „obrovské číslo slepota“ je psát čísla, pokud jde o „vstupy“ (tj. jejich power base 10). Toto menší měřítko (0 až 100) je mnohem snazší pochopit:

• moc 0 = $10^0$ = 1 (jednu položku)
• moc 1 = $10^1$ = 10
• napájení 3 = $10^3$ = tisíc
• napájení z 6 = $10^6$ = milionu
• výkon 9 = $10^9$ = miliard
• napájení z 12 = $10^12$ = bilionů
• výkon 23 = $10^23$ = počet molekul ve dvanáct gramů uhlíku,
• výkon 80 = $10^80$ = počet molekul ve vesmíru

0 na 80 měřítku nás vzal z jedné položky na počet věcí ve vesmíru. Ne příliš ošuntělý.

logaritmy počítají násobení jako kroky

logaritmy popisují změny z hlediska násobení: ve výše uvedených příkladech je každý krok 10x větší. U přirozeného protokolu je každý krok “ e “ (2.71828…) krát více.

při práci s řadou násobení logaritmy pomáhají „počítat“ je, stejně jako sčítání se počítá pro nás, když jsou přidány efekty.

Ukaž mi matematiku

čas na maso: uvidíme, kde se objeví logaritmy!

šestimístný plat nebo 2místný výdaj

popisujeme čísla z hlediska jejich číslic, tj. kolik pravomocí 10 mají (jsou v desítkách, stovkách, tisících, desetitisících atd.). Přidání číslice znamená „vynásobením 10“, tj.

Logaritmy spočítat počet násobení přidáno, tak začíná s 1 (jedna číslice) přidáme 5 více číslic ($10^5$) a 100 000 se 6-obrázek výsledku. Mluvit o“ 6 „místo“ sto tisíc “ je podstatou logaritmů. Dává hrubý smysl pro měřítko, aniž by skočil do detailů.

Bonusová otázka: jak byste popsal 500 000? Říkat „6 postava“ je zavádějící, protože 6-Čísla často znamená něco blíže k 100,000. Fungovalo by“ 6.5 číslo“?

opravdu ne. V našich hlavách 6.5 znamená „Na půli cesty“ mezi 6 a 7 čísly, ale to je myšlení zmije. S logaritmy a“.5 “ znamená polovinu z hlediska násobení, tj. druhá odmocnina ($9^.5$ znamená, že druhá odmocnina z 9 — 3 je v polovině násobení, protože je to 1 až 3 a 3 až 9).

Vezmeme-li protokol (500 000), dostaneme 5,7, přidáme 1 pro další číslici a můžeme říci “ 500 000 je 6.7 číslo obrázku“. Vyzkoušejte to zde:

řádová velikost

my geekové milujeme tuto frázi. To znamená zhruba „10x rozdíl“, ale jen zní chladnější než „1 číslice větší“.

v počítačích, kde se vše počítá s bity (1 nebo 0), má každý bit efekt zdvojnásobení (ne 10x). Takže jít z 8 na 16 bitů je „8 řádů“ nebo $ 2^8 = 256$ krát větší. („Větší“ v tomto případě označuje množství paměti, které lze řešit.) Přechod z 16 na 32 bitů znamená dalších 16 řádů, nebo $ 2^16 $ ~ 65,536 krát více paměti, kterou lze adresovat.

úrokové sazby

jak zjistíme tempo růstu? Země nemá v úmyslu růst na 8,56% ročně. Podíváte se na HDP jeden rok a HDP další, a vezměte logaritmus, abyste našli implicitní tempo růstu.

Moje dvě oblíbené interpretace přirozeného logaritmu (ln (x)), tj. 1.5:

• za předpokladu 100% růstu, jak dlouho potřebujete růst, abyste se dostali na 1,5? (.405, méně než polovina časového období)
• za předpokladu 1 jednotky času, jak rychle potřebujete růst, abyste se dostali na 1,5? (40.5% ročně, průběžně složené)

logaritmy jsou způsob, jak zjistíme, jak rychle rosteme.

měřítko měření: Google PageRank

Google dává každé stránce na webu skóre (PageRank), což je hrubá míra autority / důležitosti. Toto je logaritmická stupnice, což v mé hlavě znamená „PageRank počítá počet číslic ve vašem skóre“.

takže web s pagerank 2 („2 číslice“) je 10x populárnější než Web PageRank 1. Můj web je PageRank 5 a CNN má PageRank 9, takže je rozdíl 4 řády ($10^4$ = 10,000).

zhruba řečeno, mám asi 7000 návštěv / den. Pomocí mé obálky matematiku, mohu odhadnout CNN dostane asi 7000 * 10.000 = 70 milionů návštěv / den. (Jak jsem to udělal? V mé hlavě si myslím, že $7k * 10k = 70 * K * K = 70 * M$). Možná mají pár krát více, než že (100M, 200M), ale pravděpodobně ne až 700M.

Google zprostředkuje spoustu informací s velmi hrubou stupnici (1-10).

měřítko měření: Richter, Decibel atd.

povzdech. Jsme na typickém příkladu „logaritmů v reálném světě“: Richterova stupnice a Decibel. Cílem je umístit události, které se mohou drasticky lišit (zemětřesení) v jednom měřítku s malým rozsahem (obvykle 1 až 10). Stejně jako PageRank je každé zvýšení o 1 bod 10x zlepšením výkonu. Největší zemětřesení zaznamenané člověkem bylo 9,5; dopad na poloostrov Yucatán, který pravděpodobně způsobil vyhynutí dinosaurů, byl 13.

decibely jsou podobné, i když mohou být negativní. Zvuky mohou přecházet z intenzivně Tichého (pindrop) na extrémně hlasitý (letadlo) a náš mozek to všechno dokáže zpracovat. Ve skutečnosti, zvuk letadla motoru je miliony (miliardy, biliony) krát silnější než pindrop, a to je nepohodlné mít stupnici, která jde od 1 do triliony. Protokoly udržují vše v rozumném měřítku.

logaritmické grafy

často uvidíte položky vynesené na „stupnici protokolu“. V mé hlavě to znamená, že jedna strana počítá „počet číslic“ nebo „počet násobení“, nikoli samotnou hodnotu. Opět to pomáhá ukázat divoce se měnící události v jednom měřítku(od 1 do 10, ne od 1 do miliard).

Mooreův zákon je skvělým příkladem: zdvojnásobíme počet tranzistorů každých 18 měsíců (obrázek s laskavým svolením Wikipedia).

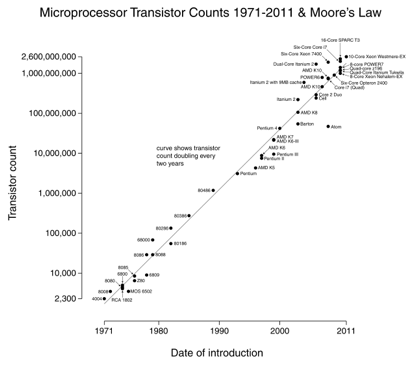
úhledná věc na grafech log-scale je, že exponenciální změny (rychlost procesoru) se objevují jako přímka. Pěstování 10x za rok znamená, že neustále pochodujete stupnicí“ číslic“.

kupředu a vzhůru

pokud je koncept dobře známý, ale není dobře milovaný, znamená to, že musíme budovat naši intuici. Najděte analogie, které fungují, a neuspokojte se s tím, že učebnice bude klusat. V mé hlavě:

• Logaritmu najít příčinu za účinek (viz růst, najít úroková sazba)
• pomáhají počítat, násobení nebo číslic, s bonusem dílčí počty (500k je 6.7 místné číslo)

Rádi matematiku.

Další Příspěvky V Této Sérii,

1. Intuitivní Průvodce Exponenciální Funkce & e
2. Demystifikací Přirozený Logaritmus (ln)
3. Vizuální Průvodce na Jednoduché, Složené a Kontinuální Úrokové Sazby
4. Společné Definice e (Obarvené)
5. Pochopení Exponenty (Proč 0^0 = 1?)
6. Pomocí Logaritmu v Reálném Světě
7. Jak to Myslíš S Exponenty A Logaritmy
8. Porozumění Diskrétní vs. Kontinuální Růst
9. Co exponentem vážně?
10. otázka: proč je e speciální? (2.718…, ne 2, 3.7 nebo jiné číslo?)