Rozdíl mezi IIR a FIR filtry: praktický design guide
digitální filtr je matematický algoritmus, který pracuje na digitální dataset (např. data snímače) s cílem získat informace o zájmu a odstranit nežádoucí informace. Aplikace tohoto typu technologie zahrnují odstranění závad z dat senzorů nebo dokonce vyčištění šumu na měřeném signálu pro snadnější analýzu dat. Ale jak si vybereme nejlepší typ digitálního filtru pro naši aplikaci? A jaké jsou rozdíly mezi filtrem IIR a filtrem FIR?
Digitální filtry jsou rozděleny do následujících dvou kategorií:
- Infinite impulse response (IIR)
- Finite impulse response (FIR)
Jak názvy napovídají, každý typ filtru je do kategorií podle délky impulsní odezvy. Před zahájením podrobné matematické analýzy je však rozumné ocenit rozdíly ve výkonu a vlastnostech každého typu filtru.
Příklad
pro ilustraci rozdíly mezi IIR a FIR, frekvenční odezva 14 pořadí JEDLE (plná čára) a 4. řádu Čebyševových Typu IIR (přerušovaná čára) je uveden níže na Obrázku 1. Všimněte si, že i když magnituda spektra mají podobný stupeň útlumu, fázové spektrum IIR filtr je to nelineární v propustného pásma (\(\small 0\rightarrow7.5 hz\)), a stane se velmi nelineární na cut-off frekvence, \(\small f_c=7.5 Hz\). Všimněte si také, že FIR vyžaduje vyšší počet koeficientů (15 vs 10 IIR), aby odpovídal útlumovým charakteristikám IIR.
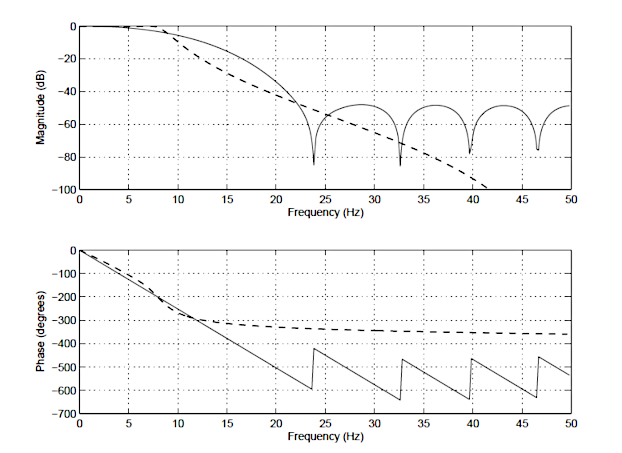
To jsou jen některé z rozdílů mezi těmito dvěma typy filtrů. Nyní bude následovat podrobné shrnutí hlavních výhod a nevýhod každého typu filtru.
filtry IIR
filtry IIR (infinite impulse response) se obecně volí pro aplikace, kde lineární fáze není příliš důležitá a paměť je omezená. Byly široce nasazeny v oblasti vyrovnávání zvuku, zpracování signálu biomedicínských senzorů, inteligentních senzorů IoT/IIoT a vysokorychlostních telekomunikačních / RF aplikací.
výhody
- nízké náklady na implementaci: vyžaduje méně koeficientů a paměti než FIR filtry, aby splňovaly podobnou sadu specifikací, tj.
- nízká latence: vhodné pro řízení v reálném čase a velmi vysokorychlostní RF aplikace díky nízkému počtu koeficientů.
- analogový ekvivalent: může být použit pro napodobování vlastností analogových filtrů pomocí transformací mapování roviny s-z.
nevýhody
- nelineární fázové charakteristiky: Fázové znaky filtru IIR jsou obecně nelineární, zejména v blízkosti mezních frekvencí. All-pass vyrovnávací filtry mohou být použity za účelem zlepšení charakteristik fáze průchodového pásma.
- podrobnější analýza: při implementaci v pevném bodě vyžaduje větší škálování a číselnou analýzu přetečení. Struktura filtru Direct form II je zvláště citlivá na účinky kvantizace a vyžaduje zvláštní péči během fáze návrhu.
- numerická stabilita: Méně numericky stabilní než jejich protějšky FIR (konečná impulsní odezva) kvůli zpětnovazebním cestám.
FIR filtry
FIR (finite impulse response) filtry jsou obvykle vybrány pro aplikace, kde lineární fáze je důležitá a slušné množství paměti a výpočetního výkonu jsou k dispozici. Mají široce nasazeny v audio a biomedicínských aplikací pro vylepšení signálu. Jejich nulová struktura (popsaná níže) zajišťuje, že se nikdy nestanou nestabilními pro jakýkoli typ vstupního signálu, což jim dává výraznou výhodu oproti IIR.
výhody
- lineární fáze: jedle mohou být snadno navrženy tak, aby měly lineární fázi. To znamená, že do signálu, který má být filtrován, není zavedeno žádné fázové zkreslení, protože všechny frekvence jsou posunuty v čase o stejné množství – čímž se zachovávají jejich relativní harmonické vztahy (tj. To rozhodně není případ IIR filtrů, které mají nelineární fázovou charakteristiku.
- stabilita: jako Fir nepoužívají předchozí výstupní hodnoty pro výpočet jejich současného výstupu, tj. nemají žádnou zpětnou vazbu, nikdy se nemohou stát nestabilními pro jakýkoli typ vstupního signálu,což jim dává výraznou výhodu oproti filtrům IIR.
- libovolná Frekvenční odezva: funkce firarb () Parks-McClellan a ASN FilterScript umožňuje návrh FIR s libovolnou odezvou velikosti. To znamená, že jedle lze přizpůsobit snadněji než IIR.
- výkon s pevným bodem: účinky kvantizace jsou méně závažné než účinky IIR.
nevýhody
- vysoký výpočetní a paměťový požadavek: Jedle obvykle vyžadují mnohem více koeficientů pro dosažení ostrého cut-off než jejich protějšky IIR. Důsledkem toho je, že vyžadují mnohem více paměti a výrazně vyšší množství operací MAC (vícenásobné a akumulační). Nicméně, moderní mikrokontrolér architektury založené na Arm Cortex M jader nyní zahrnují DSP hardwarové podpory přes SIMD (signál instrukce, více dat), že urychlení filtrování provozu výrazně.
- vyšší latence: vyšší počet koeficientů znamená, že FIR je obecně méně vhodný než IIR pro rychlé aplikace s vysokou propustností. To se stává problematickým pro řídicí aplikace s uzavřenou smyčkou v reálném čase, kde FIR filtr může mít příliš velké skupinové zpoždění, aby dosáhl stability smyčky.
- žádný analogový ekvivalent: pomocí bilineární, odpovídající Z-transformace (mapování s-z) lze analogový filtr snadno transformovat na ekvivalentní IIR filtr. To však není možné pro jedle, protože nemá analogový ekvivalent.
Matematické definice
, Jak je popsáno v úvodu, název IIR a FIR pocházejí z matematické definice každého typu filtru, tj. IIR filtr je zařazen do kategorie podle jeho teoreticky nekonečnou impulsní odezvou,
y(n)=\sum_{k=0}^{\infty}h(k)x(n-k)
\)
a JEDLE roztříděny podle jeho finite impulse response,
y(n)=\sum_{k=0}^{N-1}h(k)x(n-k)
\)
nyní Budeme analyzovat matematické vlastnosti každého typu filtru v pořadí.
IIR definice
Jak je vidět výše, IIR filtr je zařazen do kategorie podle jeho teoreticky nekonečnou impulsní odezvou,
\(\displaystyle y(n)=\sum_{k=0}^{\infty}h(k)x(n-k) \)
Prakticky vzato, to není možné vypočítat výstup IIR pomocí této rovnice. Proto může být rovnice přepsána z hlediska konečného počtu pólů \(\malý p\) a nul \(\malý q\), Jak je definováno lineární konstantním koeficientem diferenční rovnice daná:
y(n)=\sum_{k=0}^{q}b_k x(n-k)-\sum_{k=1}^{p}a_ky(n-k)
\)
kde \(\small a_k\) a \(\malý b_k\) filtr je jmenovatel a čitatele polynom koeficienty, kdo je kořeny jsou rovná filtr pólů a nul, resp. Tedy, vztah mezi diferenční rovnice a z-transformace (přenosovou funkci) může proto být definován pomocí z-transformace zpoždění majetku tak, že,
\sum_{k=0}^{q}b_kx(n-k)-\sum_{k=1}^{p}a_ky(n-k)\quad\stackrel{\displaystyle\mathcal{Z}}{\longleftrightarrow}\quad\frac{\sum\limits_{k=0}^q b_kz^{-k}}{1+\sum\limits_{k=1}^p a_kz^{-k}}
\)
Jak je vidět, funkce převodu je frekvenční doméně zastoupení filtr. Všimněte si také, že póly působí na výstupní data a nuly na vstupních datech. Protože póly působí na výstupní data a ovlivňují stabilitu, je nezbytné, aby jejich poloměry zůstaly uvnitř jednotkové kružnice (tj. <1) pro stabilitu BIBO (bounded input, bounded output). Poloměry nul jsou méně kritické, protože neovlivňují stabilitu filtru. To je hlavní důvod, proč jsou filtry all-zero FIR (konečná impulsní odezva) vždy stabilní.
BIBO stabilita
lineární časové invariantní (LTI) systém (např. digitální filtr) je řekl, aby byl ohraničený vstup, ohraničený výstup stabilní, nebo BIBO stabilní, jestliže každý ohraničený vstupní dává vzniknout ohraničené výstup, jako
\(\displaystyle \sum_{k=0}^{\infty}\left|h(k)\right|<\infty \)
, Kde \(\small h(k)\) je LTI systém je impulsní odezvy. Analýze této rovnice, mělo by být jasné, že BIBO stability, kritérium bude splněn, pokud systém je póly leží uvnitř jednotkové kružnice, protože systém je ROC (region of convergence) musí obsahovat jednotkové kružnice. V důsledku toho stačí říci, že ohraničený vstupní signál bude vždy produkovat ohraničený výstupní signál, pokud všechny póly leží uvnitř jednotkové kružnice.
nuly na druhé straně nejsou tímto požadavkem omezeny a v důsledku toho mohou ležet kdekoli na rovině z, protože přímo neovlivňují stabilitu systému. Proto, stabilita systému, může být analýza prováděná za prvé výpočet kořenů přenosové funkce (tj. kořeny čitatele a jmenovatele polynomy) a pak parcelování odpovídající póly a nuly na z-rovině.
zajímavá situace nastává, pokud na jednotkovém kruhu leží nějaké póly, protože se říká, že systém je okrajově stabilní, protože není stabilní ani nestabilní. Ačkoli marginálně stabilní systémy BIBO stabilní, byly využívány digitální oscilátor návrháři, protože jejich impulsní odezvy poskytuje jednoduchý způsob generování sinusové vlny, které se ukázaly jako neocenitelné v oblasti telekomunikací.
Biquad IIR filtry
IIR filtr provádění diskutovaných je řekl, aby byl biquad, protože má dva póly a dvě nuly, jak je znázorněno níže na Obrázku 2. Implementace biquad je zvláště užitečná pro implementace s pevným bodem, protože účinky kvantizace a numerické stability jsou minimalizovány. Nicméně, celkový úspěch jakékoli biquad realizace je závislá na dostupných číslo přesnost, která musí být dostatečná, aby bylo zajištěno, že kvantovaný póly jsou uvnitř jednotkové kružnice.
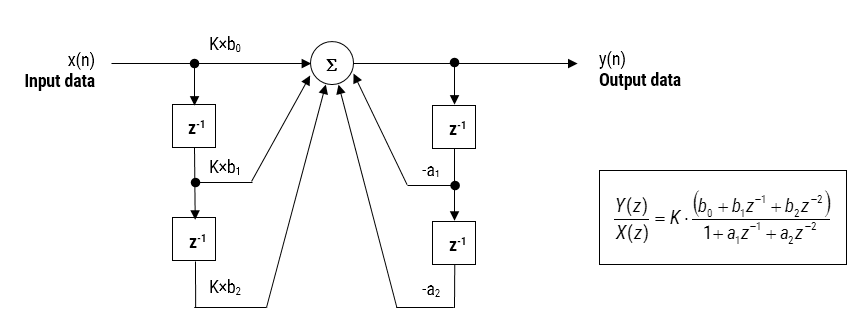
Obrázek 2: Přímá Forma I (biquad) IIR filtr realizace a přenosová funkce.
Analýze Obrázku 2, je vidět, že biquad struktura je ve skutečnosti skládá ze dvou zpětnou vazbu cesty (měřítko podle \(\small a_1\) a \(\small a_2\)), tři posuv cesty (měřítko podle \(\small b_0, b_1\) a \(\small b_2\)) a část zisku, \(\small K\). Filtrační operaci na obrázku 1 lze tedy shrnout následující jednoduchou rekurzivní rovnicí:
\(\displaystyle y(n)=K\times\Big – a_1 y(n-1)-a_2 y(n-2)\)
Analýza rovnice, všimněte si, že biquad provádění vyžaduje pouze čtyři dodatky (vyžadující pouze jednoho akumulátoru) a pět násobení, které lze snadno umístit na jakékoliv Cortex-M mikrokontroléru. Zisk sekce, \(\malý K\) může být před implementací také předem vynásoben koeficienty dopředné cesty.
kolekce filtrů Biquad je označována jako kaskáda Biquad, jak je znázorněno níže.

ASN Filter Designer může navrhnout a implementovat kaskádu až 50 biquads (Pouze Professional edition).
Floating point provádění
Při provádění filtr v plovoucí čárce (tzn. s použitím double nebo single precision arithmetic) Přímá Forma II struktury jsou považovány za lepší volby než Přímou Formu I strukturu. Přímá Forma II Transponovaná struktura je považována za nejvíce numericky přesné pro plovoucí desetinnou čárkou provádění, jako nežádoucí účinky numerické zaplavovat jsou minimalizovány jak je vidět z analýzy diferenčních rovnic.
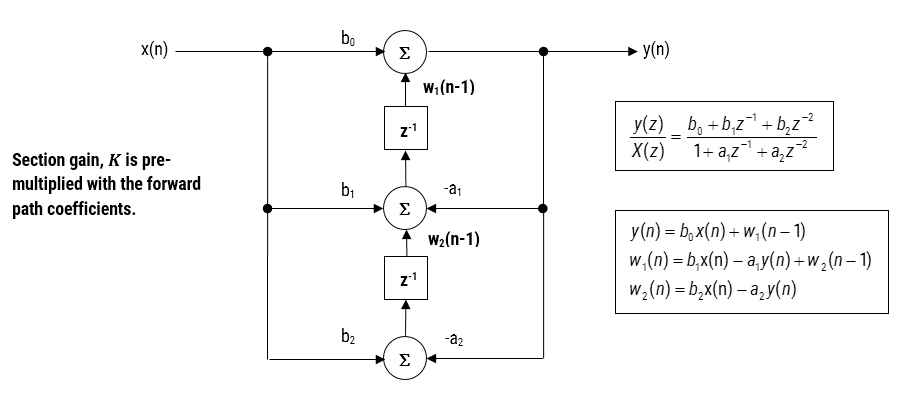
Obrázek 3 – Přímá Forma II je Provedena struktury, přenosu a diferenčních rovnic
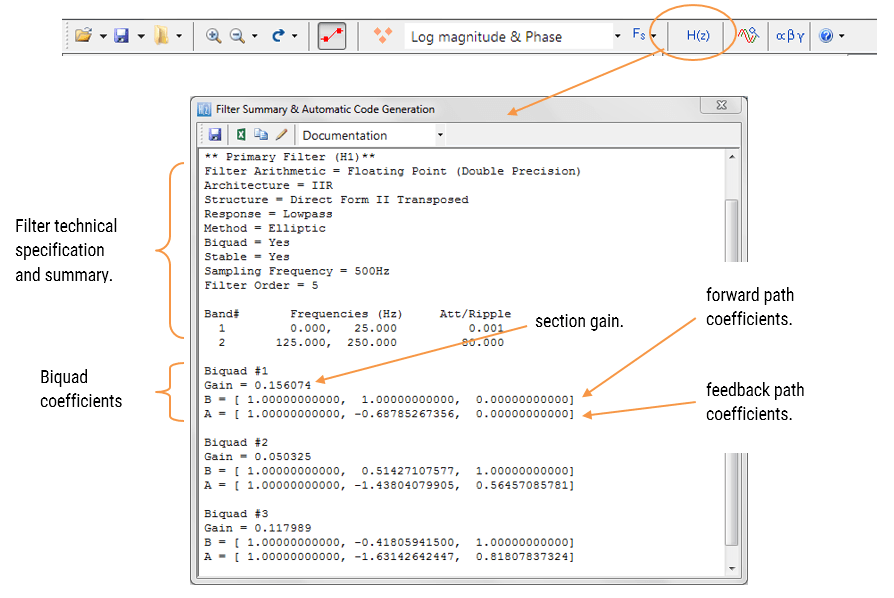
filtr shrnutí (znázorněno na Obrázku 4) poskytuje návrhář s detailní přehled navrženého filtru, včetně podrobný přehled technické specifikace a koeficientů filtru, který představuje rychlou a jednoduchou cestou k dokumentování vašeho návrhu.
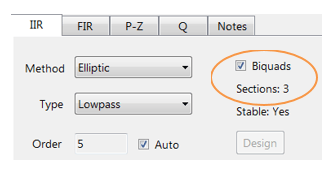
ASN Filter Designer podporuje návrh a implementaci IIR filtrů single section a Biquad (výchozí nastavení).
JEDLE definice
Vrací IIR lineární konstantní koeficient diferenční rovnice, tj.
y(n)=\sum_{k=0}^{q}b_kx(n-k)-\sum_{k=1}^{p}a_ky(n-k)
\)
Všimněte si, že když nastavíme \(\small a_k\) koeficienty (tj. zpětná vazba) na nulu, definice, snižuje se naše původní FIR filtr definice, což znamená, že JEDLE výpočet je založen pouze na minulost a současnost, vstupy hodnot, a to:
y(n)=\sum_{k=0}^{q}b_kx(n-k)
\)
Provádění
i když některé praktické implementace pro Jedlí existovat, přímá forma, struktura a jeho provedena bratranec jsou snad nejčastěji používají, a jako takový, všechny navrženy tak, filtrační koeficienty jsou určeny k provádění v Přímé formě struktury.
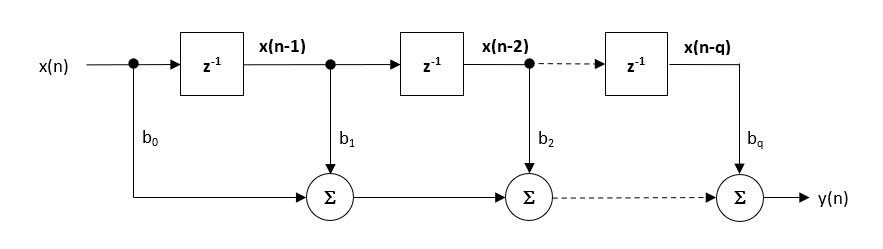
struktura přímé formy a související diferenční rovnice jsou uvedeny níže. Přímá forma je obhajována pro implementaci pevného bodu na základě konceptu jediného akumulátoru.
\(\displaystyle y(n) = b_0x(n) + b_1x(n-1) + b_2x(n-2) + …. +b_qx(n-q) \)
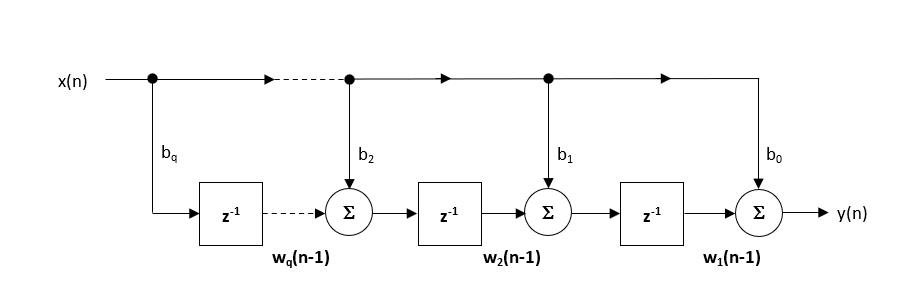
doporučené (default) struktura v rámci ASN Filter Designer je Přímá Forma Provedena struktury, jako to nabízí vynikající numerické přesnosti při použití plovoucí řádové čárce. To může být snadno vidět, a to prostřednictvím analýzy diferenčních rovnic níže (používá se pro provádění), jako nežádoucí účinky numerické zaplavovat jsou minimalizovány, protože floating point sčítání se provádí na čísla podobného rozsahu.
\(\displaystyle \begin{eqnarray}y(n) & = &b_0x(n) &+& w_1(n-1) \\ w_1(n)&=&b_1x(n) &+& w_2(n-1) \\ w_2(n)&=&b_2x(n) &+& w_3(n-1) \\ \vdots\quad &=& \quad\vdots &+&\quad\vdots \\ w_q(n)&=&b_qx(n) \end{eqnarray}\)
Co jsme se naučili?
digitální filtry jsou rozděleny do následujících dvou kategorií:
- Nekonečnou impulsní odezvou (IIR)
- Finite impulse response (FIR)
IIR (infinite impulse response) filtry jsou obvykle vybrány pro aplikace, kde je lineární fázi není příliš důležité, a paměť je omezená. Byly široce nasazeny v oblasti vyrovnávání zvuku, zpracování signálu biomedicínských senzorů, inteligentních senzorů IoT/IIoT a vysokorychlostních telekomunikačních / RF aplikací.
FIR (finite impulse response) filtry jsou obvykle vybrány pro aplikace, kde lineární fáze je důležitá a slušné množství paměti a výpočetního výkonu jsou k dispozici. Mají široce nasazeny v audio a biomedicínských aplikací pro vylepšení signálu.
ASN Filter Designer poskytuje inženýrům vše, co potřebují k návrhu, experimentování a nasazení komplexních digitálních filtrů IIR a FIR pro různé aplikace pro měření senzorů. Tyto výhody spolu s automatickou dokumentací a funkcí generování kódu umožňují technikům navrhnout a ověřit digitální filtr IIR/FIR během několika minut než hodin.
