Sluneční soustava: Země a Měsíc
planety jsou od nás vzdálené desítky a stovky milionů kilometrů. Aby se zabránilo použití tak velkých čísel, je astronomická jednotka (AU)přijata jako jednotka vzdálenosti, tj.Světlo trvá 8 minut a 19 sekund k pokrytí této vzdálenosti.
velikost sluneční soustavy přesahuje oběžnou dráhu Pluta při 40 AU A je definována jako ta, ve které se síla přitažlivosti slunce rovná síle přitažlivosti hvězd nejblíže k nám. Rozměry sluneční soustavy by pak byly řádově 1,5 105 AU. Je zřejmé, že tyto rozměry jsou velmi malé ve srovnání s rozměry galaxie nebo viditelného vesmíru. Jednotky, které jsou přijata opatření tyto obrovské vzdálenosti jsou světelného roku a parseku, že je ekvivalentní 206 265 AU nebo 3.26 světelných let.
planety sluneční soustavy jsou rozděleny do dvou skupin: pozemská skupina tvořená Merkurem, Venuší, zemí a Marsem a skupina obřích planet tvořená Jupiterem, Saturnem, Uranem a Neptunem.
všechny planety kromě Venuše a Merkuru mají satelity, z nichž většina patří k obřím planetám. Země, Jupiter, Saturn a Neptun mají největší satelity: Měsíc, satelity Jupiteru objevil Galileo (Io, Europa, Ganymede, Callisto), satelitní Titan Saturna a Neptuna Triton.
asteroidy zaujímají obrovskou prstencovou oblast mezi oběžnými drahami Marsu a Jupiteru v průměrné vzdálenosti 2,75 AU od Slunce. Největším asteroidem je Ceres, který má průměr 1000 km.
komety, kterých bylo katalogizováno asi 600, jsou rozděleny do dvou skupin, krátké období (do 20 let) a dlouhé období(přes 20 let). Existuje několik hypotéz o původu komet, včetně hypotézy nizozemského astronoma J. Oorta.
kromě orgánů uvedených v meziplanetární prostor, tam je velké množství částic různých velikostí, převážně ty s hmotností tisícin nebo miliontin gramu, které se nazývá hvězdný prach. Tvorba těchto částic je pravděpodobně způsobena kolizí větších těles (asteroidů) a jejich postupnou fragmentací po celou dobu existence a vývoje sluneční soustavy.
meteorický prach je zodpovědný za fenomén zodiakálního světla, který je pozorován po soumraku nebo před úsvitem v důsledku rozptylu světla těmito prachovými částicemi. Většina částic se odpařuje při vstupu do zemské atmosféry (ve výškách mezi 80 a 120 km), jen malá část dosahuje zemského povrchu.
teď se Pojďme podívat na některé údaje týkající se planety Sluneční Soustavy
První Slunce
| nebeské těleso | Rádio | Hmotnost |
|---|---|---|
| Slunce | 6.96·108 m | 1.98·1030 kg |
Pak ze Země
| nebeské těleso | poloosa | Období | Hmotnost |
|---|---|---|---|
| Země, | 149.6·109 m | 1 rok=365.26 dny | 5.98·1024 kg |
a zbytek planety
| Planeta | poloosa (AU) | Výstřednost | Období (roky) | Hmotnost |
|---|---|---|---|---|
| Rtuť | 0.387 | 0.206 | 0.24 | 0.06 |
| Venuše | 0.723 | 0.007 | 0.62 | 0.82 |
| Země | 1.000 | 0.017 | 1.00 | 1.00 |
| Mars | 1.524 | 0.093 | 1.88 | 0.11 |
| Jupiter | 5.203 | 0.048 | 11.86 | 318 |
| Saturn | 9.539 | 0.056 | 29.46 | 95.1 |
| Uran | 19.182 | 0.047 | 84.01 | 14.6 |
| Neptun | 30.058 | 0.009 | 164.8 | 17.2 |
V následující tabulce jsou uvedeny jako doplňující údaje:
- sklon roviny oběžné dráhy planety vůči ekliptice (rovině oběžné dráhy Země)
- doba rotace kolem své osy. Bylo velmi obtížné měřit tuto velikost pro planety jako Merkur a Venuše. Plynné skořápky Jupitera, Saturnu, Uranu a Neptunu mají vlastnost diferenciální rotace, to znamená, že jejich rotační periody se liší podle zeměpisné šířky.
- sklon osy otáčení vzhledem k rovině oběžné dráhy. V případě Venuše je 177º což je ekvivalentní říká, že sklon osy je 3º, ale směr otáčení je inverzní. Stejný argument platí pro Uran, což naznačuje, že osa otáčení Uranu je téměř v rovině jeho oběžné dráhy.
| Planeta | Sklon oběžné dráhy, | střídání Období | Hustota g/cm3 | Rádio rovníku (km) | osy Tilt | Ne. satelitů |
|---|---|---|---|---|---|---|
| Merkur | 7.0 | 58d.6 | 5.44 | 2 439 | <30º | 0 |
| Venuše | 3.4 | 243d | 5.24 | 6 051 | 177 ° | 0 |
| Země | 0 | 23h.9 | 5.52 | 6 378 | 23.5 | 1 |
| Mars | 1.8 | 24h.6 | 3.95 | 3 394 | 25º.2 | 2 |
| Jupiter | 1.3 | 9h.9 | 1.33 | 71 398 | 3.1 | 16 |
| Saturn | 2.5 | 10h.2 | 0.69 | 60 000 | 26º.4 | 17 |
| Uran | 0º.8 | 10h.8 | 1.26 | 25 400 | 98º | 5 |
| Neptun | 1.8 | 15h.8 | 1.67 | 24 750 | 29º | 2 |
satelity
nakonec poskytujeme některé údaje týkající se hlavních satelitů planet. Jupiter a Saturn mají mnoho satelitů, které jsou mnohem větší než Mars, ale budeme zmínit jen ty, které jsou podobné ve velikosti, nebo větší než náš Měsíc.
| Planeta | Satelity | Hustota g/cm3 | střední Poloměr (km) | Rádio oběžné dráze (103 km) | Období (dny) |
|---|---|---|---|---|---|
| Země, | Měsíc | 3.33 | 1 738 | 384.4 | 27.32 |
| Mars | Phobos | 2.1 | 13.5 | 9.38 | 0.319 |
| Deimos | 2.1 | 7.5 | 23.46 | 1.262 | |
| Jupiter | Io | 3.53 | 1 820 | 421.6 | 1.769 |
| Evropa | 3.03 | 1 565 | 670.9 | 3.551 | |
| Ganymede | 1.93 | 2 638 | 1 070 | 7.155 | |
| Calisto | 1.83 | 2 410 | 1 880 | 16.689 | |
| Saturn | Titan | 1.9 | 2 575 | 1 221.9 | 15.95 |
| Neptun | Newt | 2 200 | 394.7 | 5.84 |
aktivity
- určují hmotnost planety Jupiter z rádiových dat a období revoluce jednoho z jejích satelitů.
- Určit poloměr oběžné dráhy družice planety Jupiter z hmotnosti planety a doba oběhu družice.
- Určit intenzitu gravitačního pole g na povrchu planety a některé satelity, z údajů o jejich hmotnosti M a jejich poloměr R nebo jejich hustota ρ a jejich poloměr.
Příklad: určete hmotnost planety Jupiter s vědomím, že poloměr měsíce Io je 421,600 km a jeho doba oběhu je 1,769 dní. Skutečnost: konstanta G je 6.67 * 10-11 Nm2 / kg2
příklad: Vypočítejte poloměr oběžné dráhy satelitu Callisto s vědomím, že její doba oběhu je 16.689 dní a hmotnost planety Jupiter je 1.901·1027 kg. Data: konstanta G je 6.67 * 10-11 Nm2/kg2
g=G M R2 = 4π 3 GpR
Data: konstanta G je 6.67 * 10-11 Nm2 / kg2
Měsíc
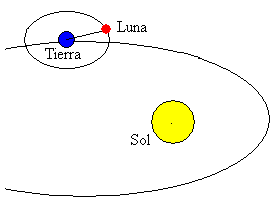
Měsíc je jedním z největších těles ve Sluneční soustavě. Jeho oběžná dráha je téměř kruhová (excentricita ε=0,05) a rovina její oběžné dráhy je nakloněna 5 ° vzhledem k rovině oběžné dráhy Země.
průměrná vzdálenost mezi středem Země a Měsícem je 384 400 km.Jeho doba rotace kolem Země je 27 322 dní. Změna polohy měsíce vzhledem ke slunci vede k fázím měsíce.
měsíc vždy představuje stejnou tvář pozemskému pozorovateli kvůli vlivu přílivových sil, které země působí na Měsíc. Což znamená, že doba rotace Měsíce kolem jeho osy se shoduje s časem potřebným k dokončení oběžné dráhy kolem Země.
měsíc je nebeský objekt, který nejvíce fascinoval lidský druh. Bývalý Sovětský svaz nejprve vyslal automatickou loď, která přistála na povrchu Měsíce v roce 1959. 20. července 1969 byli Neil Armstrong v doprovodu Edwina Aldrina prvními muži, kteří chodili na povrch Měsíce v rámci mise Apollo 11. Poslední návštěva amerických astronautů na Měsíci se konala v roce 1972.
původ měsíce se zdá nejistý, existuje několik teorií:
-
byla vytvořena ve stejné době Země s materiálem z mlhoviny
-
nebeské těleso je rozdělena do dvou částí, což vede k Zemi a Měsíc
-
to, Že Měsíc vznikl někde jinde a byl zajat Zemi
-
Že Země se srazil s nebeský objekt velkých rozměrů (o velikosti Marsu či větší), a že Měsíc byl vytvořen s materiálem vyloučen z této kolize.
druhá teorie se v současné době jeví jako nejuznávanější vědeckou komunitou.
měsíční cesta
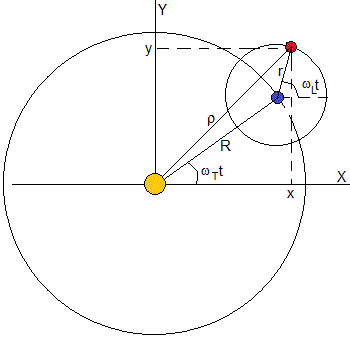
zvažte planetu a její satelit. Planeta popisuje kruhovou oběžnou dráhu o poloměru R kolem své hvězdy s konstantní úhlovou rychlostí wT=2π / PT, přičemž PT je období nebo čas, který vede k úplnému otočení. Satelitní popisuje kruhové dráze coplanaria o poloměru r s konstantní úhlovou rychlostí wL=2π/PL, že PL období nebo času je potřeba provést kompletní revoluci
pozice satelitu s ohledem na referenční systém jehož původ je hvězda,
x=Rcos( ω T )+rcos( ω L t ) y=Risiko( ω T )+risiko( ω L t )
Je α=wT/wL
{ x=Rcos( α ω L t )+rcos( ω L t ) y=Risiko( α ω L t )+risiko( ω L t ) { x=Rcos( α 2π P L t )+rcos( 2π P L t ) y=Risiko( α 2π P L t )+risiko( 2π P L t )
budeme Říkat τ=t/PL
x R =cos( α·2πτ )+ r r cos( 2πτ ) a R =sin( α·2πτ )+ r r sin( 2πτ )
Zastupujeme trajektorie družice pro α=0,1 a pro tři hodnoty poměru r/R
- r/R<α. Příklad, r / R=0,05
- r / R=α. Příklad, r / R=0,1
- r / R >α. Příklad, r / R=0.15
alfa=0.1;r=0.15;fplot(@(t) r*cos(2*pi*t)+cos(2*pi*alfa*t), @(t) r*sin(2*pi*t)+sin(2*pi*alfa*t),)text(0.1,0.1,sprintf('\alpha=%1.2f',alfa))text(0.1,0.2,sprintf('r/R=%1.2f',r))axis equalgrid onxlabel('x/R')ylabel('y/R')title('Trayectoria de un satélite')
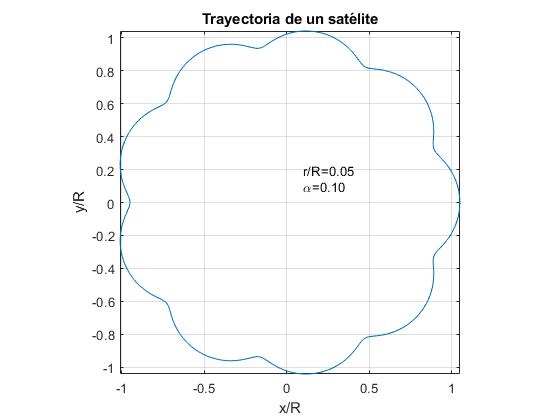
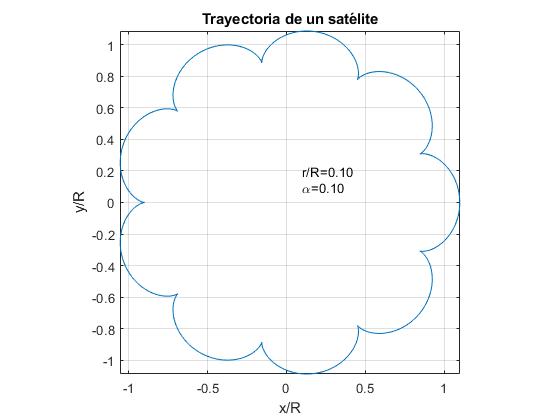
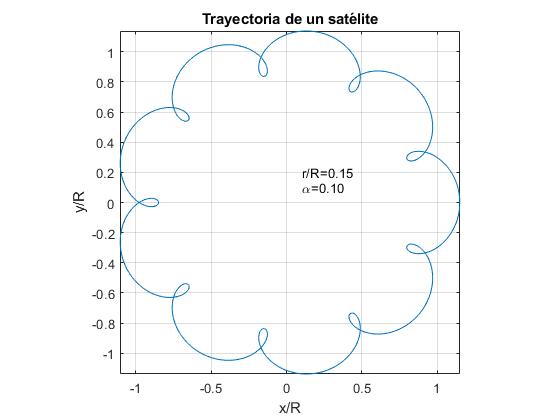
Pro případ, že Země a Měsíc jsou údaje:
- poloměr oběžné dráze Měsíce: r=384.4·106 m, období PL = 27.32 d
- poloměr oběžné dráhy Země: R = 149,6 * 109 m, perioda PT = 365,26 d
α=wT / wL=PL / PT=0,0748. r / R=0,0026
oběžná dráha Měsíce se bude podobat prvnímu číslu. V grafickém znázornění trajektorie Měsíce pro tyto hodnoty α a r/R neváží kolísání radiální vzdálenost mezi Slunce a Měsíc
Zrychlení na Měsíci
vzdálenost ρ od Slunce k Měsíci,
ρ 2 = x 2 + y 2 = R 2 + r 2 +2rRcos( ( ω L − ω T), t )
můžeme Vypočítat pravoúhlé složky zrychlení
{ dx dt =− ω T Risiko( ω T )− ω L risiko( ω L t ) dy dt = ω T Rcos( ω T )+ ω L rcos( ω L t ) { x = d 2 x d t 2 =− ω T 2 Rcos( ω T )− ω L 2 rcos( ω L t ) y = d 2 y d t 2 =− ω T 2 Risiko( ω T )− ω L 2 risiko( ω L t )
radiální složku zrychlení
ρ = a → · ρ → ρ = x x+ y x 2 + y 2 =− ω T 2 R 2 + ω L 2 r 2 +( ω T 2 + ω L 2 )Rrcos( ( ω L − ω T), t ) R 2 + r 2 +2 rr cos( ( ω L − ω T), t )
minimální a maximální hodnoty jsou získány, když cos((wL-wT)t)=±1
max =− ω T 2 R 2 + ω L 2 r 2 +( ω T 2 + ω L 2 )Rr R 2 + r 2 +2 rr =−( ω T 2 R+ ω L 2 r ) min =− ω T 2 R 2 + ω L 2 r 2 −( ω T 2 + ω L 2 )Rr R 2 + r 2 -2 rr =−( ω T 2 R− ω L 2 r )
>> R=149.6e9; %Tierra>> r=384.4e3; %Luna>> wT=2*pi/(365*24*60*60) %velocidad angular TierrawT = 1.9924e-07>> wL=2*pi/(27.32*24*60*60) %velocidad angular TierrawL = 2.6619e-06>> aM=-(wT^2*R+wL^2*r)aM = -0.0059>> am=-(wT^2*R-wL^2*r)am = -0.0059
Měsíc je jediný satelit ve Sluneční Soustavě, jejichž radiální složka zrychlení je záporné, to je říkal, že Měsíc padá směrem ke Slunci,‘
fáze Měsíce
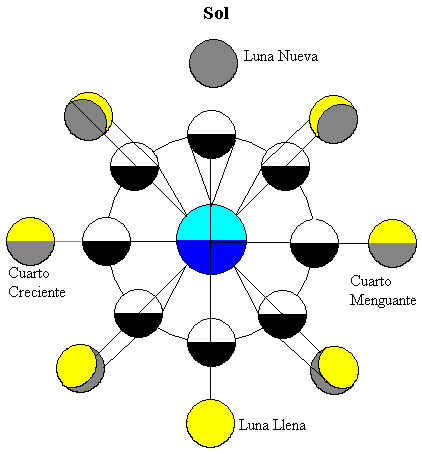
Na obrázku je Měsíc v různých polohách na své dráze kolem Země. Slunce je daleko svítící obou nebeských těles (v horní části obrázku)
Půl Měsíce je osvětlena Sluncem (v bílé barvě) a půl Měsíce nejblíže k Zemi, je vidět pozemní pozorovatele. Jak se Měsíc pohybuje kolem Země, vidíme různé zlomky části osvětlené sluncem (žluté oblasti).
-
Když Měsíc je mezi zemí a Sluncem, část Měsíc nejblíže k Zemi, je tma, takže nemůžeme vidět Měsíc, tato fáze se nazývá New Moon.
-
Když Země je mezi Sluncem a Měsícem, část Měsíc nejblíže k Zemi, je osvětlená polovina, tato fáze se nazývá úplněk.
-
když je Měsíc v mezilehlých polohách, je osvětlena pouze polovina nejbližší části země. Proto vidíme pouze čtvrtinu měsíce, tyto dvě fáze se nazývají čtvrtiny, které se zvyšují nebo snižují v závislosti na tom, zda osvětlená část viditelná ze země má tendenci růst nebo klesat.
Poznámka: Tento interaktivní program se snaží vysvětlit fáze Měsíce, ale to je věrný reprezentace z oběžné dráhy Měsíce, které svírají úhel 5 ° k rovině ekliptiky (Zemské dráhy kolem Slunce), nebo orientace osy Země, což je o 23º s kolmicí k rovině ekliptiky.
červená čára byla vedoucí přes Měsíc, takže čtenář může ocenit náhoda doby rotace Měsíce kolem své osy a čas potřebný k dokončení oběžné dráze kolem Země, a proto Měsíc má vždy stejnou tváří k Zemi.
zatmění Měsíce
zatmění Měsíce nastává vždy, když je Měsíc v plné fázi a kdykoli jsou Slunce, Země a Měsíc v přímce. Pak je měsíc ve stínu produkovaném zemí, jak je znázorněno na obrázku.
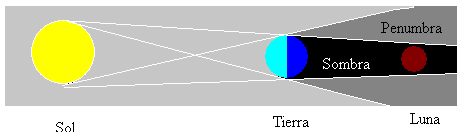
existují i jiné typy zatmění měsíce, které závisí na vyrovnání tří nebeských těles. Měsíc může být v neosvětlené oblasti (stín) nebo částečně osvětlené (penumbra).
zatmění Slunce nastane, když měsíc stojí mezi Sluncem a zemí, měsíc je v nové fázi. Měsíc je 400krát menší než Slunce, ale Měsíc je 400krát blíže zemi, takže zdánlivá velikost obou těles viděných ze země je téměř stejná. Měsíc tak může způsobit úplné zatmění Slunce, pokud je pozorován ve stínové zóně promítané měsícem na Zemi.
Měsíc Dat
| Hmotnost (v kg) | 7.349·1022 |
| Poloměr (km) | 1737. 4 |
| průměrná hustota (g/cm3) | 3.34 |
| průměrná Vzdálenost od Země (km) | 384 000 |
| Období oběžné dráze (dny) | 27.32166 |
| gravitační Zrychlení na rovníku (m/s2) | 1.62 |
| Excentricita oběžné dráhy | 0.0549 |
| Sklon oběžné dráhy (stupňů) | 5.1454 |
-
Vypočítejte poloměr kruhové oběžné dráhy Měsíce kolem Země s vědomím, že doba je 27.32 dnů. Vypočítejte také rychlost měsíce. Data: G =6,67 * 10-11 Nm2 / kg2, hmotnost Země je M=5,98 * 1024 kg.
-
Vypočítejte zrychlení gravitace g na povrchu Měsíce.
-
Vypočítejte kvocient mezi průměrem slunce a průměrem měsíce. Vypočítejte poměr mezi průměrnou vzdáleností mezi Sluncem a zemí a Měsícem a zemí. Údaje: poloměr Slunce 6.96 * 108 m, vzdálenost Středozem-sluncem 1.49 * 1011 m
-
Vypočítejte polohu těžiště systému Země-Měsíc, měřeno od středu Země.
-
Vypočítejte sílu přitažlivosti Země na Měsíci, porovnejte ji se silou přitažlivosti slunce na Měsíci. Datum: hmotnost Slunce, 1,98 * 1030 kg
odkazy
m. Marov. Planety sluneční soustavy. Nakladatelství Mir.
další informace o planetách kolik planet je v naší sluneční soustavě?. ComofuncionaQue.com
pro sekci „trajektorie měsíce“
David C.Johnston. Cykloidní dráhy ve fyzice jako superpozice translačních a rotačních pohybů. Rána. J.Phys.808-810
měsíc se vždy otáčí směrem ke Slunci. Matematické stránky.