Bootstrap in R

Bootstrap ist eine Methode zur Inferenz über eine Population unter Verwendung von Beispieldaten.Bradley Efron hat es zuerst in diesem eingeführtpapier im Jahr 1979.Bootstrap basiert auf Sampling mit Ersatz aus Beispieldaten. Diese Technik kann verwendet werden, um den Standardfehler jeder Statistik abzuschätzen und ein Konfidenzintervall (CI) dafür zu erhalten. Bootstrap ist besonders nützlich,wenn CI keine geschlossene oder sehr komplizierte Form hat.

Angenommen, wir haben eine Stichprobe von n Elementen:X = {x1, x2, …, xn} und wir interessieren uns für CI für eine Statistik T = t(X) . Bootstrapframework ist unkompliziert. Wir wiederholen einfach R mal das folgende Schema: Für i-te Wiederholung, Probe mit Ersatz n Elemente aus demverfügbare Probe (einige von ihnen werden mehr als einmal ausgewählt). Rufen Sie thisnew Probe i-te Bootstrap Probe, Xi, und calculatedesired Statistik Ti = t(Xi).

Als Ergebnis erhalten wir R Werte unserer Statistik:T1, T2, …, TR. Wir nennen sie Bootstrap-Realisierungen von T oder eine Bootstrap-Verteilung von T.Basierend darauf können wir CI für T berechnen. Die Einnahme von Perzentilen scheint die einfachste zu sein.

Bootstrap in Aktion

Verwenden wir (noch einmal) den bekannten iris -Datensatz. Schauen Sie sich ein paar Zeilen an:

Angenommen, wir möchten CIs für Median Sepal.Length, Median Sepal.Width und Spearmans Rangkorrelationskoeffizienten zwischen diesen beiden finden. Wir verwenden R ’s boot Paket und eine Funktion namens… boot. Um seine Leistung zu nutzen, müssen wir eine Funktion erstellen, die unsere Statistiken aus neu abgetasteten Daten berechnet. Es sollte mindestens zwei Argumente enthalten: einen dataset und einen Vektor mit indices Elementen aus einem Dataset, die zum Erstellen eines Bootstrap-Beispiels ausgewählt wurden.

Wenn wir CIs für mehr als eine Statistik gleichzeitig berechnen möchten, muss ourfunction sie als einzelnen Vektor zurückgeben.

In unserem Beispiel könnte es so aussehen:

library(boot)foo <- function(data, indices){ dt<-data c( cor(dt, dt, method='s'), median(dt), median(dt) )}

foo wählt die gewünschten Elemente (deren Zahlen in indices gespeichert sind) aus data aus und berechnet den Korrelationskoeffizienten der ersten beiden Spalten (method='s' wird verwendet, um den Rangkoeffizienten von Spearman auszuwählen, method='p' ergibt den Pearson-Koeffizienten) und deren Mediane.

Wir können auch einige zusätzliche Argumente hinzufügen, z. lassen sie benutzer wählen typ odcorrelation koeffizienten:

foo <- function(data, indices, cor.type){ dt<-data c( cor(dt, dt, method=cor.type), median(dt), median(dt) )}

Um dieses Tutorial allgemeiner zu gestalten, verwende ich die letztere Version vonfoo.

Jetzt können wir die Funktion boot verwenden. Wir müssen es mit einem Namen oddataset , einer Funktion, die wir gerade erstellt haben, einer Anzahl von Wiederholungen (R) und zusätzlichen Argumenten unserer Funktion (wie cor.type) versehen. Unten verwende ich set.seed für die Reproduzierbarkeit dieses Beispiels.

set.seed(12345)myBootstrap <- boot(iris, foo, R=1000, cor.type='s')

boot funktion gibt ein Objekt der aufgerufenen Klasse zurück… (ja, du hast recht!)boot. Es hat zwei interessante Elemente. $t enthält R-Werte unserer Statistik (en), die von der Bootstrap-Prozedur generiert wurden (Bootstrap-Realisierungen oft):

$t0 enthält Werte unserer Statistik(en) im Original, vollständig, Datensatz:

myBootstrap$t0## -0.1667777 5.8000000 3.0000000

Drucken boot Objekt an die Konsole gibt einige weitere Informationen:

original ist das gleiche wie $t0. bias ist eine Differenz zwischen dem Mittelwert der Bootstrap-Realisierungen (die von $t ), die als Bootstrap-Schätzung von T bezeichnet werden, und dem Wert im ursprünglichen Datensatz (der von $t0).

colMeans(myBootstrap$t)-myBootstrap$t0## 0.002546391 -0.013350000 0.007900000

std. error ist ein Standardfehler der Bootstrap-Schätzung, der gleich Iststandardabweichung von Bootstrap-Realisierungen.

apply(myBootstrap$t,2,sd)## 0.07573983 0.10295571 0.02726414

Verschiedene Arten von Bootstrap CIs

Bevor wir mit CI beginnen, lohnt es sich immer, einen Blick auf dieverteilung von Bootstrap-Realisierungen. Wir können die Funktion plot verwenden, wobeiindex angibt, welche der in foo berechneten Statistiken wir anzeigen möchten. Hier ist index=1 ein Spearman-Korrelationskoeffizient zwischensepallänge und -breite, index=2 ist eine mittlere Od-Sepallänge undindex=3 ist eine mittlere Od-Sepalbreite.

plot(myBootstrap, index=1)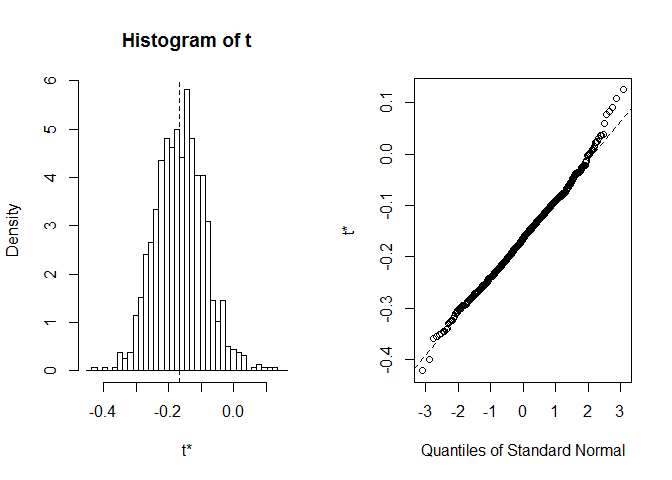

Die Verteilung der Bootstrap-Korrelationskoeffizienten scheint ziemlichnormal. Lass uns CI dafür finden. Wir können boot.ci verwenden. Der Standardwert ist 95 Prozent CIs, kann aber mit dem Parameter conf geändert werden.

boot.ci bietet 5 Arten von Bootstrap-CIs. Einer von ihnen, studentizedinterval, ist einzigartig. Es benötigt eine Schätzung der Bootstrap-Varianz. Wir stellen es nicht zur Verfügung, daher gibt R eine Warnung aus:bootstrap variances needed for studentized intervals . Varianzschätzungen können mit Bootstrap der zweiten Ebene oder (einfacher) Mitjackknife-Technik erhalten werden. Dies geht irgendwie über den Rahmen dieses Tutorials hinaus,also konzentrieren wir uns auf die verbleibenden vier Arten von Bootstrap-CIs.

Wenn wir sie nicht alle sehen wollen, können wir relevante im Argument type auswählen. Mögliche Werte sind norm, basic, stud, perc, bca ora Vektor von diesen.

Die Funktion boot.ci erstellt ein Objekt der Klasse… (ja, Sie haben es erraten!)bootci. Seine Elemente werden genau wie Typen von CI aufgerufen, die im Argument type verwendet werden. $norm ist ein 3-Element-Vektor, der Konfidenzlevel und CI-Grenzen enthält.

boot.ci(myBootstrap, index=1, type='norm')$norm## conf ## 0.95 -0.3177714 -0.02087672

$basic, $stud, $perc und $bca sind 5-Element-Vektoren, die auch Perzentile enthalten, die zur Berechnung von CI verwendet werden (wir werden später darauf zurückkommen):

boot.ci(myBootstrap, index=1, type='basic')$basic## conf ## 0.95 975.98 25.03 -0.3211981 -0.03285178

Ein bisschen Notation (Sorry!)

Um ein Gefühl dafür zu bekommen, was verschiedene Arten von CI sind, müssen wir einführeneine Notation. Also, lass:

• t⋆ sei die Bootstrap−Schätzung (Mittelwert der Bootstraprealisierungen),
• t0 sei ein Wert unserer Statistik im ursprünglichen Datensatz,
• se⋆ sei ein Standardfehler der Bootstrap-Schätzung,
• b sei eine Verzerrung der Bootstrap-Schätzungb = t⋆ – t0
• α ein Konfidenzniveau sein, typischerweise α = 0,95,
• za ein $ 1- \ frac \alpha 2 $ -Quantil der Standardnormalverteilung sein,
• θα ein α-Perzentil der Verteilung von Bootstraprealisierungen sein.

Perzentil-CI

Mit der obigen Notation ist Perzentil-CI:

(θ(1 – α)/2, θ1 − (1 – α)/2)

dies erfordert also nur relevante Perzentile. Nichts weiter.

Normales KI

Ein typisches Wald-KI wäre:

t0 ± za ⋅ se⋆

aber im Bootstrap-Fall sollten wir es für Bias korrigieren. So wird es:

$$ t_0 – b \pm z_\alpha \cdot se^\star \\ 2t_0 – t^\star \pm z_\alpha \cdot se^\star $$

Basic CI

Perzentil CI wird im Allgemeinen nicht empfohlen, da es schlecht abschneidet, wenn es um Verteilungen mit seltsamem Schwanz geht. Grundlegendes CI (auch genanntpivotales oder empirisches CI) ist dazu viel robuster. Das Rationale dahinter ist, Unterschiede zwischen jeder Bootstrap-Replikation und t0 zu berechnen und Perzentile ihrer Verteilung zu verwenden. Vollständige Details finden Sie z. B. in L. Wassermans All ofStatistics

Die endgültige Formel für das grundlegende CI lautet:

(2t0 − θ1 − (1 − α) / 2, 2t0 − θ(1 – α)/2)

BCa CI

BCa kommt von Bias-korrigiert, beschleunigt. Die Formel dafür ist nicht sehr kompliziert, aber etwas unintuitiv, also werde ich es überspringen.Siehe Artikel von Thomas J. DiCiccio und BradleyEfron, wenn Sie an Details interessiert sind.

Die im Methodennamen erwähnte Beschleunigung erfordert die Verwendung von specificpercentiles von Bootstrap-Realisierungen. Manchmal kann es vorkommen, dassDies wären einige extreme Perzentile, möglicherweise Ausreißer.BCa kann in solchen Fällen instabil sein.

Betrachten wir den BCa-CI für den Median der Blütenblattbreite. Im ursprünglichen Datensatz entspricht dieser Median genau 3.

Wir erhalten BCa CI (2.9, 2.9). Das ist seltsam, aber zum Glück Rwarnte uns, dass extreme order statistics used as endpoints. Mal sehenwas genau hier passiert ist:

plot(myBootstrap, index=3)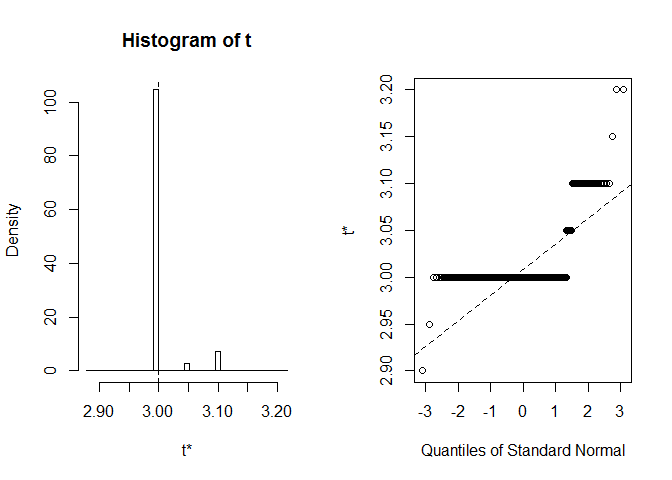

Die Verteilung von Bootstrap-Realisierungen ist ungewöhnlich. Eine große Mehrheit von ihnen (über 90%) sind 3s.

table(myBootstrap$t)#### 2.9 2.95 3 3.05 3.1 3.15 3.2## 1 1 908 24 63 1 2

Replikation der Ergebnisse

Manchmal müssen wir Bootstrap-Replikationen neu erstellen. Wenn wir Rdafür verwenden können, ist dies kein Problem. set.seed Funktion löst das Problem.Das Wiederherstellen von Bootstrap-Replikationen in anderer Software wäre viel mehrkompliziert. Darüber hinaus kann für große R die Neuberechnung in R ebenfalls keine Option sein (z. B. aus Zeitmangel).

Wir können dieses Problem lösen, indem wir Indizes von Elementen des Originaldataset speichern, das jedes Bootstrap-Sample gebildet hat. Dies ist, was boot.arrayFunktion (mit indices=T Argument) tut.

tableOfIndices<-boot.array(myBootstrap, indices=T)

Jede Zeile ist ein Bootstrap-Beispiel. Z., unsere erste probe enthält thefollowing elemente:

Einstellung indices=F (ein standard), wir’ll erhalten eine antwort auf die frage „Wieviele mal jedes element von original datensatz erschien in jeder bootstrapsample?“. Zum Beispiel in der ersten Probe: das 1. Element des Datensatzes erschien einmal, das 2. Element erschien überhaupt nicht, das 3. Element erschien einmal, das 4. Zweimal und so weiter.

Eine Tabelle wie diese ermöglicht es uns, die Bootstrap-Realisierung außerhalb von R neu zu erstellen.Oder in R selbst, wenn wir set.seed nicht verwenden und die gesamte Berechnung erneut durchführen möchten.

onceAgain<-apply(tableOfIndices, 1, foo, data=iris, cor.type='s')

Überprüfen wir, ob die Ergebnisse identisch sind:

Ja, das sind sie!

Wenn Sie mehr über maschinelles Lernen in R erfahren möchten, besuchen Sie den Machine Learning Toolbox-Kurs von DataCamp.