Das Sonnensystem: Die Erde und der Mond

BY admin
|

Die Planeten sind Dutzende und Hunderte Millionen Kilometer von uns entfernt. Um die Verwendung solch großer Zahlen zu vermeiden, wird die Astronomische Einheit (AU) als Entfernungseinheit verwendet, dh die durchschnittliche Entfernung zwischen der Erde und der Sonne, 149.600.000 km.Licht benötigt 8 Minuten und 19 Sekunden, um diese Strecke zurückzulegen.

Die Größe des Sonnensystems übersteigt die Umlaufbahn von Pluto bei 40 AU und ist definiert als eine, in der die Anziehungskraft der Sonne gleich der Anziehungskraft der Sterne ist, die uns am nächsten sind. Die Abmessungen des Sonnensystems lägen dann in der Größenordnung von 1, 5 105 AU. Offensichtlich sind diese Dimensionen im Vergleich zu den Dimensionen der Galaxie oder des sichtbaren Universums sehr klein. Die Einheiten, die zur Messung dieser enormen Entfernungen verwendet werden, sind das Lichtjahr und der Parsec, der 206 265 AU oder 3, 26 Lichtjahren entspricht.

Die Planeten des Sonnensystems sind in zwei Gruppen unterteilt: die terrestrische Gruppe, die aus Merkur, Venus, Erde und Mars besteht, und die Riesenplanetengruppe, die aus Jupiter, Saturn, Uranus und Neptun besteht.

Alle Planeten außer Venus und Merkur haben Satelliten, von denen die meisten zu den Riesenplaneten gehören. Die Erde, Jupiter, Saturn und Neptun haben die größten Satelliten: den Mond, die von Galileo entdeckten Satelliten des Jupiter (Io, Europa, Ganymed, Callisto), den Satelliten Titan des Saturn und Triton des Neptun.

Asteroiden besetzen eine riesige ringförmige Region zwischen den Umlaufbahnen von Mars und Jupiter in einer durchschnittlichen Entfernung von 2,75 AE von der Sonne. Der größte Asteroid ist Ceres mit einem Durchmesser von 1000 km.

Kometen, die etwa 600 katalogisiert wurden, sind in zwei Gruppen unterteilt, kurze Periode (unter 20 Jahren) und lange Periode (über 20 Jahre). Es gibt mehrere Hypothesen über den Ursprung von Kometen, darunter die des niederländischen Astronomen J. Oort.

Zusätzlich zu den im interplanetaren Raum erwähnten Körpern gibt es eine große Anzahl von Partikeln unterschiedlicher Größe, vorwiegend solche mit einer Masse von Tausendstel oder Millionstel Gramm, die als Meteorstaub bezeichnet werden. Die Bildung dieser Teilchen ist wahrscheinlich auf die Kollision größerer Körper (Asteroiden) und ihre sukzessive Fragmentierung während der Existenz und Entwicklung des Sonnensystems zurückzuführen.

Meteorstaub ist für das Phänomen des Tierkreislichts verantwortlich, das nach Einbruch der Dunkelheit oder vor Sonnenaufgang aufgrund der Lichtstreuung durch diese Staubpartikel beobachtet wird. Die meisten Partikel verdampfen beim Eintritt in die Erdatmosphäre (in Höhen zwischen 80 und 120 km), nur ein kleiner Teil erreicht die Erdoberfläche.

Schauen wir uns nun einige Daten zu den Planeten des Sonnensystems an

Zuerst der Sonne

himmelskörper Radio Masse
Sonne 6,96·108 m 1,98·1030 Kilogramm

Dann, aus dem Land

himmelskörper Halbachse Periode Masse
Erde 149,6·109 m 1 Jahr=365,26 Tage 5.98*1024 Kilogramm

und der Rest der Planeten

Planet Halbachse (AU) Exzentrizität Periode (Jahre) Masse
Quecksilber 0.387 0.206 0.24 0.06
Venus 0.723 0.007 0.62 0.82
Erde 1.000 0.017 1.00 1.00
Mars 1.524 0.093 1.88 0.11
Jupiter 5.203 0.048 11.86 318
Saturn 9.539 0.056 29.46 95.1
Uranus 19.182 0.047 84.01 14.6
Neptun 30.058 0.009 164.8 17.2

In der folgenden Tabelle sind als ergänzende Daten zur Verfügung gestellt:

  • Die Neigung der Ebene der Umlaufbahn des Planeten in Bezug auf die Ekliptik (Ebene der Umlaufbahn der Erde)
  • Die Periode der Rotation um seine Achse. Es war sehr schwierig, diese Größe für Planeten wie Merkur und Venus zu messen. Die gasförmigen Schalen von Jupiter, Saturn, Uranus und Neptun besitzen die Eigenschaft einer differentiellen Rotation, dh ihre Rotationsperioden variieren je nach Breitengrad.
  • Die Neigung der Drehachse in Bezug auf die Ebene der Umlaufbahn. Im Fall der Venus sind es 177º, was der Aussage entspricht, dass die Neigung der Achse 3º beträgt, die Drehrichtung jedoch umgekehrt ist. Das gleiche Argument gilt für Uranus, was darauf hinweist, dass die Rotationsachse von Uranus fast in der Ebene seiner Umlaufbahn liegt.
Planet Neigung der Umlaufbahn Rotationsperiode Dichte g / cm3 Radioäquator (km) Achsenneigung Nein. von Satelliten
Merkur 7.0 58d.6 5.44 2 439 < 30º 0
Venus 3. Platz.4 243d 5.24 6 051 177 ° 0
Erde 0 23 stunden.9 5.52 6 378 23.5 1
Mars 1.Platz 8 24 Stunden.6 3.95 3 394 25º.2 2
Jupiter 1.Platz 3 9h.9 1.33 71 398 3.1 16
Saturn 2. Platz.5 10 stunden.2 0.69 60 000 26º.4 17
Uranus 0º.8 10 stunden.8 1.26 25 400 98º 5
Neptun 1.8 15 Uhr.8 1.67 24 750 29º 2
Sehen Sie die Planeten nach oben:

Satelliten

Schließlich stellen wir einige Daten zu den wichtigsten Satelliten der Planeten zur Verfügung. Jupiter und Saturn haben viele Satelliten, die viel größer sind als die des Mars, aber wir erwähnen nur diejenigen, die ähnlich groß oder größer als unser Mond sind.

Planet Satelliten Dichte g / cm3 mittlerer Radius (km) Funkbahn (103 km) Zeitraum (Tage)
Erde Mond 3.33 1 738 384.4 27.32
Mars Phobos 2.1 13.5 9.38 0.319
Deimos 2.1 7.5 23.46 1.262
Jupiter Io 3.53 1 820 421.6 1.769
Europa 3.03 1 565 670.9 3.551
Ganymed 1.93 2 638 1 070 7.155
Calisto 1.83 2 410 1 880 16.689
Saturn Titanen 1.9 2 575 1 221.9 15.95
Neptun Molch 2 200 394.7 5.84

Aktivitäten

  1. Bestimmen Sie die Masse des Planeten Jupiter aus den Funkdaten und der Umdrehungsperiode eines seiner Satelliten.

    2. Beispiel: Bestimmen Sie die Masse des Planeten Jupiter mit dem Wissen, dass der Radius der Umlaufbahn von Io 421.600 km beträgt und dass seine Umlaufzeit 1.769 Tage beträgt. Tatsache: Die Konstante G ist 6,67 * 10-11 Nm2 / kg2

  2. Bestimmen Sie den Radius der Umlaufbahn eines Satelliten des Planeten Jupiter aus der Masse dieses Planeten und der Umdrehungsperiode des Satelliten.

    3. Beispiel: Berechnen Sie den Radius der Umlaufbahn des Satelliten Callisto zu wissen, dass seine Umlaufzeit 16.689 Tage beträgt und die Masse des Planeten Jupiter 1.901 · 1027 kg beträgt. Daten: Die Konstante G beträgt 6,67 * 10-11 Nm2/ kg2

  3. Bestimmen Sie die Intensität des Gravitationsfeldes g auf der Oberfläche der Planeten und einiger Satelliten aus den Daten ihrer Masse M und ihres Radius R oder ihrer Dichte ρ und ihres Radius.

    4. g=G M R 2 = 4π 3 GpR

    Daten: Die Konstante G ist 6.67 * 10-11 Nm2 / kg2

Der Mond

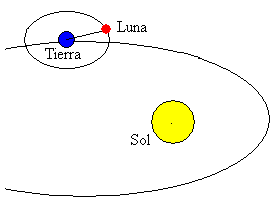
Der Mond ist einer der größten Körper im Sonnensystem. Seine Umlaufbahn ist fast kreisförmig (Exzentrizität ε = 0, 05) und die Ebene seiner Umlaufbahn ist um 5º gegenüber der Ebene der Erdumlaufbahn geneigt.

Die durchschnittliche Entfernung zwischen dem Erdmittelpunkt und dem Mond beträgt 384.400 km.Seine Rotationsperiode um die Erde beträgt 27.322 Tage. Die Änderung der Position des Mondes in Bezug auf die Sonne führt zu den Mondphasen.

Der Mond zeigt dem terrestrischen Beobachter aufgrund der Wirkung der Gezeitenkräfte, die die Erde auf den Mond ausübt, immer das gleiche Gesicht. Dies bedeutet, dass die Rotationsperiode des Mondes um seine Achse mit der Zeit übereinstimmt, die benötigt wird, um eine Umlaufbahn um die Erde zu vervollständigen.

Der Mond ist das Himmelsobjekt, das die Menschheit am meisten fasziniert hat. Die ehemalige Sowjetunion schickte erstmals ein automatisches Schiff, das 1959 auf der Mondoberfläche landete. Am 20.Juli 1969 war Neil Armstrong in Begleitung von Edwin Aldrin der erste Mann, der im Rahmen der Apollo-11-Mission auf der Mondoberfläche lief. Der letzte Besuch amerikanischer Astronauten auf dem Mond fand 1972 statt.

Der Ursprung des Mondes scheint ungewiss, es gibt mehrere Theorien:

  • es entstand gleichzeitig die Erde mit dem Material aus einem Nebel

  • ein Himmelskörper ist in zwei Teile geteilt, wodurch Erde und Mond entstehen

  • Dass sich der Mond anderswo gebildet hat und von der Erde gefangen genommen wurde

  • Dass die Erde mit einem Himmelsobjekt von großer Größe (etwa der Größe des Mars oder größer) kollidierte und dass der Mond mit dem Material gebildet wurde, das aus dieser Kollision ausgestoßen wurde.

Die letztere Theorie scheint im Moment von der wissenschaftlichen Gemeinschaft am meisten akzeptiert zu werden.

Mondpfad

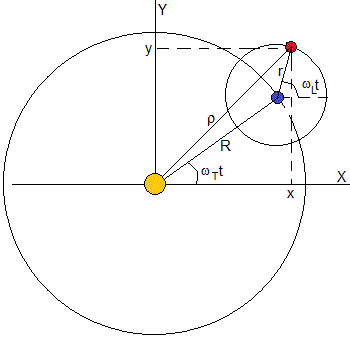
Betrachten Sie einen Planeten und seinen Satelliten. Der Planet beschreibt eine kreisförmige Umlaufbahn des Radius R um seinen Stern mit konstanter Winkelgeschwindigkeit wT = 2π / PT, wobei PT die Periode oder Zeit ist, die zu einer vollständigen Drehung führt. Der Satellit beschreibt eine kreisförmige Umlaufbahn coplanaria des Radius r mit konstanter Winkelgeschwindigkeit wL=2π / PL, wobei PL die Zeit oder die Zeit, die benötigt wird, um eine vollständige Umdrehung zu machen

die Position des Satelliten in Bezug auf ein Bezugssystem, dessen Ursprung der Stern ist, ist

x=Rcos( ω T )+rcos(ω L t ) y=Risiko(ω T )+Risiko(ω L t)

Ist α =wT/wL

{ x=Rcos( α ω L t )+rcos( ω L t ) y=Risiko( α ω L t )+risiko( ω L t) { x=Rcos( α 2π P L t )+rcos( 2π P L t ) y=Risiko(α 2π P L t )+risiko(2π P L t )

wir nennen τ=t/PL

x R =cos( α·2πτ )+ r R cos( 2πτ ) und R =sin( α·2πτ )+ r r sin( 2πτ )

Wir repräsentieren die Flugbahn eines Satelliten für α=0,1 und für drei Werte des Verhältnisses r/ R.

  • r/ R<α. Beispiel: r / R=0,05
  • r/R=α. Beispiel: r / R=0,1
  • r/R >α. Beispiel: r / R=0.15
alfa=0.1;r=0.15;fplot(@(t) r*cos(2*pi*t)+cos(2*pi*alfa*t), @(t) r*sin(2*pi*t)+sin(2*pi*alfa*t),)text(0.1,0.1,sprintf('\alpha=%1.2f',alfa))text(0.1,0.2,sprintf('r/R=%1.2f',r))axis equalgrid onxlabel('x/R')ylabel('y/R')title('Trayectoria de un satélite')

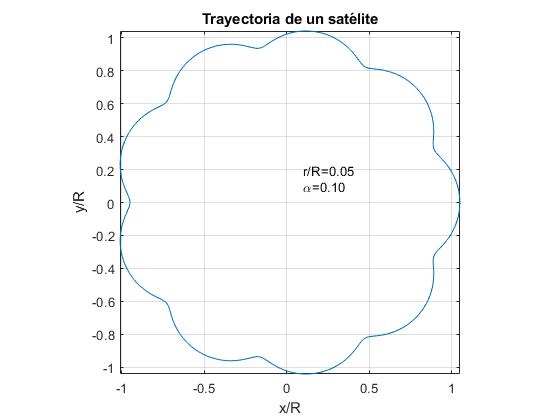
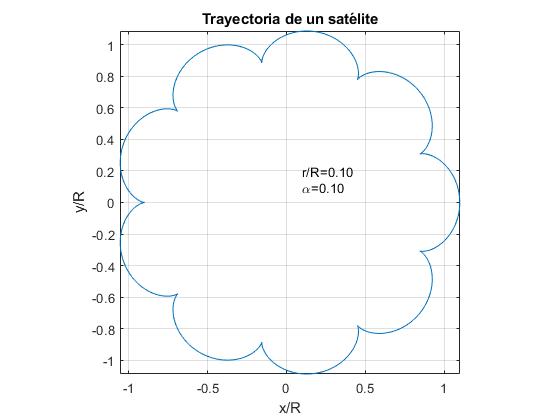
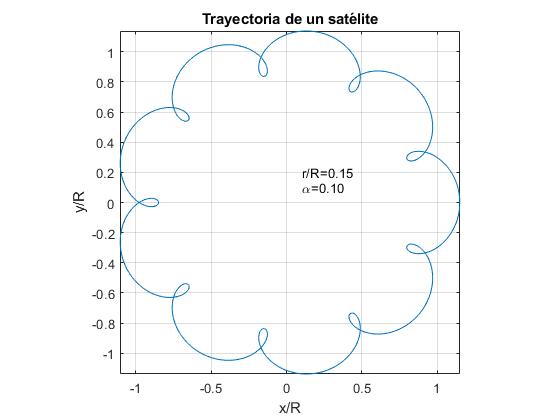
Für den Fall der Erde und des Mondes sind die Daten:

  • radius der Mondumlaufbahn: r = 384,4 · 106 m, Periode PL = 27,32 d
  • Radius der Erdumlaufbahn: R = 149,6 · 109 m, Periode PT = 365,26 d

α = wT / wL = PL / PT = 0,0748. r / R=0,0026

Die Umlaufbahn des Mondes ähnelt der ersten Figur. In der grafischen Darstellung der Flugbahn des Mondes für diese Werte von α und r/R nicht zu schätzen wissen, die Schwingungen der radialen Entfernung zwischen der Sonne und dem Mond

Beschleunigung des Mondes

Der Abstand ρ von der Sonne zum Mond, ist

ρ 2 = x 2 + y 2 = R 2 + r 2 +2rRcos( ( ω L − ω T )t )

wir berechnen die rechteckigen Komponenten der Beschleunigung

{ dx dt =− ω T Risiko( ω T )− ω L risiko( ω L t) dy dt = ω T Rcos( ω T)+ ω L rcos( ω L t) { a x = d 2 x d t 2 =− ω T 2 Rcos( ω T )− ω L 2 rcos( ω L t ) y = d 2 y d t 2 =− ω T 2 Risiko( ω T )− ω L 2 risiko( ω L t )

die radiale Komponente der Beschleunigung

zu ρ = a → · ρ → ρ = a x x+ a y x 2 + y 2 =− ω T 2 R 2 + ω L 2 r 2 +( ω T 2 + ω L 2 )Rrcos( ( ω L − ω T )t ) R 2 + r 2 +2 rr cos( (ω L − ω T )t )

Die Minimal- und Maximalwerte werden erhalten, wenn cos((wL-wT)t)=±1

a maximal = – ω T 2 R 2 + ω L 2 r 2 + ( ω T 2 + ω L 2) Rr R 2 + r 2 +2 rr = -( ω T 2 R + ω L 2 r) minimal = – ω T 2 R 2 + ω L 2 r 2 −( ω T 2 + ω L 2) Rr R 2 + r 2 -2 rr = – ( ω T 2 R- ω L 2 r ) 

>> R=149.6e9; %Tierra>> r=384.4e3; %Luna>> wT=2*pi/(365*24*60*60) %velocidad angular TierrawT = 1.9924e-07>> wL=2*pi/(27.32*24*60*60) %velocidad angular TierrawL = 2.6619e-06>> aM=-(wT^2*R+wL^2*r)aM = -0.0059>> am=-(wT^2*R-wL^2*r)am = -0.0059

Der Mond ist der einzige Satellit im Sonnensystem, dessen radiale Komponente der Beschleunigung negativ ist, es wird gesagt, dass ‚der Mond zur Sonne fällt‘,

Mondphasen

Die Abbildung zeigt den Mond in verschiedenen Positionen in seiner Umlaufbahn um die Erde. Die Sonne ist weit weg und beleuchtet beide Himmelskörper (oben in der Abbildung)

Die Hälfte des Mondes wird von der Sonne beleuchtet (in weißer Farbe) und die Hälfte des der Erde am nächsten gelegenen Mondes ist für den Erdbeobachter sichtbar. Während sich der Mond um die Erde bewegt, sehen wir verschiedene Bruchteile des von der Sonne beleuchteten Teils (die gelben Bereiche).

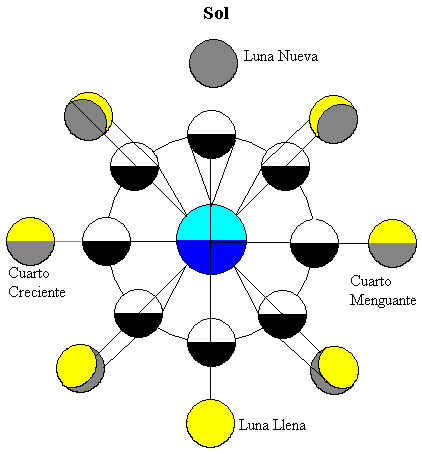
  • Wenn der Mond zwischen der Erde und der Sonne ist, ist der Teil des Mondes, der der Erde am nächsten liegt, dunkel, so dass wir den Mond nicht sehen können.

  • Wenn sich die Erde zwischen Sonne und Mond befindet, ist der Teil des Mondes, der der Erde am nächsten liegt, die beleuchtete Hälfte.

  • Wenn sich der Mond in Zwischenpositionen befindet, wird nur die Hälfte des nächsten Teils der Erde beleuchtet. Daher sehen wir nur ein Viertel des Mondes, diese beiden Phasen werden Viertel genannt, die zunehmen oder abnehmen, je nachdem, ob der beleuchtete Teil, der von der Erde aus sichtbar ist, dazu neigt, zu wachsen oder abzunehmen.

Hinweis: Dieses interaktive Programm versucht, die Phasen des Mondes zu erklären, aber es ist eine getreue Darstellung der Umlaufbahn des Mondes, die einen Winkel von 5 ° mit der Ebene der Ekliptik (der Erdumlaufbahn um die Sonne) bilden, oder die Ausrichtung der Achse der Erde, die etwa 23º mit der Normalen zur Ebene der Ekliptik ist.

Eine rote Linie wurde über den Mond gezogen, so dass der Leser das Zusammentreffen der Rotationsperiode des Mondes um seine Achse und die Zeit, die benötigt wird, um eine Umlaufbahn um die Erde zu vervollständigen, schätzen kann und daher der Mond hat immer das gleiche Gesicht zur Erde.

Mondfinsternisse

Mondfinsternisse treten immer dann auf, wenn sich der Mond in voller Phase befindet und wenn Sonne, Erde und Mond in einer geraden Linie liegen. Dann befindet sich der Mond im Schatten der Erde, wie in der Abbildung gezeigt.

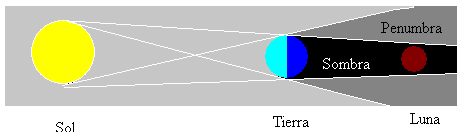
Es gibt andere Arten von Mondfinsternis, die von der Ausrichtung der drei Himmelskörper abhängen. Der Mond kann in einem unbeleuchteten Bereich (Schatten) oder teilweise beleuchtet (Penumbra) sein.

Die Sonnenfinsternis tritt auf, wenn der Mond zwischen der Sonne und der Erde steht, der Mond ist in einer neuen Phase. Der Mond ist 400 mal kleiner als die Sonne, aber der Mond ist 400 mal näher an der Erde, so dass die scheinbare Größe beider Körper von der Erde aus gesehen fast gleich ist. Der Mond kann somit eine totale Sonnenfinsternis erzeugen, wenn er in der vom Mond auf die Erde projizierten Schattenzone beobachtet wird.

Monddaten

Masse (Kilogramm) 7.349·1022
Radius (km) 1737. 4
Durchschnittliche Dichte (g/cm3) 3.34
durchschnittliche Entfernung zur Erde (km) 384 000
Umlaufzeit (Tage) 27.32166
Erdbeschleunigung am Äquator (m/s2) 1.62
Exzentrizität der Umlaufbahn 0.0549
Neigung der Umlaufbahn (Grad) 5.1454

  1. Berechnen Sie den Radius der kreisförmigen Umlaufbahn des Mondes um die Erde, wobei Sie wissen, dass der Zeitraum 27, 32 Tage beträgt. Berechnen Sie auch die Geschwindigkeit des Mondes. Daten: G = 6,67 * 10-11 Nm2 / kg2, die Masse der Erde beträgt M= 5,98 * 1024 kg.

  2. Berechnen Sie die Erdbeschleunigung g auf der Mondoberfläche.

  3. Berechnen Sie den Quotienten zwischen dem Durchmesser der Sonne und dem Durchmesser des Mondes. Berechnen Sie das Verhältnis zwischen der durchschnittlichen Entfernung zwischen Sonne und Erde und dem Mond und der Erde. Daten: Sonnenradius 6,96·108 m, Mittelerde-Sonne Abstand 1,49·1011 m

  4. Berechnen Sie die Position des Massenschwerpunkts des Erde-Mond-Systems, gemessen vom Erdmittelpunkt.

  5. Berechnen Sie die Anziehungskraft der Erde auf dem Mond und vergleichen Sie sie mit der Anziehungskraft der Sonne auf dem Mond. Datum: Sonne masse, 1,98*1030 kg

Referenzen

M. Marov. Planeten des Sonnensystems. Verlag Mir.

Erfahren Sie mehr über Planeten in Wie viele Planeten gibt es in unserem Sonnensystem?. ComofuncionaQue.com

Für den Abschnitt ‚Flugbahn des Mondes‘

David C. Johnston. Zykloidenbahnen in der Physik als Überlagerungen von Translations- und Rotationsbewegungen. Uhr. In: J. Phys.87(10), Oktober 2019, S. 808-810

Der Mond wendet sich immer der Sonne zu. Mathe-Seiten.