Ein Kreis ist gleichmäßig in sechs gleiche Dreiecke unterteilt

Hallo Marilynn,

Zuerst werde ich Ihnen meine Annahmen darüber mitteilen, wie Ihr Bild aussieht:

1. Jedes Dreieck hat einen Scheitelpunkt (Ecke) in der Mitte des Kreises
2. Jedes Dreieck hat Ecken am Umfang des Kreises (zwei Seiten jedes Dreiecks sind also ein Radius)
3. Die Dreiecke teilen sich Seiten (es gibt keine Lücken zwischen den Dreiecken)

Das Gesamtbild sieht aus wie eine Blume – jedes Dreieck ist ein Blütenblatt.

Der unbekannte Bereich ist das, was um die Außenseite des Kreises herum zwischen dem Umfang und der Außenseite jedes Dreiecks verbleibt. Dieser unbekannte Bereich ist in sechs kongruente Abschnitte unterteilt (in jeder Hinsicht gleich – wie die Dreiecke in jeder Hinsicht „gleich“ sind – einschließlich Fläche, Seitenlänge und Bogenlänge). Es ist nicht klar, ob Sie meinen, dass die Fläche eines Bogens Pi ist (nicht wirklich geteilter Kuchen, obwohl er gleich ausgesprochen wird), oder ob alle sechs Abschnitte zusammen Pi sind. Im Folgenden werde ich davon ausgehen, dass einer der äußeren Abschnitte eine Fläche von Pi hat, so dass die Fläche aller sechs Abschnitte zusammengenommen 6 mal Pi beträgt. Wir müssen den Radius des Kreises finden, nennen wir ihn r.

Ich werde auch P verwenden, um für Pi (oder ca. 3.14). Nun gibt es viele Informationen, die wir aus den Dreiecken lernen können:

1. Die Winkel in der Mitte sind alle 60 Grad. Dies liegt daran, dass die sechs Winkel in der Mitte alle gleich sind und ein Kreis 360 Grad hat. Also 360 geteilt durch 6.
2. Jedes Dreieck ist gleichschenklig. Dies liegt daran, dass zwei Seiten gleich sind (die Seiten, die einen Radius haben).
3. Jedes Dreieck ist in der Tat gleichseitig. Da es sich um Iscoceles handelt, sind auch die beiden Außenwinkel gleich. Aber es gibt 180 Grad in einem Dreieck, 60 werden bereits im Mittelwinkel verwendet, so dass 180-60 = 120 Grad für die Außenwinkel übrig bleiben. Aber 120 geteilt durch 2 ist 60 Grad, also sind alle drei Winkel gleich, also sind es Isoscles.
4. Jede Seite in jedem Dreieck hat die Länge r. Dies liegt daran, dass wir 6 kongruente (in jeder Hinsicht „gleiche“) gleichseitige Dreiecke haben und dass zwei Seiten jedes Dreiecks ein Radius sind.

Aus der Geometrie der Dreiecke müssen wir etwas Algebra machen. Da wir eine Fläche kennen und einen Radius benötigen, benötigen wir eine Formel (oder Gleichung) für den Radius in Bezug auf die Fläche (beachten Sie im Folgenden das Ziel einer Formel). Die Fläche des Kreises ist P * r2 (r2 bedeutet r im Quadrat und * bedeutet multiplizieren) Die Fläche der verbleibenden Abschnitte außerhalb der Dreiecke, aber innerhalb des Kreises (eine Fläche, die wir bereits für 6 * P halten) kann auch durch Subtraktion der Fläche der Dreiecke von der Fläche des Kreises ermittelt werden. Wir müssen eine Fläche eines der gleichseitigen Dreiecke finden.

Methode 1 zur Berechnung einer Fläche eines Dreiecks
Die Fläche eines Dreiecks ist b* h/2 Hier ist etwas Trigonometrie erforderlich: Zeichnen Sie eine Linie von einem Scheitelpunkt zu einer gegenüberliegenden Seite, die die gegenüberliegende Seite in zwei Hälften teilt und im rechten Winkel steht. Dies teilt das gleichseitige Dreieck in zwei kongruente rechtwinklige Dreiecke, und die neue Seite ist die Höhe, nennen wir es h. Wir müssen h finden.

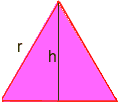
Mit trig in einem der rechtwinkligen Dreiecke haben wir sin60 = h / r, aber sin60 = sqr (3) / 2, wobei sqr (3) die Quadratwurzel von drei bedeutet, also sqr (3) / 2 = h / r multiplizieren Sie beide Seiten mit r, um h zu erhalten = r * sqr (3) / 2 r Jetzt ist die Fläche eines gleichseitigen Dreiecks b * h / 2 = (r) * (r * sqr(3)/2)/2 = ( r2) * sqr (3) / 4 r = sqr (6 * P / (P-6 * sqr (3) / 4)) Verwenden Sie die Reihenfolge der Operationen, um auf einem Taschenrechner zu berechnen (mit P = 3.14): r = 5.896… Der Radius des Kreises beträgt also ca. 5.9. Paulus