Grundlagen der Epidemiologie

BY admin
|

Nachdem Sie dieses Kapitel gelesen haben, können Sie Folgendes tun:

  1. Erklären Sie, was eine Effektmodifikation ist
  2. Unterscheiden Sie zwischen Störfaktoren und Effektmodifikatoren
  3. Führen Sie eine geschichtete Analyse durch, um festzustellen, ob eine Effektmodifikation in den Daten vorhanden ist

Im vorigen Kapitel haben wir Confounding diskutiert. Sie werden sich erinnern, dass ein Confounder eine dritte Variable ist, die, wenn sie nicht angemessen kontrolliert wird, zu einer voreingenommenen Schätzung der Assoziation führt. Effektmodifikation beinhaltet auch eine dritte Variable (nicht die Exposition und nicht das Ergebnis) — aber in diesem Fall wollen wir absolut nicht dafür kontrollieren. Vielmehr ist das Vorhandensein von Effektmodifikationen selbst ein interessanter Befund, den wir hervorheben.

Wenn eine Effektmodifikation (auch Interaktion genannt) vorliegt, gibt es unterschiedliche Ergebnisse für verschiedene Ebenen der dritten Variablen (auch Kovariable genannt). Wenn wir beispielsweise eine Kohortenstudie über die Schlafmenge und den GPA unter Studenten der Oregon State University (OSU) im Laufe eines Semesters durchführen, können wir diese Daten sammeln:

Tabelle 8-1
GPA
< 3.0 ≥ 3.0
Menge an Schlaf < 8 stunden 25 25
> 8 stunden 25 25

Da es sich um eine Kohortenstudie handelte, berechnen wir das Risikoverhältnis (RR):

RR = \frac{\frac{25}{50}}{\frac{25}{50}} = 1.0

Es gibt keinen Zusammenhang zwischen Schlafmenge und nachfolgendem GPA. Unter Verwendung des Vorlagensatzes kann dies angegeben werden:

Schüler, die durchschnittlich weniger als 8 Stunden Schlaf pro Nacht hatten, beendeten das Semester 1,0-mal so häufig mit einem GPA unter 3,0, verglichen mit Schülern, die mindestens 8 Stunden pro Nacht hatten.

Dies ist ein Risikoverhältnis aus einer Kohortenstudie, daher müssen wir den Zeitrahmen einbeziehen — was ich mit den Worten „um den Begriff zu beenden“ getan habe. Genau wie bei der Verwechslung bezeichnen wir dies als unangepasste oder grobe RR.

Wenn wir jedoch mit Studenten sprechen, fragen wir uns, ob das Geschlecht eine wichtige Kovariable sein könnte oder nicht. Wie bei der Verwechslung würden wir eine geschichtete Analyse durchführen, um die Effektmodifikation zu überprüfen. Auch hier zeichnen wir 2 × 2-Tabellen mit der gleichen Exposition (Schlaf) und dem gleichen Ergebnis (GPA), zeichnen jedoch separate Tabellen für Männer und Frauen (Geschlecht ist die Kovariable). Wir tun dies, indem wir uns die Rohdaten ansehen und herausfinden, wie viele der 25 Personen in der obigen A-Zelle (E +, D +) Männer und wie viele Frauen waren. Nehmen wir an, dass von den 25 Personen, die < 8 Stunden berichteten und einen GPA < 3 hatten.0, 11 waren Männer und 14 waren Frauen. Wir teilen dann die Teilnehmer in ähnlicher Weise aus den B-, C- und D-Zellen und erstellen schichtspezifische 2 x 2-Tabellen:

Tabelle 8-2
Männer GPA
< 3.0 ≥ 3.0
Menge an Schlaf < 8 stunden 11 14
8+ stunden 17 9
Tabelle 8-3
Frauen GPA
< 3.0 ≥ 3.0
Menge an Schlaf < 8 stunden 14 11
8+ stunden 8 16
Unter Verwendung von Daten aus den obigen 2 × 2-Tabellen sind die schichtspezifischen RRs wie folgt:

RRmen= \frac{(\frac{11}{25})}{(\ frac{17}{26})} = 0.68

RRwomen= \frac{(\frac{14}{25})}{(\ frac{8}{24})} = 1.7

Interpretationen:

Unter männlichen Studenten hatten diejenigen, die weniger als 8 Stunden pro Nacht schliefen, das 0,68-fache Risiko, einen GPA < 3 zu haben.0 am Ende des Semesters, verglichen mit denen, die 8 oder mehr Stunden gemeldet haben.

Unter den Studentinnen hatten diejenigen, die weniger als 8 Stunden pro Nacht schliefen, das 1,7-fache Risiko, am Ende des Semesters einen GPA < 3,0 zu haben, verglichen mit denen, die 8 oder mehr Stunden berichteten.

Das Schlafen von weniger als 8 Stunden ist — in diesen hypothetischen Daten — mit einem höheren GPA bei männlichen Schülern verbunden (das „Ergebnis“ ist ein niedriger GPA, so dass ein RR von weniger als 1 anzeigt, dass exponierte Personen weniger wahrscheinlich einen niedrigen GPA haben), aber mit einem niedrigeren GPA bei weiblichen Schülern.

Das Geschlecht wirkt in diesem Fall als Effektmodifikator: Die Assoziation zwischen Schlaf und GPA variiert je nach Schichten der Kovariablen. Sie können Effektänderungen erkennen, wenn Sie eine geschichtete Analyse durchführen, wenn Sie Folgendes angeben:

  • Die schichtspezifischen Assoziationsmaße unterscheiden sich voneinander
  • Das Rohöl fällt dazwischen

Wenn Sie eine Änderung vorgenommen haben, müssen Sie im nächsten Schritt die schichtspezifischen Maßnahmen melden. Wir berechnen kein angepasstes Maß (es wäre nahe 1.0, ähnlich dem Rohöl); das Interessante dabei ist, dass Männer und Frauen unterschiedlich auf den Schlaf reagieren. Effektmodifikation ist etwas, das wir in unseren Ergebnissen hervorheben möchten, nicht etwas, das angepasst werden muss.

Anders als beim Confounding, bei dem eine Änderung von 10% von roh zu bereinigt eine akzeptierte Definition für Confounding ist, gibt es keine solche standardisierte Definition dafür, wie unterschiedlich die schichtspezifischen Maßnahmen sein müssen, um etwas als Effektmodifikator zu bezeichnen. Der Schwellenwert sollte wahrscheinlich höher sein als der, der erforderlich ist, um etwas als Störfaktor zu deklarieren, denn sobald Sie etwas als Effektmodifikator deklarieren, sind Sie anschließend verpflichtet, die Ergebnisse für jede Stufe der Kovariablen separat zu melden — etwas, das Ihre Leistung mindestens halbiert. Daher sehen wir in der Epidemiologie selten Hinweise auf Effektmodifikationen, die in der Literatur berichtet werden. Lange Rede kurzer Sinn, „anders“ genug für Effektmodifikation ist „eindeutig anders.“

Beim Lesen von Artikeln wird die Effektmodifikation manchmal als Interaktion bezeichnet, oder die Autoren sagen einfach, dass sie über geschichtete Analysen berichten. Jede dieser 3 Phrasen ist ein Hinweis darauf, dass es eine Variable gibt, die als Effektmodifikator fungiert.

Effektmodifikation Beispiel II

Nach der durch die Immobilienblase verursachten Rezession von 2008 (dies ist die Exposition) hat die US-Wirtschaft viele Arbeitsplätze verloren. Hier ist eine Grafik, die die Anzahl der Menschen zeigt, die vor, während und nach der Rezession gearbeitet haben (das Ergebnis). Die Ergebnisse werden nach Geschlecht geschichtet dargestellt (eine Kovariable), was bedeutet, dass der Analyst vermutete, dass das Geschlecht als Effektmodifikator wirken könnte. In der Tat sind die Ergebnisse etwas anders: Männer (in blau) verloren einen größeren Anteil an Arbeitsplätzen und hatten sich ab 2014 noch nicht auf das Niveau vor der Rezession erholt, während Frauen (in rot) weniger Arbeitsplätze verloren und sich bis 2014 vollständig erholt hatten.

Abbildung 8-1
Quelle: https://fred.stlouisfed.org/graph/fredgraph.png?g=qUs

Was ist, wenn wir auch nach Alter schichten? Zuerst, Hier ist eine Grafik, die zeigt, wie sich die Rezession auf Arbeitsplätze für Menschen im Alter auswirkt 55 und älter:

Abbildung 8-2
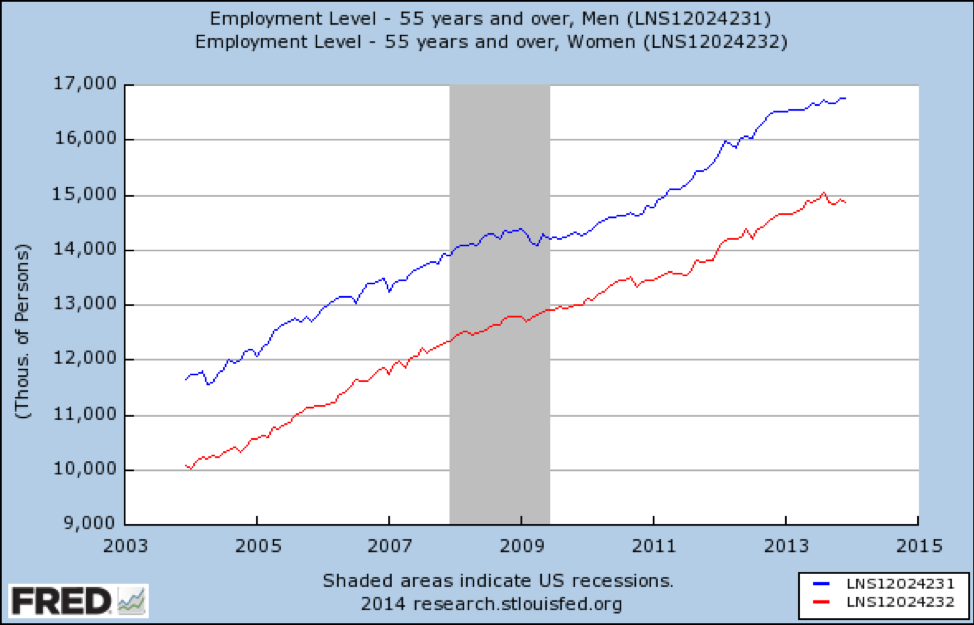
Quelle: https://fred.stlouisfed.org/graph/fredgraph.png?g=qUt

Die Rezession betraf ältere arbeitende Amerikaner überhaupt nicht. Wir sehen auch keine Effektmodifikation nach Geschlecht – die 2 Linien sind fast parallel.

Was ist mit jungen Erwachsenen?

Abbildung 8-3
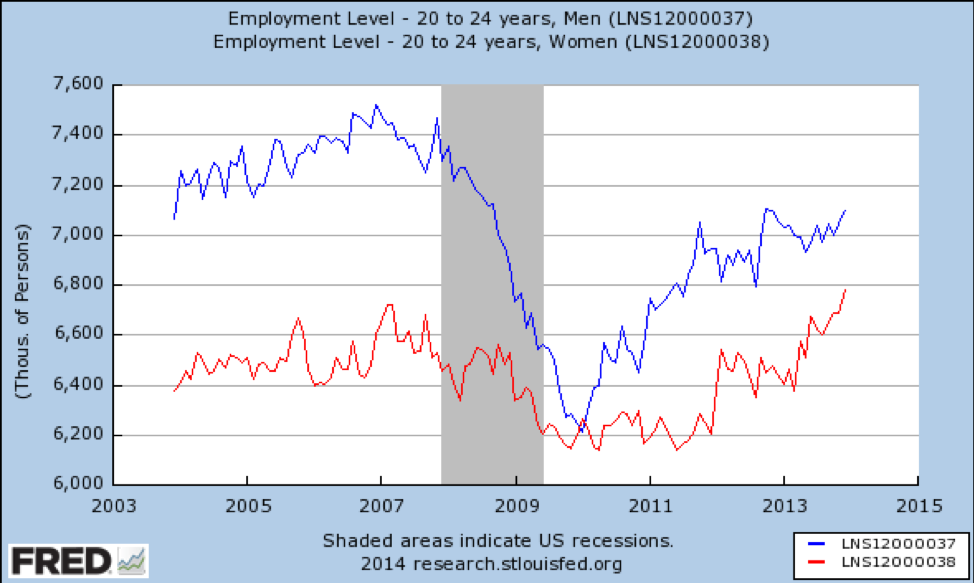
Quelle: https://fred.stlouisfed.org/graph/fredgraph.png?g=qUv

Hier haben wir große Auswirkungen Veränderung nach Geschlecht-junge Männer verloren einen großen Teil der verfügbaren Arbeitsplätze und hatte nicht vollständig ab 2014 erholt. Dies ist nicht verwunderlich, da die Rezession hauptsächlich durch die Immobilienblase verursacht wurde und die Bauarbeiter hauptsächlich junge Männer sind. Im Gegensatz dazu verloren junge Frauen einen kleinen Teil der Arbeitsplätze und erholten sich schnell auf ein Niveau, das besser war als vor der Rezession.

Schließlich betrachten wir Jobs für 25- bis 54-Jährige:

Abbildung 8-4
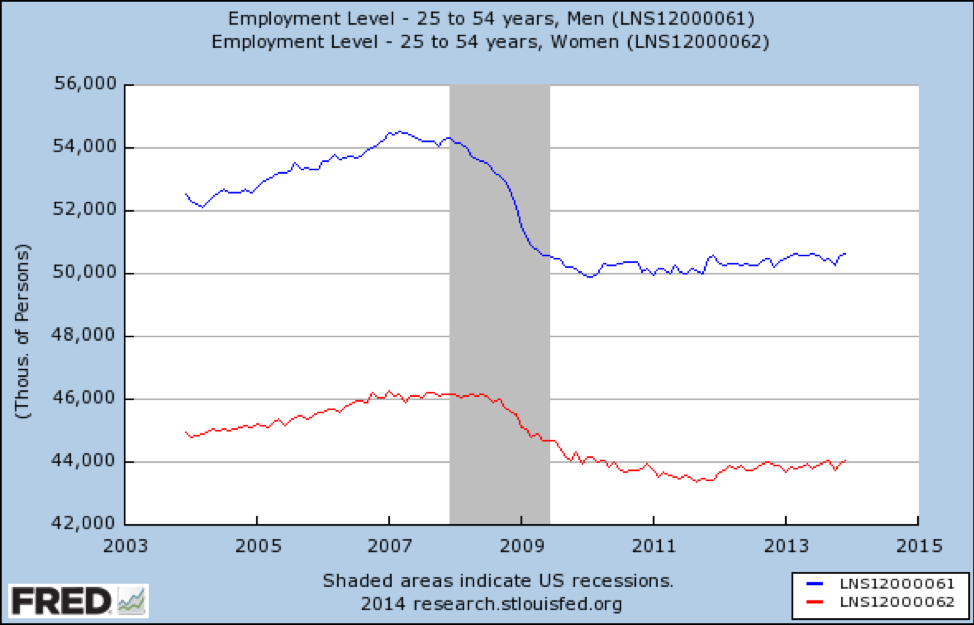
Quelle: https://fred.stlouisfed.org/graph/?id=LNS12000061

Hier sehen wir ein sehr düsteres Bild. In dieser Altersgruppe gingen Arbeitsplätze verloren – mehr für Männer als für Frauen — und hatten sich 2014 überhaupt nicht erholt.

Wenn wir also die Reaktion des Arbeitsmarktes auf die Rezession von 2008 untersuchen, sehen wir eine erhebliche Veränderung der Auswirkungen nach Alter (die Erholung der Arbeitsplätze schwankte drastisch nach Alter) und innerhalb einiger Alterskategorien auch einige Hinweise auf eine Veränderung der Auswirkungen nach Geschlecht. Die Auswirkungen der Rezession auf die Arbeitsplätze waren für Menschen unterschiedlichen Alters und Geschlechts unterschiedlich.

Dies ist wichtig, weil die politischen Implikationen sehr unterschiedlich wären. Stellen Sie sich vor, Sie arbeiten als Teil der Bundesregierung und versuchen, ein Konjunkturpaket zu entwerfen. Wenn die einzigen Daten, die Sie hatten, aus dem ersten Diagramm stammten, ohne die Altersaufschlüsselungen, Die potenziellen politischen Lösungen wären sehr unterschiedlich, als wenn Sie auch Zugriff auf die Stratified-by-Age-Analyse hätten.

Beim Confounding erhalten Sie zunächst die falsche Antwort, da der Confounder nicht gleichmäßig auf Ihre Gruppen verteilt ist. Dies verzerrt das von Ihnen berechnete Assoziationsmaß (denken Sie daran: Größere Füße sind nur mit der Lesegeschwindigkeit verbunden, da sie nach Klassenstufe verwechselt werden). Stattdessen müssen Sie das Assoziationsmaß neu berechnen und diesmal den Confounder anpassen.

Mit dieser Modifikation erhalten Sie auch zunächst die falsche Antwort, aber diesmal liegt es daran, dass Ihre Stichprobe mindestens 2 Untergruppen enthält, in denen die Exposition / Krankheitsassoziation unterschiedlich ist. In diesem Fall müssen Sie diese Untergruppen dauerhaft trennen und Ergebnisse (die möglicherweise durch andere Kovariablen verwechselt werden) für jede Schicht separat melden: in diesem Fall haben Männer, die weniger schlafen, höhere GPAs als Männer, die mehr schlafen, aber gleichzeitig haben Frauen, die mehr schlafen, höhere GPAs als Frauen, die weniger schlafen.

Hier ist eine Übersichtstabelle, die den Prozess zum Umgang mit potenziellen Störfaktoren und Effektmodifikatoren angibt. Ein Großteil des Prozesses ist derselbe, unabhängig davon, welche Art von Kovariable Sie haben (in allen Fällen müssen Sie die Kovariable während Ihrer Studie messen und gut messen!). Differenzbereiche sind rot dargestellt.

Tabelle 8-4
Confounding Effektmodifikation
Bevor Sie eine Studie planen Überlegen Sie, welche Variablen als Störfaktoren wirken könnten, basierend auf dem, was Sie über den untersuchten Expositions- / Krankheitsprozess wissen. Überlegen Sie, welche Variablen als Effektmodifikatoren wirken könnten, basierend auf dem, was Sie über den untersuchten Expositions- / Krankheitsprozess wissen.
Während einer Studie Daten über mögliche Kovariablen sammeln – stratifizierte / bereinigte Analysen können nicht ohne Daten zur Kovariablen durchgeführt werden! Sammeln Sie Daten über mögliche Kovariablen – stratifizierte / bereinigte Analysen können nicht ohne Daten zur Kovariablen durchgeführt werden!
Analyse: Schritt 1 Berechnen Sie das grobe Assoziationsmaß (Ignorieren der Kovariablen). Berechne das grobe Assoziationsmaß (ignoriere die Kovariable).
Analyse: Schritt 2 Berechnen Sie schichtspezifische Assoziationsmaße, sodass jede Ebene der Kovariablen eine eigene 2 x 2-Tabelle hat. Berechnen Sie schichtspezifische Assoziationsmaße, sodass jede Ebene der Kovariablen eine eigene 2 x 2-Tabelle hat.
Analyse: Schritt 3 Wenn die schichtspezifischen Maße einander ähnlich sind und sich mindestens 10% vom Rohmaterial unterscheiden (das nicht zwischen sie fällt), dann ist die Kovariable ein Störfaktor. Wenn sich die schichtspezifischen Maße voneinander unterscheiden und der Unterschied zwischen ihnen liegt, ist die Kovariable ein Effektmodifikator.
Writing Results Gibt ein angepasstes Assoziationsmaß an, das für den Confounder steuert. Berichten Sie über die schichtspezifischen Assoziationsmaßnahmen.

Stellen Sie sich vor, Sie machen eine Querschnittsstudie über körperliche Aktivität und Demenz bei älteren Menschen und berechnen eine unangepasste Odds Ratio (OR) von 2,0. Sie denken, dass der Familienstand eine wichtige Kovariable sein könnte, also schichten Sie nach „derzeit verheiratet“ versus „derzeit nicht verheiratet“ (was nie verheiratet, geschieden und verwitwet beinhaltet). Der ODER unter den derzeit verheirateten Personen beträgt 3,1, und unter den derzeit nicht verheirateten Personen beträgt der ODER 3,24. In diesem Fall fungiert der Familienstand als Störfaktor, und wir würden das angepasste ODER melden (was ungefähr 3,18 wäre).

Stellen Sie sich vor, Sie führen eine randomisierte Studie einer Mittelmeerdiät durch, um eine Frühgeburt bei schwangeren Frauen zu verhindern. Sie machen den Versuch und berechnen eine RR von 0,90. Sie denken, dass vielleicht Parität eine wichtige Kovariable sein könnte, also führen Sie eine geschichtete Analyse durch. Unter Nulliparas ist die RR 0,60 und unter Multiparas ist die RR 1,15. Diese unterscheiden sich voneinander, und der Unterschied liegt zwischen ihnen. In diesem Fall fungiert die Parität als Effektmodifikator, sodass Sie die 2 schichtspezifischen RRs separat melden würden.

Stellen Sie sich vor, Sie machen eine Fall-Kontroll-Studie zum Melanom und zur vorherigen Verwendung des Solariums. Das rohe OR ist 3,5, aber vielleicht ist das Geschlecht eine wichtige Kovariable. Die geschichtete Analyse ergibt einen OR von 3,45 bei Männern und 3,56 bei Frauen. In diesem Fall ist die Kovariable (Geschlecht) weder ein Störfaktor noch ein Effektmodifikator. Wir sagen, dass es kein Störfaktor ist, weil (1) das Rohöl zwischen den 2 schichtspezifischen Schätzungen liegt, aber auch (2) die schichtspezifischen Schätzungen sich nicht mehr als 10% vom Rohöl unterscheiden. Wir sagen, dass es kein Effektmodifikator ist, weil 3,45 und 3,56 nicht so unterschiedlich sind — in beiden Fällen gibt es einen erheblichen Effekt (ungefähr 3,5 mal so hoch). Wir würden die grobe Schätzung der Assoziation melden, da weder eine Anpassung noch eine Schichtung erforderlich ist, um die Auswirkungen des Geschlechts zu berücksichtigen.

Ja! Normalerweise sehen wir dies, wenn die fragliche Kovariable eine kontinuierliche Variable ist, die zwecks Überprüfung auf Effektmodifikation dichotomisiert wird. Zum Beispiel, wenn wir denken, dass das Alter ein Effektmodifikator sein könnte, Wir könnten unsere Stichprobe für die geschichtete Analyse in „alt“ und „jung“ unterteilen — sagen, älter als 50 gegen 50 oder jünger. In dem Maße, in dem 51-Jährige nicht wie 70-Jährige sind, könnten wir einige wichtige Nuancen in den Ergebnissen vermissen, möglicherweise weil es in den Daten eine weitere Effektmodifikation mit mehr Kategorien gibt (was die Potenz auf fast nichts reduzieren würde, wenn wir separat über zusätzliche Schichten berichten würden) oder „residuale“ Verwirrungen, wie im vorherigen Kapitel diskutiert. Weitere Details gehen über den Rahmen dieses Buches hinaus, aber wissen Sie, dass dieselbe Kovariable theoretisch sowohl als Störfaktor als auch als Effektmodifikator fungieren kann — aber dass man dies in der Praxis selten sieht.

Fazit

Im Gegensatz zur Verwechslung, deren Auswirkungen wir in unserer Analyse beseitigen möchten, ist die Effektmodifikation an und für sich ein interessanter Befund, über den wir berichten. Führen Sie eine geschichtete Analyse durch, um die Effektmodifikation zu überprüfen. Wenn die schichtspezifischen Assoziationsmaße unterschiedlich sind und der Unterschied zwischen ihnen liegt, ist es wahrscheinlich, dass die betreffende Variable als Effektmodifikator fungiert. Berichten Sie die Ergebnisse separat für jede Schicht der Kovariablen.

Eine letzte, alles-in-allem-Tabelle:

Tabelle 8-5
Wenn dies Ihre ORs / RRs sind:
Roh / Unangepasst Stratum Stratum Dann ist die Kovariable … Und Sie würden berichten…
2.0 1.0 3.2 ein Effektmodifikator die 2 schichtspezifischen Assoziationsmaße
2.0 3.5 3.6 ein Confounder ein angepasstes Maß
2.0 1.9 2.0 nichts Interessantes das grobe Maß

Ein systematischer Fehler in einer Studie (manche Leute nennen es einen Bias; ich ziehe es vor, nicht), der durch eine dritte Variable verursacht wird, die in die Beziehung zwischen Exposition und Krankheit eingreift.

Bezieht sich auf das Szenario, in dem die Beziehung zwischen einer Exposition und einem Ergebnis auf der Grundlage einer dritten Variablen variiert. Zum Beispiel verhindert Yoga vielleicht ACL-Verletzungen bei Frauen, aber nicht bei Männern. Sex in diesem Szenario ist der Effektmodifikator. Effektmodifikation ist nicht dasselbe wie Verwirren.

Die Wahrscheinlichkeit, dass Ihre Studie etwas findet, das da ist. Leistung = 1 – β; beta ist die Typ-II-Fehlerrate. Kleine Studien oder Studien zu seltenen Ereignissen sind in der Regel unterversorgt.

Wie viele Kinder eine Frau hatte. Nullipare Frauen (auch bekannt als Nulliparas) hatten noch kein erstes Kind (sie sind möglicherweise schwanger, haben das Kind aber noch nicht bekommen), und paröse Frauen hatten mindestens ein vorheriges Kind. Multiparas hatten mindestens zwei frühere Kinder; Primiparas hatten ein vorheriges Kind.

Dies ist die erste Schwangerschaft einer Frau.

Diese Frau hatte andere Kinder.