Hidden Markov Modell: Einfache Definition & Überblick

Statistikdefinitionen >

Das Hidden-Markov-Modell (HMM) ist eine relativ einfache Methode zur Modellierung sequentieller Daten. Ein verstecktes Markov-Modell impliziert, dass das den Daten zugrunde liegende Markov-Modell für Sie verborgen oder unbekannt ist. Genauer gesagt kennen Sie nur Beobachtungsdaten und keine Informationen über die Zustände. Mit anderen Worten, es gibt einen bestimmten Modelltyp, der die Daten erzeugt (ein Markov-Modell), aber Sie wissen nicht, welche Prozesse sie erzeugen. Grundsätzlich verwenden Sie Ihr Wissen über Markov-Modelle, um eine fundierte Vermutung über die Struktur des Modells anzustellen.

Was ist ein Markov-Modell?

Um das versteckte Markov-Modell aufzudecken, müssen Sie zunächst verstehen, was ein Markov-Modell überhaupt ist. Hier werde ich ein einfaches Beispiel mit zwei Elementen erstellen, die in der Wahrscheinlichkeit sehr vertraut sind: Würfel und Säcke mit farbigen Kugeln.

Die Modellkomponenten, die Sie zum Erstellen des Zufallsmodells verwenden, sind:

• Ein sechsseitiger roter Würfel.
• Ein zehnseitiger schwarzer Würfel.
• Ein roter Beutel mit zehn Kugeln. Neun Kugeln sind rot, einer ist schwarz.
• Eine schwarze Tasche mit zwanzig Kugeln. Ein Ball ist rot, neunzehn sind schwarz.

“ Schwarz“ und „Rot“ sind die beiden Zustände in diesem Modell (mit anderen Worten, Sie können schwarz oder rot sein).
Erstellen Sie nun das Modell, indem Sie die folgenden Schritte ausführen:

1. ERSTER SCHRITT: Würfeln Sie einen Würfel. Notieren Sie sich die Nummer, die auftaucht. Das ist die Emission. In der obigen Grafik habe ich einen roten Würfel zum Starten gewählt (willkürlich — ich hätte schwarz wählen können) und 2 gewürfelt.
2. ÜBERGANGSSCHRITT: Wähle zufällig einen Ball aus dem Beutel mit der Farbe, die zu dem Würfel passt, den du in Schritt 1 gerollt hast. Ich habe einen roten Würfel geworfen, also wähle ich einen Ball aus der roten Tasche. Ich zog einen schwarzen Ball heraus, also werde ich für die nächste Emission zum schwarzen Würfel wechseln.

Sie können diese Schritte dann bis zu einer bestimmten Anzahl von Emissionen wiederholen. Wenn Sie diese Schrittfolge beispielsweise 10 Mal wiederholen, erhalten Sie möglicherweise die Menge {2,3,6,1,1,4,5,3,4,1}. Der Prozess des Übergangs von einem Zustand in den nächsten wird als Markov-Prozess bezeichnet.

Der Übergang von Rot zu Schwarz oder Schwarz zu Rot birgt unterschiedliche Wahrscheinlichkeiten, da sich in den Beuteln eine unterschiedliche Anzahl schwarzer und roter Kugeln befindet. Das folgende Diagramm zeigt die Wahrscheinlichkeiten für dieses spezielle Modell mit zwei Zuständen (schwarz und rot):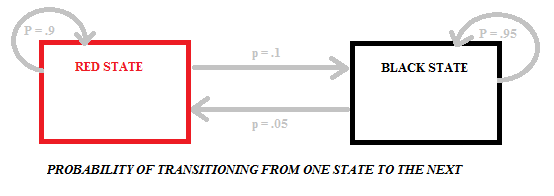

Hidden Markov Model Notation

λ = (A,B,π) ist eine Kurzschreibweise für ein HMM. Andere Notation wird in Hidden Markov-Modellen verwendet:

• A = Zustandsübergangswahrscheinlichkeiten (aij)
• B = Beobachtungswahrscheinlichkeitsmatrix (bj(k))
• N = Anzahl der Zustände im Modell {1,2…N} oder der Zustand zum Zeitpunkt t →st
• M = Anzahl der eindeutigen Beobachtungssymbole pro Zustand
• Q = {q0, q1, . . . , qN-1} = verschiedene Zustände des Markov-Prozesses
• T = Länge der Beobachtungssequenz
• V = {0, 1, . . . , M − 1} = Menge möglicher Beobachtungen
• O = (O0, O1, . . . , OT -1) = Beobachtungssequenz
• π = Anfangszustandsverteilung (ni)
• s = Zustand oder Zustandssequenz (s1, s2… sn)
• xk = versteckter Zustand
• zk = Beobachtung.

Drei grundlegende Probleme

Drei grundlegende Probleme können mit versteckten Markov-Modellen gelöst werden:

1. Angesichts des Hidden-Markov-Modellsλ = (A, B, π) und eine Folge von Beobachtungen O, finden Sie die Wahrscheinlichkeit einer Beobachtung P(O | λ). Dies wird manchmal als Bewertungsproblem bezeichnet.
2. Finden Sie angesichts des Hidden-Markov-Modellsλ = (A, B, π) und einer Beobachtungssequenz O die wahrscheinlichste Zustandssequenz (s1, s2 … sn). Dies wird manchmal als Decodierungsproblem bezeichnet.
3. Finden Sie eine Beobachtungssequenz (O1, O2…) und das Markov-Modell λ = (A, B, π), das die Wahrscheinlichkeit von O maximiert.

Rabiner, L.R. „Ein Tutorial zu Hidden Markov-Modellen und ausgewählten Anwendungen in der Spracherkennung“, Proceedings of the IEEE, vol.77, S. 257-286, Feb. 1989.
Stempel, M. (2013). Eine aufschlussreiche Einführung in Hidden Markov Modelle. Abgerufen 8/6/2013 von: http://www.cs.sjsu.edu/~stamp/RUA/HMM.pdf

——————————————————————————

Benötigen Sie Hilfe bei einer Hausaufgabe oder Testfrage? Mit Chegg Study erhalten Sie Schritt-für-Schritt-Lösungen für Ihre Fragen von einem Experten auf diesem Gebiet. Deine ersten 30 Minuten mit einem Chegg Tutor sind kostenlos!