Logarithmen in der realen Welt verwenden

Logarithmen sind überall. Verwenden Sie jemals die folgenden Sätze?

• 6 zahlen
• Zweistellig
• Größenordnung
• Zinssatz

Sie beschreiben Zahlen in Bezug auf ihre Potenzen von 10, einem Logarithmus. Und ein Zinssatz ist der Logarithmus des Wachstums einer Investition.

Überrascht, dass Logarithmen so häufig vorkommen? Ich auch. Die meisten mathematischen Versuche in der realen Welt (TM) weisen auf Logarithmen in einer arkanen Formel hin oder tun so, als wären wir Geologen, die von der Richterskala fasziniert sind. „Wissenschaftler kümmern sich um Protokolle, und Sie sollten auch. Können Sie sich eine Welt ohne Zink vorstellen?“

Nein, nein, nein, nein nein, nein nein! Mama mia!)

Math drückt Konzepte mit Notation wie „ln“ oder „log“ aus. „Mathematik in der realen Welt“ zu finden bedeutet, Ideen im Leben zu begegnen und zu sehen, wie sie mit Notation geschrieben werden können. Suchen Sie nicht nach den wörtlichen Symbolen! Wann haben Sie das letzte Mal ein Divisionszeichen geschrieben? Wann hast du das letzte Mal etwas zu essen gehackt?

Ok, ok, wir verstehen es: Worum geht es bei Logarithmen?

Logarithmen finden die Ursache für einen Effekt, dh die Eingabe für eine Ausgabe

Ein häufiger „Effekt“ besteht darin, dass etwas wächst, z. B. In 5 Jahren von \ $ 100 auf \ $ 150. Wie kam es dazu? Wir sind uns nicht sicher, aber der Logarithmus findet eine mögliche Ursache: Eine kontinuierliche Rückkehr von ln (150/100) / 5 = 8,1% würde diese Änderung erklären. Es könnte nicht die eigentliche Ursache sein (hat das ganze Wachstum im letzten Jahr stattgefunden?), aber es ist ein glatter Durchschnitt, den wir mit anderen Änderungen vergleichen können.

Übrigens ist der Begriff „Ursache und Wirkung“ nuanciert. Warum ist 1000 größer als 100?

• 100 ist 10, die für 2 Zeiträume von selbst wuchs ($10 * 10$)
• 1000 ist 10, die für 3 Zeiträume von selbst wuchs ($10 * 10 * 10$)

Wir können uns Zahlen als Ausgaben vorstellen (1000 ist „1000 Ausgaben“) und Eingaben („Wie oft muss 10 wachsen, um diese Ausgaben zu erzielen?“). Also,

1000 outputs > 100 outputs

weil

3 inputs > 2 inputs

Oder mit anderen Worten:

log(1000) > log(100)

Warum ist das nützlich?

Logarithmen stellen Zahlen auf eine menschenfreundliche Skala.

Große Zahlen brechen unser Gehirn. Millionen und Billionen sind „wirklich groß“, obwohl eine Million Sekunden 12 Tage und eine Billion Sekunden 30.000 Jahre sind. Es ist der Unterschied zwischen einem amerikanischen Urlaubsjahr und der Gesamtheit der menschlichen Zivilisation.

Der Trick zur Überwindung der „Riesenzahlenblindheit“ besteht darin, Zahlen in Bezug auf „Eingaben“ (dh ihre Leistungsbasis 10) zu schreiben. Diese kleinere Skala (0 bis 100) ist viel einfacher zu erfassen:

• Leistung von 0 = $10^0$ = 1 ( einzigen artikel)
• power von 1 = $10^1$ = 10
• potenz von 3 = $ 10 ^ 3 $ = Tausend
• Potenz von 6 = $ 10 ^ 6 $ = Millionen
• Potenz von 9 = $ 10 ^ 9 $ = Milliarden
• Potenz von 12 = $ 10 ^ 12 $ = Billionen
• Potenz von 23 = $ 10 ^ 23 $ = Anzahl der Moleküle in einem Dutzend Gramm Kohlenstoff
• Potenz von 80 = $ 10 ^ 80 $ = Anzahl der Moleküle im Universum

Eine Skala von 0 bis 80 führte uns von einem einzelnen Gegenstand zur Anzahl der Dinge im Universum. Nicht zu schäbig.

Logarithmen zählen die Multiplikation als Schritte

Logarithmen beschreiben Änderungen in Bezug auf die Multiplikation: In den obigen Beispielen ist jeder Schritt 10x größer. Mit dem natürlichen Protokoll ist jeder Schritt „e“ (2.71828…) mal mehr.

Wenn es um eine Reihe von Multiplikationen geht, helfen Logarithmen, sie zu „zählen“, genau wie Addition für uns zählt, wenn Effekte addiert werden.

Zeig mir die Mathematik

Zeit für das Fleisch: Mal sehen, wo Logarithmen auftauchen!

Sechsstelliges Gehalt oder 2-stellige Ausgaben

Wir beschreiben Zahlen in Bezug auf ihre Ziffern, d.h. wie viele Potenzen von 10 haben sie (sind sie in den Zehnern, Hunderten, Tausenden, Zehntausenden usw.). Das Hinzufügen einer Ziffer bedeutet „Multiplizieren mit 10“, d.h.

Logarithmen zählen die Anzahl der hinzugefügten Multiplikationen, so dass wir beginnend mit 1 (einer einzelnen Ziffer) 5 weitere Ziffern ($ 10 ^ 5 $) hinzufügen und 100.000 ein 6-stelliges Ergebnis erhalten. Über „6“ anstelle von „Hunderttausend“ zu sprechen, ist die Essenz von Logarithmen. Es gibt ein grobes Maßstabsgefühl, ohne ins Detail zu gehen.

Bonusfrage: Wie würden Sie 500.000 beschreiben? „6-stellig“ zu sagen ist irreführend, da 6-stellig oft etwas näher an 100.000 impliziert. Würde „6.5 figure“ funktionieren?

Nicht wirklich. In unseren Köpfen bedeutet 6,5 „auf halbem Weg“ zwischen 6 und 7 Zahlen, aber das ist die Denkweise eines Addierers. Mit Logarithmen a „.5“ bedeutet auf halbem Weg in Bezug auf die Multiplikation, dh die Quadratwurzel ($ 9 ^.5 $ bedeutet, dass die Quadratwurzel von 9 — 3 in Bezug auf die Multiplikation auf halbem Weg ist, weil es 1 zu 3 und 3 zu 9 ist).

Wenn wir log(500.000) nehmen, erhalten wir 5,7, addieren 1 für die zusätzliche Ziffer und können sagen: „500.000 ist eine 6.7 figurennummer“. Probieren Sie es hier aus:

Größenordnung

Wir Geeks lieben diesen Satz. Es bedeutet ungefähr „10x Unterschied“, klingt aber nur cooler als „1 Ziffer größer“.

In Computern, in denen alles mit Bits (1 oder 0) gezählt wird, hat jedes Bit einen Verdopplungseffekt (nicht 10x). Von 8 auf 16 Bit zu gehen ist also „8 Größenordnungen“ oder $ 2 ^ 8 = 256 $ mal größer. („Größer“ bezieht sich in diesem Fall auf die Speichermenge, die adressiert werden kann.) Von 16 auf 32 Bit bedeutet zusätzliche 16 Größenordnungen oder $ 2 ^ 16 $ ~ 65.536 mal mehr Speicher, der adressiert werden kann.

Zinssätze

Wie ermitteln wir die Wachstumsraten? Ein Land will nicht mit 8,56% pro Jahr wachsen. Sie betrachten das BIP in einem Jahr und das BIP im nächsten Jahr und nehmen den Logarithmus, um die implizite Wachstumsrate zu ermitteln.

Meine zwei Lieblingsinterpretationen des natürlichen Logarithmus (ln(x)), d.h. des natürlichen Logars von 1.5:

• Angenommen, 100% Wachstum, wie lange müssen Sie wachsen, um 1,5 zu erreichen? (.405, weniger als die Hälfte des Zeitraums)
• Angenommen, 1 Zeiteinheit, wie schnell müssen Sie wachsen, um 1,5 zu erreichen? (40.5% pro Jahr, kontinuierlich compoundiert)

Logarithmen sind, wie wir herausfinden, wie schnell wir wachsen.

Messskala: Google PageRank

Google gibt jeder Seite im Web eine Punktzahl (PageRank), die ein grobes Maß für Autorität / Wichtigkeit darstellt. Dies ist eine logarithmische Skala, die in meinem Kopf bedeutet „PageRank zählt die Anzahl der Ziffern in Ihrer Punktzahl“.

Eine Site mit Pagerank 2 („2 Ziffern“) ist also 10x beliebter als eine PageRank 1-Site. Meine Seite ist PageRank 5 und CNN hat PageRank 9, also gibt es einen Unterschied von 4 Größenordnungen ($10^4$ = 10,000).

Grob gesagt bekomme ich ungefähr 7000 Besuche / Tag. Mit meiner Umschlagmathematik kann ich vermuten, dass CNN ungefähr 7000 * 10.000 = 70 Millionen Besuche / Tag erhält. (Wie habe ich das gemacht? In meinem Kopf denke ich $ 7k * 10k = 70 * k * k = 70 * M $). Sie haben vielleicht ein paar Mal mehr (100M, 200M), aber wahrscheinlich nicht bis zu 700M.

Google vermittelt viele Informationen mit einer sehr groben Skala (1-10).

Messung Skala: Richter, Dezibel, etc.

Seufzer. Wir sind bei den typischen „Logarithmen in der realen Welt“ Beispiel: Richterskala und Dezibel. Die Idee ist, Ereignisse, die drastisch variieren können (Erdbeben), auf eine einzige Skala mit einem kleinen Bereich (typischerweise 1 bis 10) zu setzen. Genau wie der PageRank ist jede Erhöhung um 1 Punkt eine 10-fache Verbesserung der Leistung. Das größte von Menschen aufgezeichnete Erdbeben war 9,5; Der Einschlag der Halbinsel Yucatán, der die Dinosaurier wahrscheinlich aussterben ließ, war 13.

Dezibel sind ähnlich, obwohl sie negativ sein können. Geräusche können von intensiv leise (Pindrop) bis extrem laut (Flugzeug) reichen und unser Gehirn kann alles verarbeiten. In Wirklichkeit ist das Geräusch eines Flugzeugtriebwerks Millionen (Milliarden, Billionen) Mal stärker als ein Stecknadelkopf, und es ist unpraktisch, eine Skala von 1 bis zu einer Unmenge zu haben. Logs halten alles in einem vernünftigen Maßstab.

Logarithmische Diagramme

Häufig werden Elemente auf einer „logarithmischen Skala“ dargestellt. In meinem Kopf bedeutet dies, dass eine Seite „Anzahl der Ziffern“ oder „Anzahl der Multiplikationen“ zählt, nicht den Wert selbst. Auch dies hilft dabei, sehr unterschiedliche Ereignisse auf einer einzigen Skala darzustellen (von 1 bis 10, nicht von 1 bis Milliarden).

Moores Gesetz ist ein großartiges Beispiel: wir verdoppeln die Anzahl der Transistoren alle 18 Monate (Bild mit freundlicher Genehmigung von Wikipedia).

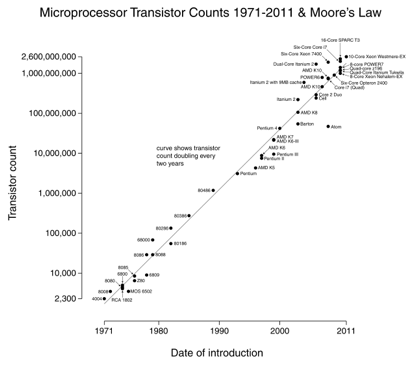
Das Nette an Diagrammen im Protokollmaßstab ist, dass exponentielle Änderungen (Prozessorgeschwindigkeit) als gerade Linie angezeigt werden. Wenn Sie 10x pro Jahr wachsen, steigen Sie stetig auf der „Ziffern“ -Skala auf.

Vorwärts und aufwärts

Wenn ein Konzept bekannt, aber nicht beliebt ist, bedeutet dies, dass wir unsere Intuition aufbauen müssen. Finden Sie die Analogien, die funktionieren, und geben Sie sich nicht mit dem Slop zufrieden, den ein Lehrbuch heraustragen wird. In meinem Kopf:

• Logarithmen finden die Ursache für einen Effekt (siehe Wachstum, Zinssatz finden)
• Sie helfen beim Zählen von Multiplikationen oder Ziffern mit dem Bonus von Teilzählungen (500k ist eine 6,7-stellige Zahl)

Glückliche Mathe.

Andere Beiträge in dieser Serie

1. Ein intuitiver Leitfaden für Exponentialfunktionen & e
2. Entmystifizierung des natürlichen Logarithmus (ln)
3. Ein visueller Leitfaden für einfache, zusammengesetzte und kontinuierliche Zinssätze
4. Gemeinsame Definitionen von e (eingefärbt)
5. Exponenten verstehen (Warum ist 0 ^ 0 = 1?)
6. Verwendung von Logarithmen in der realen Welt
7. Wie man mit Exponenten und Logarithmen denkt
8. Diskretes vs. kontinuierliches Wachstum verstehen
9. Was bedeutet ein Exponent wirklich?
10. Q: Warum ist e spezielle? (2.718…, nicht 2, 3.7 oder eine andere Zahl?)