MO für HF

Molekülorbitale für heterogene zweiatomige Moleküle

Ein einfacher Ansatz zur Molekülorbitaltheorie (MO) für heterogene zweiatomige Moleküle besteht darin, das Energieniveaudiagramm anzuzeigen. Die MO-Energieniveaus können wie folgt berechnet werden:

Denken Sie daran, dass die Energie \(E_n\) für die Quantenzahl n für ein Element mit atomarem Z ungefähr ist

\

Wir verwenden \(Z_{eff}\) anstelle von Z , um zu bedeuten, dass wir die Ordnungszahl modifizieren müssen, um eine effektive Atomladung für den Kern zu erhalten. Da es sich um ungefähre Werte handelt, kann man Z direkt verwenden. Das 1s-Orbitalenergieniveau beträgt -13,6 eV für Wasserstoffatome, gemessen als Ionisationsenergie von H.

Für die Quantenzahl n = 1 beträgt das Energieniveau für 1s von He ungefähr – 54 eV. In ähnlicher Weise ist das 1s-Energieniveau für F – 1101 eV. Das 2s- und 2p-Energieniveau für He beträgt ungefähr – 13,6 eV, was dem von 1s-Orbital von H ähnelt.

Somit beträgt das 2s-Energieniveau für Li ungefähr -6 eV. Für Multielektronenatome haben die p-Subschale und die s-Subschale jedoch aufgrund der Penetration unterschiedliche Energien. Auf dieser Ebene können wir nicht genau sein, sondern denken einfach, dass die 2p-Orbitale eine höhere Energie haben als das 2s-Orbital. Normalerweise überlappen sich Atomorbitale mit ähnlichen Energieniveaus, um Molekülorbitale zu bilden. So passen wir die Energieniveaus von Atomorbitalen an und machen dann Bonding- und Anti-Bonding-MOs von ihnen.

Falls das Energieniveau der Atomorbitale jedoch sehr unterschiedlich ist, verwenden wir Atomorbitale der unvollständigen Unterschale, um MOs zu bilden.

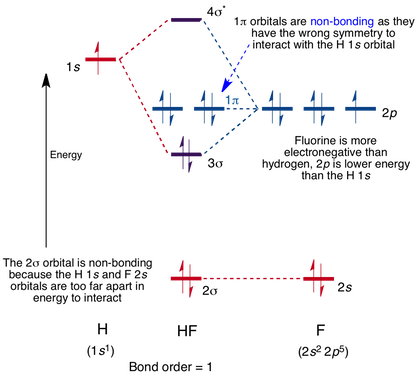
Molekülorbitaldiagramm für das HF-Molekül

Zwischen dem 1s-Orbital auf Wasserstoff und dem 2p-Orbital in Fluor tritt eine Wechselwirkung auf, die die Bildung eines Sigma-bindenden und eines Sigma-antibindenden Molekülorbitals verursacht, wie unten gezeigt.