En cirkel er jævnt opdelt i seks lige trekanter

Hej Marilynn,

først vil jeg fortælle dig mine antagelser om, hvordan dit billede ser ud:

1. hver trekant har et toppunkt (hjørne) i midten af cirklen
2. hver trekant har hjørner på omkredsen af cirklen (så to sider af hver trekant er en radius)
3. trekanterne deler sider (der er ingen gapes mellem trekanter)

det samlede billede ligner en blomst – hver trekant er et kronblad.

det ukendte område er, hvad der er tilbage omkring ydersiden af cirklen, mellem omkredsen og ydersiden af hver trekant. Dette ukendte område er opdelt i seks kongruente sektioner (lige på alle måder – ligesom trekanterne er “lige” på alle måder – inklusive areal, Sidelængde og buelængde). Det er ikke klart, om du mener, at arealet af en bue er Pi (ikke faktisk split Pie, selvom pronouced det samme), eller alle seks sektioner taget sammen er Pi. I det følgende antager jeg, at en af de udvendige sektioner har et område af Pi, så området for alle seks sektioner samlet er 6 gange Pi. Vi skal finde cirkelens radius, kalde den r.

jeg vil også bruge P til at stå for Pi (eller ca. 3.14). Nu er der en masse information, vi kan garnere fra trekanterne:

1. vinklerne i midten er alle 60 grader. Dette skyldes, at de seks vinkler i midten er alle lige, og en cirkel har 360 grader. Så gør 360 uddelt af 6.
2. hver trekant er ligebenet. Dette skyldes, at to sider er ens (de sider, der er en radius).
3. hver trekant er faktisk ligesidet. Fordi det er iscoceles, er de to udvendige vinkler også ens. Men der er 180 grader i en trekant, 60 er allerede brugt i centervinklen, hvilket efterlader 180-60=120 grader for de udvendige vinkler. Men 120 divideret med 2 er 60 grader, så alle tre vinkler er ens, så det er isoscles.
4. hver side i hver trekant er af længde r. Dette skyldes, at vi har 6 kongruente (“lige” på alle måder) ligesidede trekanter, og fordi to sider af hver trekant er en radius.

fra trekantenes geometri skal vi lave noget algebra. Fordi vi kender et område, og vi har brug for en radius, har vi brug for en formel (eller ligning) for radius med hensyn til område (i det følgende skal du huske målet med en formel). Cirkelområdet er P * r2 (r2 betyder R kvadreret, og * betyder multiplicer) arealet af de resterende sektioner uden for trekanterne, men inde i cirklen (et område, vi allerede ikke skal være 6*P), kan også findes ved at trække arealet af trekanterne fra cirkelområdet. Vi skal finde et område af en af de ligesidede trekanter.

Metode 1 til beregning af et areal af en trekant
arealet af en trekant er b*h/2 Det er her, der er brug for noget trigonometri: Tegn en linje fra et toppunkt til en modsat side, der deler den modsatte side i halvdelen og er vinkelret. Dette deler den ligesidede trekant i to kongruente retvinklede trekanter, og den nye side er højden, kalder den h. vi er nødt til at finde h.

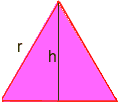
ved hjælp af trig i en af de retvinklede trekanter har vi sin60 = h/R men sin60 = kvm(3)/2, Hvor kvm(3) betyder kvadratroden af tre så kvm(3)/2 = h/r multiplicere begge sider med r for at få h = r*kvm(3)/2 r nu er arealet af en ligesidet trekant b*h/2 = (r)*(r * kvm(3)/2)/2 = (r2)*kvm(3)/4 r = kvm(6*P/(P-6 * kvm(3)/4)) Brug rækkefølgen af operationer til at beregne på en lommeregner (med P=3,14): r= 5,896… Så er cirkelens radius ca. 5.9. Paul