Bootstrap en R

Bootstrap es un método de inferencia sobre una población que utiliza datos de muestra.Bradley Efron lo presentó por primera vez en este papel en 1979.Bootstrap se basa en el muestreo con reemplazo a partir de datos de muestra. Esta técnica se puede utilizar para estimar el error estándar de cualquier estadística y obtener un intervalo de confianza (CI) para ello. Bootstrap es especialmente útil cuando CI no tiene una forma cerrada, o tiene una muy complicada.

Supongamos que tenemos una muestra de n elementos: X = {x1, x2,}, xn} y estamos interesados en CI para alguna estadística T = t (X). Bootstrapframework es sencillo. Simplemente repetimos R veces el siguiente esquema: Para la i-ésima repetición, muestra con elementos de reemplazo n de la muestra disponible (algunos de ellos se recogerán más de una vez). Llame a esta nueva muestra i-ésima muestra de arranque, Xi, y estadística deseada calculada Ti = t (Xi).

Como resultado, obtendremos valores R de nuestra estadística: T1, T2,…, TR. Llamamos a las realizaciones de bootstrap de T o una distribución de bootstrap de T. Basándonos en ella, podemos calcular el CI para T. Hay varias formas de hacer esto. Tomar percentiles parece ser el más fácil.

Bootstrap en acción

Utilicemos (una vez más) el conjunto de datos conocido iris. Eche un vistazo a las primeras filas:

Supongamos que queremos encontrar CIs para la mediana Sepal.Length, medianaSepal.Width y el coeficiente de correlación de rango de Spearman entre estos dos. Usaremos el paquete R ‘ s boot y una función llamada… boot. Para usar su poder, tenemos que crear una función que calcule nuestra(s) estadística (s) a partir de datos remuestreados. Debe tener al menos dos argumentos: a dataset y un vector que contenga indices de elementos de un conjunto de datos que se seleccionaron para crear una muestra de arranque.

Si queremos calcular CIs para más de una estadística a la vez, nuestra función tiene que devolverlos como un único vector.

Para nuestro ejemplo, puede verse así:

library(boot)foo <- function(data, indices){ dt<-data c( cor(dt, dt, method='s'), median(dt), median(dt) )}

foo elige los elementos deseados (cuyos números se almacenan en indices) de data y calcula el coeficiente de correlación de las dos primeras columnas(method='s' se usa para elegir el coeficiente de rango de Spearman,method='p' resultará con el coeficiente de Pearson) y sus medianas.

También podemos añadir algunos argumentos adicionales, por ejemplo. deje que el usuario elija el tipo coeficiente de corrección de odios:

foo <- function(data, indices, cor.type){ dt<-data c( cor(dt, dt, method=cor.type), median(dt), median(dt) )}

Para hacer este tutorial más general, usaré la última versión defoo.

Ahora, podemos usar la función boot. Tenemos que suministrarle un nombre oddataset, función que acabamos de crear, número de repeticiones (R)y cualquier argumento adicional de nuestra función (como cor.type). A continuación, Iuse set.seed para la reproducibilidad de este ejemplo.

set.seed(12345)myBootstrap <- boot(iris, foo, R=1000, cor.type='s')

boot la función devuelve un objeto de la clase llamada… (¡sí, tienes razón!)boot. Tiene dos elementos interesantes. $t contiene valores R de nuestra(s) estadística (es) generada (s) por el procedimiento bootstrap (realizaciones de bootstrap a menudo):

$t0 contiene los valores de nuestras estadísticas en el conjunto de datos original, completo:

myBootstrap$t0## -0.1667777 5.8000000 3.0000000

Imprimir el objeto boot en la consola proporciona más información:

original es lo mismo que $t0. bias es una diferencia entre la media de las realizaciones de bootstrap (las de $t), llamada estimación de bootstrap de T y el valor en el conjunto de datos original (el de $t0).

colMeans(myBootstrap$t)-myBootstrap$t0## 0.002546391 -0.013350000 0.007900000

std. error es un error estándar de la estimación de bootstrap, que equivale a la desviación estándar de las realizaciones de bootstrap.

apply(myBootstrap$t,2,sd)## 0.07573983 0.10295571 0.02726414

Diferentes tipos de CIs de arranque

Antes de comenzar con CI, siempre vale la pena echar un vistazo a la distribución de realizaciones de arranque. Podemos usar la función plot, conindex indicando cuál de las estadísticas calculadas en foo deseamos mirar. Aquí index=1 es un coeficiente de correlación de Spearman entre la longitud y el ancho del tallo, index=2 es una longitud sepal mediana de do, yindex=3 es una anchura sepal mediana de do.

plot(myBootstrap, index=1)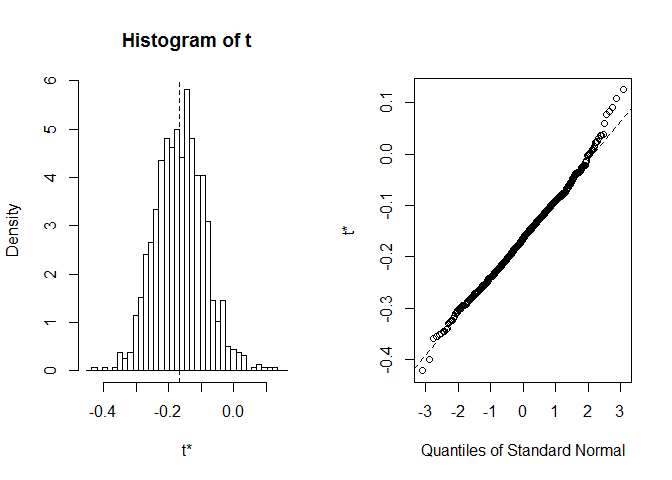

La distribución de los coeficientes de correlación de arranque parece normal. Busquemos a un informante. Podemos usar boot.ci. El valor predeterminado es CIs del 95%, pero se puede cambiar con el parámetro conf.

boot.ci proporciona 5 tipos de CIs de arranque. Uno de ellos, studentizedinterval, es único. Necesita una estimación de la varianza de arranque. No lo proporcionamos, por lo que R imprime una advertencia:bootstrap variances needed for studentized intervals. Las estimaciones de varianza se pueden obtener con bootstrap de segundo nivel o (más fácil) con la técnica de la navaja. Esto está de alguna manera más allá del alcance de este tutorial,así que centrémonos en los cuatro tipos restantes de CIs de arranque.

Si no queremos verlas todas, podemos elegir las relevantes en el argumento type. Los valores posibles son norm, basic, stud, perc, bca ora vector de estos.

La función boot.ci crea un objeto de clase… (sí, lo has adivinado!)bootci. Sus elementos se llaman igual que los tipos de CI utilizados en el argumento type. $norm es un vector de 3 elementos que contiene niveles de confianza y límites de CI.

boot.ci(myBootstrap, index=1, type='norm')$norm## conf ## 0.95 -0.3177714 -0.02087672

$basic, $stud, $perc y $bca son vectores de 5 elementos que contienen también percentiles utilizados para calcular el CI (volveremos a esto más adelante):

boot.ci(myBootstrap, index=1, type='basic')$basic## conf ## 0.95 975.98 25.03 -0.3211981 -0.03285178

Un poco de notación (¡Lo siento!)

Para tener una idea de qué son los diferentes tipos de IC, necesitamos introducir una notación. Así que, vamos:

• t⋆ sea la estimación de arranque (media de las evaluaciones de arranque),
• t0 sea un valor de nuestra estadística en el conjunto de datos original,
• se⋆ sea un error estándar de la estimación de arranque,
• b sea un sesgo de la estimación de arranque b = t⋆ − t0
• α es un nivel de confianza, típicamente α = 0.95,
• a es un quanti 1-\frac \alpha 2 quanti-cuantil de distribución normal estándar,
• θα es un α-percentil de distribución de preparaciones de arranque.

CI percentil

Con la notación anterior, CI percentil es:

(θ (1 − α) / 2, θ1- (1-α)/2)

así que esto solo toma percentiles relevantes. Nada más.

CI normal

Un CI Wald típico sería:

t0 ±a ⋅ se⋆

pero en el caso de arranque, deberíamos corregirlo por sesgo. Por lo tanto, se convierte en:

t t_0 – b \pm z_\alpha \cdot se^\star \\2t_0 – t^\star \pm z_\alpha \cdot se^\star star

CI básico

CI percentil generalmente no se recomienda porque funciona pobremente cuando se trata de distribuciones de cola extraña. El IC básico (también llamado icvotal o empírico) es mucho más sólido para esto. La razón detrás es calcular las diferencias entre cada replicación de bootstrap y t0 y usar percentiles de su distribución. Se pueden encontrar detalles completos, por ejemplo, en All ofStatistics de L. Wasserman

La fórmula final para el CI básico es:

(2t0 − θ1 − (1-α)/2, 2t0-θ(1-α)/2)

BCa CI

BCa proviene de corrección de sesgo, acelerada. La fórmula no es muy complicada, pero algo poco intuitiva, así que la omitiré.Véase el artículo de Thomas J. DiCiccio y Bradleyefron si te interesan los detalles.

La aceleración mencionada en el nombre del método requiere el uso de atributos específicos de realizaciones de arranque. A veces puede suceder que estos sean algunos percentiles extremos, posiblemente valores atípicos.El ACb puede ser inestable en tales casos.

Veamos BCa CI para la mediana de ancho de pétalo. En el conjunto de datos original, esta mediana es exactamente igual a 3.

Obtenemos BCa CI (2,9, 2,9). Eso es raro, pero afortunadamente R nos advirtió que extreme order statistics used as endpoints. Veamos qué pasó exactamente aquí:

plot(myBootstrap, index=3)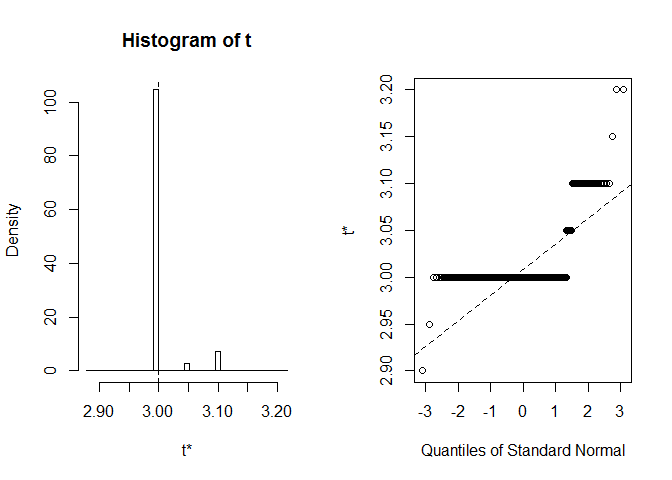

La distribución de realizaciones de bootstrap es inusual. Una gran mayoría de ellos (más del 90%) son 3.

table(myBootstrap$t)#### 2.9 2.95 3 3.05 3.1 3.15 3.2## 1 1 908 24 63 1 2

Replicación de resultados

A veces, necesitamos recrear replicaciones de arranque. Si podemos usar Rpara ello, esto no es un problema. set.seed la función resuelve el problema.Recrear replicaciones de bootstrap en otro software sería mucho más complicado. Además, para R grandes, el recálculo en R tampoco puede ser una opción (por falta de tiempo, por ejemplo).

Podemos lidiar con este problema, guardando índices de elementos del dataset original, que formaron cada muestra de bootstrap. Esto es lo que hace la función boot.array(con argumento indices=T).

tableOfIndices<-boot.array(myBootstrap, indices=T)

Cada fila es una muestra de arranque. Eg., nuestro primer ejemplo contiene los siguientes elementos:

Ajuste indices=F (predeterminado), obtendremos una respuesta a la pregunta «¿Cuántas veces apareció cada elemento del conjunto de datos original en cada muestra de arranque?». Por ejemplo, en la primera muestra: el 1er elemento del conjunto de datos apareció una vez, el 2do elemento no apareció en absoluto, el 3er elemento apareció una vez, el 4to dos veces y así sucesivamente.

Una tabla como esta nos permite recrear la realización de bootstrap fuera de R.O en R cuando no queremos usar set.seed y hacer toda la computación una vez más.

onceAgain<-apply(tableOfIndices, 1, foo, data=iris, cor.type='s')

Comprobemos si los resultados son los mismos:

¡Sí, lo son!

Si desea obtener más información sobre el Aprendizaje automático en R, tome el curso de Herramientas de aprendizaje automático de DataCamp.