Diferencia entre filtros IIR y FIR: una guía práctica de diseño
Un filtro digital es un algoritmo matemático que opera en un conjunto de datos digitales (por ejemplo, datos de sensores) para extraer información de interés y eliminar cualquier información no deseada. Las aplicaciones de este tipo de tecnología incluyen la eliminación de fallos de los datos del sensor o incluso la limpieza del ruido en una señal medida para facilitar el análisis de datos. Pero, ¿cómo elegimos el mejor tipo de filtro digital para nuestra aplicación? ¿Y cuáles son las diferencias entre un filtro IIR y un filtro FIR?
Los filtros digitales se dividen en las dos categorías siguientes:
- Respuesta de impulso infinito (IIR)
- Respuesta de impulso finito (FIR)
Como sugieren sus nombres, cada tipo de filtro se clasifica por la longitud de su respuesta al impulso. Sin embargo, antes de comenzar con un análisis matemático detallado, es prudente apreciar las diferencias en el rendimiento y las características de cada tipo de filtro.
Ejemplo
Para ilustrar las diferencias entre un IIR y un FIR, la respuesta de frecuencia de un FIR de 14o orden (línea continua) y un IIR de tipo I de Chebyshev de 4o orden (línea discontinua) se muestra a continuación en la Figura 1. Observe que aunque los espectros de magnitud tienen un grado similar de atenuación, el espectro de fase del filtro IIR es no lineal en la banda de paso (\(\small 0\rightarrow7.5Hz\)), y se vuelve muy no lineal en la frecuencia de corte, \(\small f_c=7.5 Hz\). Observe también que el FIR requiere un mayor número de coeficientes (15 frente a los 10 del IIR) para que coincida con las características de atenuación del IIR.
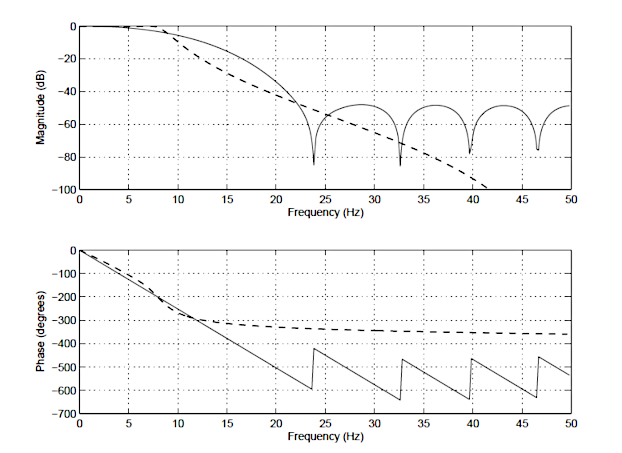
Estas son solo algunas de las diferencias entre los dos tipos de filtros. A continuación se presenta un resumen detallado de las principales ventajas y desventajas de cada tipo de filtro.
Filtros IIR
Los filtros IIR (respuesta de impulso infinito) generalmente se eligen para aplicaciones donde la fase lineal no es demasiado importante y la memoria es limitada. Se han implementado ampliamente en ecualización de audio, procesamiento de señales de sensores biomédicos, sensores inteligentes IoT/IIoT y aplicaciones de telecomunicaciones/RF de alta velocidad.
Ventajas
- Bajo costo de implementación: requiere menos coeficientes y memoria que los filtros FIR para satisfacer un conjunto similar de especificaciones, es decir, frecuencia de corte y atenuación de banda de parada.
- Baja latencia: adecuado para control en tiempo real y aplicaciones de RF de muy alta velocidad en virtud del bajo número de coeficientes.
- Equivalente analógico: Se puede usar para imitar las características de los filtros analógicos utilizando transformaciones de mapeo de planos s-z.
Desventajas
- Características de fase no lineal: Las características de fase de un filtro IIR son generalmente no lineales, especialmente cerca de las frecuencias de corte. Se pueden utilizar filtros de ecualización de paso completo para mejorar las características de la fase de banda de paso.
- Análisis más detallado: Requiere más análisis de escalado y desbordamiento numérico cuando se implementa en punto fijo. La estructura del filtro de forma directa II es especialmente sensible a los efectos de la cuantificación y requiere un cuidado especial durante la fase de diseño.
- Estabilidad numérica: Menos estables numéricamente que sus contrapartes FIR (respuesta de impulso finito), debido a las rutas de retroalimentación.
Filtros FIR
Los filtros FIR (respuesta de impulso finito) generalmente se eligen para aplicaciones donde la fase lineal es importante y hay disponible una cantidad decente de memoria y rendimiento computacional. Tienen un amplio despliegue en aplicaciones de mejora de señales de audio y biomédicas. Su estructura de cero (discutida a continuación) asegura que nunca se vuelvan inestables para ningún tipo de señal de entrada, lo que les da una clara ventaja sobre el IIR.
Ventajas
- Fase lineal: Los abetos se pueden diseñar fácilmente para tener fase lineal. Esto significa que no se introduce distorsión de fase en la señal a filtrar, ya que todas las frecuencias se desplazan en el tiempo en la misma cantidad, manteniendo así sus relaciones armónicas relativas (es decir, grupo constante y retardo de fase). Este no es el caso de los filtros IIR, que tienen una característica de fase no lineal.
- Estabilidad: Los abetos no utilizan valores de salida anteriores para calcular su salida actual, p. ej. no tienen retroalimentación, nunca pueden volverse inestables para cualquier tipo de señal de entrada, lo que les da una clara ventaja sobre los filtros IIR.
- Respuesta de frecuencia arbitraria: La función firarb() de Parks-McClellan y ASN FilterScript permite el diseño de un FIR con una respuesta de magnitud arbitraria. Esto significa que un ABETO se puede personalizar más fácilmente que un IIR.
- Rendimiento en puntos fijos: los efectos de la cuantificación son menos graves que los de un IIR.
Desventajas
- Alto requerimiento computacional y de memoria: Los abetos generalmente requieren muchos más coeficientes para lograr un corte agudo que sus contrapartes IIR. La consecuencia de esto es que requieren mucha más memoria y una cantidad significativamente mayor de operaciones MAC (múltiples y acumuladas). Sin embargo, las arquitecturas modernas de microcontroladores basadas en los núcleos Cortex-M de Arm ahora incluyen soporte de hardware DSP a través de SIMD (instrucción de señal, datos múltiples) que aceleran significativamente la operación de filtrado.
- Latencia más alta: el mayor número de coeficientes significa que, en general, un FIR es menos adecuado que un IIR para aplicaciones de alto rendimiento rápido. Esto se vuelve problemático para aplicaciones de control de bucle cerrado en tiempo real, donde un filtro FIR puede tener demasiado retraso de grupo para lograr la estabilidad del bucle.
- Sin equivalente analógico: utilizando la transformación z combinada bilineal (mapeo s-z), un filtro analógico se puede transformar fácilmente en un filtro IIR equivalente. Sin embargo, esto no es posible para un FIR, ya que no tiene equivalente analógico.
Definiciones matemáticas
Como se explica en la introducción, el nombre IIR y FIR se originan de las definiciones matemáticas de cada tipo de filtro, es decir, un filtro IIR se clasifica por su respuesta de impulso teóricamente infinita,
y(n)=\sum_{k=0}^{\infty}h (k)x (n-k)
\)
y un ABETO categorizado por su respuesta de impulso finito,
y (n) = \sum_{k = 0}^{N-1}h (k) x (n-k)
\)
Ahora analizaremos las propiedades matemáticas de cada tipo de filtro a su vez.
Definición IIR
Como se ha visto anteriormente, un filtro IIR se clasifica por su respuesta de impulso teóricamente infinita,
\(\displaystyle y(n)=\sum_{k=0}^{\infty}h(k)x (n-k) \)
Prácticamente hablando, no es posible calcular la salida de un IIR usando esta ecuación. Por lo tanto, la ecuación puede reescribirse en términos de un número finito de polos \(\small p\) y ceros \(\small q\), como se define por la ecuación de diferencia de coeficiente constante lineal dada por:
y(n)= \ sum_{k=0}^{q}b_k x(n-k) – \sum_{k = 1}^{p}a_ky (n-k)
\)
donde, \(\small a_k\) y \(\small b_k\) son los coeficientes polinómicos del denominador y numerador del filtro, cuyas raíces son iguales a los polos y ceros del filtro respectivamente. Por lo tanto, se puede definir una relación entre la ecuación de diferencia y la transformación z (función de transferencia) mediante el uso de la propiedad de retardo de transformación z de tal manera que,
\sum_{k=0}^{q}b_kx(n-k)-\sum_{k=1}^{p}a_ky(n-k)\quad\stackrel{\displaystyle\mathcal{Z}}{\longleftrightarrow}\quad\frac{\sum\limits_{k=0}^q b_kz^{- k}}{1 + \sum \ limits_{k = 1}^p a_kz^{- k}}
\)
Como se ha visto, la función de transferencia es una representación de dominio de frecuencia del filtro. Observe también que los polos actúan sobre los datos de salida, y los ceros sobre los datos de entrada. Dado que los polos actúan sobre los datos de salida y afectan a la estabilidad, es esencial que sus radios permanezcan dentro del círculo de la unidad (es decir, <1) para la estabilidad de BIBO (entrada acotada, salida acotada). Los radios de los ceros son menos críticos, ya que no afectan la estabilidad del filtro. Esta es la razón principal por la que los filtros FIR (respuesta de impulso finito) totalmente nulos siempre son estables.
Estabilidad de BIBO
Un sistema lineal invariante en el tiempo (LTI) (como un filtro digital) se dice que es entrada acotada, salida acotada estable o BIBO estable, si cada entrada acotada da lugar a una salida acotada, como
\(\displaystyle \sum_{k=0}^{\infty}\left|h(k)\right|<\infty \)
Donde, \(\small h(k)\) es la respuesta de impulso del sistema LTI. Al analizar esta ecuación, debe quedar claro que el criterio de estabilidad de BIBO solo se cumplirá si los polos del sistema se encuentran dentro del círculo unitario, ya que la ROC (región de convergencia) del sistema debe incluir el círculo unitario. En consecuencia, es suficiente decir que una señal de entrada acotada siempre producirá una señal de salida acotada si todos los polos se encuentran dentro del círculo de la unidad.
Los ceros, por otro lado, no están limitados por este requisito, y como consecuencia pueden estar en cualquier lugar del plano z, ya que no afectan directamente la estabilidad del sistema. Por lo tanto, se puede realizar un análisis de estabilidad del sistema calculando en primer lugar las raíces de la función de transferencia (es decir, las raíces de los polinomios numerador y denominador) y luego trazando los polos y ceros correspondientes sobre el plano z.
Una situación interesante surge si hay algún polo en el círculo unitario, ya que se dice que el sistema es marginalmente estable, ya que no es estable o inestable. Aunque los sistemas marginalmente estables no son BIBO estables, han sido explotados por diseñadores de osciladores digitales, ya que su respuesta de impulso proporciona un método simple de generación de ondas sinusoidales, que han demostrado ser invaluables en el campo de las telecomunicaciones.
Filtros Biquad IIR
Se dice que la implementación del filtro IIR discutida aquí es biquad, ya que tiene dos polos y dos ceros, como se ilustra a continuación en la Figura 2. La implementación de biquad es particularmente útil para implementaciones de punto fijo, ya que los efectos de cuantización y estabilidad numérica se minimizan. Sin embargo, el éxito general de cualquier implementación de biquad depende de la precisión numérica disponible, que debe ser suficiente para garantizar que los polos cuantificados estén siempre dentro del círculo unitario.
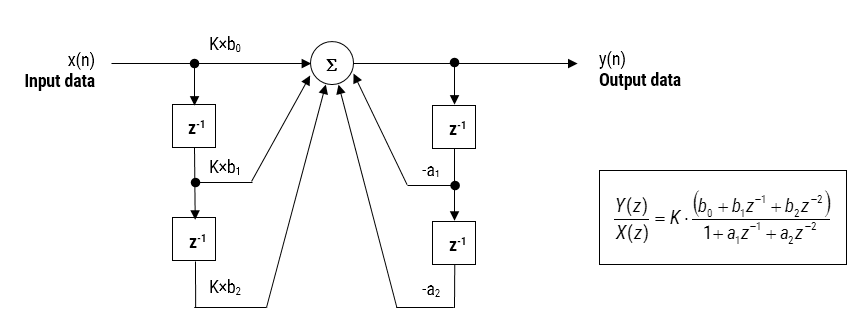
Figura 2: Función de realización y transferencia de filtros IIR de forma directa I (biquad).
Analizando la Figura 2, se puede ver que la estructura biquad en realidad está compuesta por dos rutas de retroalimentación (escaladas por \(\small a_1\) y \(\small a_2\)), tres rutas de avance de alimentación (escaladas por \(\small b_0, b_1\) y \(\small b_2\)) y una ganancia de sección, \(\small K\). Por lo tanto, la operación de filtrado de la Figura 1 se puede resumir mediante la siguiente ecuación recursiva simple:
\(\displaystyle y(n)=K\times \ Big – a_1 y(n-1)-a_2 y(n-2)\)
Analizando la ecuación, observe que la implementación de biquad solo requiere cuatro adiciones (que requieren solo un acumulador)y cinco multiplicaciones, que se pueden acomodar fácilmente en cualquier microcontrolador Cortex-M. La ganancia de sección, \(\small K\) también puede multiplicarse previamente con los coeficientes de trayectoria hacia adelante antes de la implementación.
Una colección de filtros Biquad se conoce como Cascada Biquad, como se ilustra a continuación.

El Diseñador de filtros ASN puede diseñar e implementar una cascada de hasta 50 biquads (solo edición profesional).
Implementación de punto flotante
Al implementar un filtro en punto flotante (es decir, utilizando aritmética de precisión doble o simple), las estructuras de Forma Directa II se consideran una mejor opción que la estructura de Forma Directa I. La estructura transpuesta de la Forma Directa II se considera la más precisa numéricamente para la implementación de coma flotante, ya que los efectos indeseables del swamping numérico se minimizan al analizar las ecuaciones de diferencia.
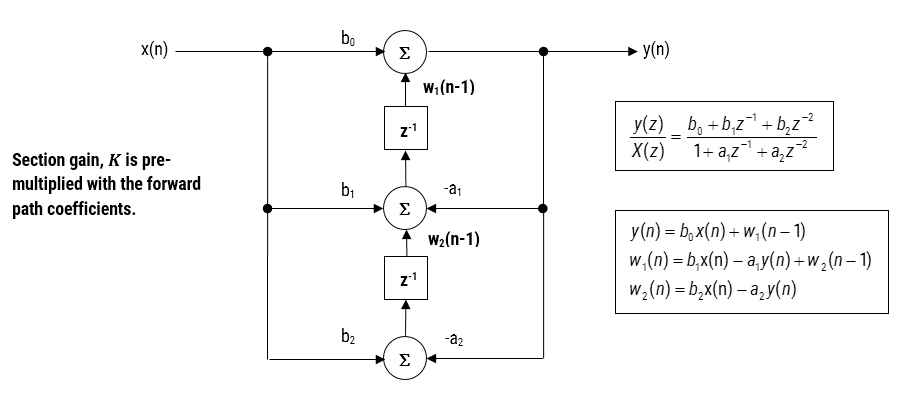
Figura 3-Estructura transpuesta de Forma Directa II, función de transferencia y ecuaciones de diferencia
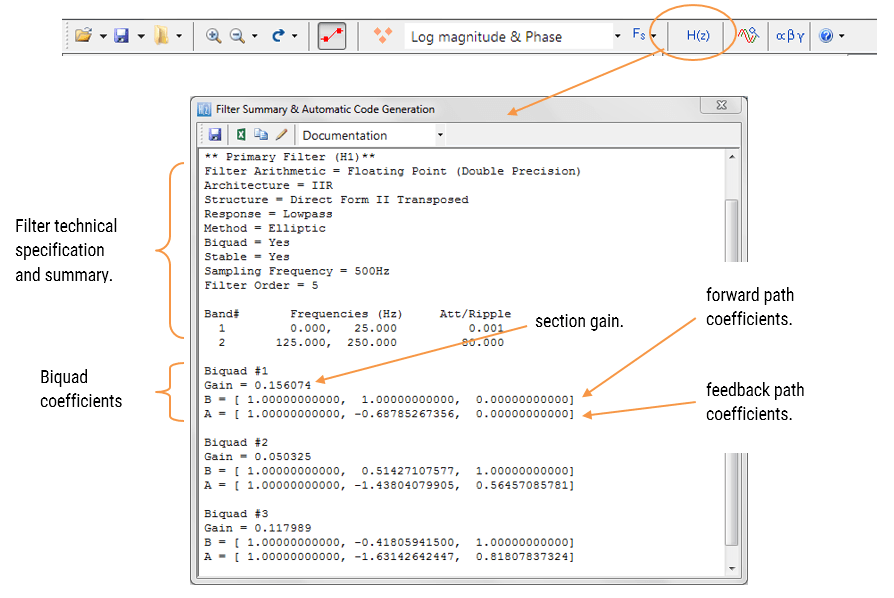
El resumen del filtro (que se muestra en la Figura 4) proporciona al diseñador una descripción detallada del filtro diseñado, que incluye un resumen detallado de las especificaciones técnicas y los coeficientes del filtro, que presenta una ruta rápida y sencilla para documentar su diseño.
El Diseñador de filtros ASN admite el diseño y la implementación de filtros IIR de sección única y Biquad (configuración predeterminada).
Definición FIR
Devolver la ecuación de diferencia de coeficiente constante lineal del IIR, es decir,
y (n) = \sum_{k = 0}^{q} b_kx (n-k) – \sum_{k = 1}^{p}a_ky (n-k)
\)
Observe que cuando establecemos los coeficientes \(\small a_k\) (es decir, la retroalimentación) a cero, la definición reduce a nuestra definición original de filtro de ABETO, lo que significa que el cálculo de ABETO se basa solo en valores de entrada pasados y presentes, a saber:
y (n) = \sum_{k = 0}^{q} b_kx (n-k)
\)
Implementación
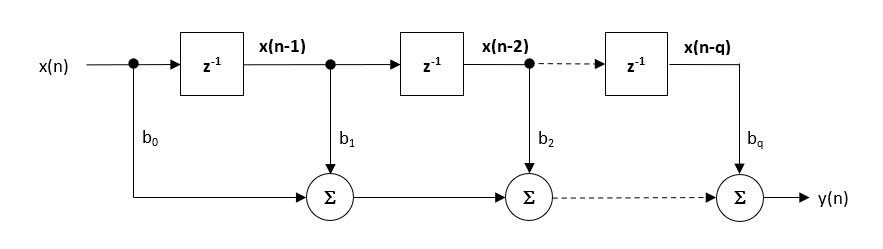
Aunque existen varias implementaciones prácticas para FIRs, la estructura de forma directa y su primo transpuesto son quizás las más utilizadas, y como tal, todos los coeficientes de filtro diseñados están destinados a la implementación en una estructura de forma directa.
La estructura de forma directa y la ecuación de diferencia asociada se muestran a continuación. La Forma Directa es defendida para la implementación de punto fijo en virtud del concepto de acumulador único.
\(\displaystyle y(n) = b_0x (n) + b_1x (n-1) + b_2x (n-2) + …. +b_qx (n-q) \)
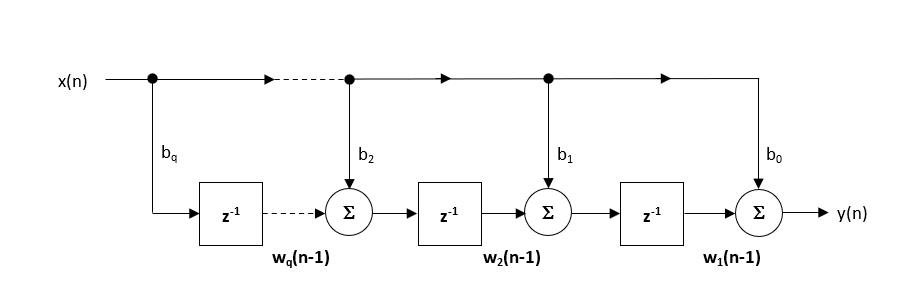
La estructura recomendada (predeterminada) dentro del Diseñador de filtros ASN es la estructura Transpuesta de forma directa, ya que ofrece una precisión numérica superior cuando se usa aritmética de coma flotante. Esto se puede ver fácilmente mediante el análisis de las ecuaciones de diferencia a continuación (utilizadas para la implementación), ya que los efectos indeseables de la inundación numérica se minimizan, ya que la adición de coma flotante se realiza en números de magnitud similar.
\(\displaystyle \begin{eqnarray}y(n) & = &b_0x(n) &+& w_1(n-1) \\ w_1(n)&=&b_1x(n) &+& w_2(n-1) \\ w_2(n)&=&b_2x(n) &+& w_3(n-1) \\ \vdots\quad &=& \quad\vdots &+&\quad\vdots \\ w_q(n)&=&b_qx(n) \end{eqnarray}\)
¿Qué hemos aprendido?
Los filtros digitales se dividen en las dos categorías siguientes:
- Respuesta de impulso infinito (IIR)
- Respuesta de impulso finito (FIR)
Los filtros IIR (respuesta de impulso infinito) generalmente se eligen para aplicaciones donde la fase lineal no es demasiado importante y la memoria es limitada. Se han implementado ampliamente en ecualización de audio, procesamiento de señales de sensores biomédicos, sensores inteligentes IoT/IIoT y aplicaciones de telecomunicaciones/RF de alta velocidad.
Los filtros FIR (respuesta de impulso finito) generalmente se eligen para aplicaciones donde la fase lineal es importante y hay una cantidad decente de memoria y rendimiento computacional disponibles. Tienen un amplio despliegue en aplicaciones de mejora de señales de audio y biomédicas.
ASN Filter Designer proporciona a los ingenieros todo lo que necesitan para diseñar, experimentar e implementar filtros digitales IIR y FIR complejos para una variedad de aplicaciones de medición de sensores. Estas ventajas, junto con la documentación automática y la funcionalidad de generación de código, permiten a los ingenieros diseñar y validar un filtro digital IIR/FIR en minutos en lugar de horas.
