El Sistema Solar: La Tierra y la Luna
Los planetas están alejados de nosotros a decenas y a cientos de millones de kilómetros. Para evitar la utilización de unos números tan grandes se adopta como unidad de distancia la Unidad Astronómica (UA), es decir, la distancia media entre la Tierra y el Sol, 149,600,000 km. La luz tarda en cubrir esta distancia 8 minutos y 19 segundos.
El tamaño del Sistema Solar sobrepasa la órbita de Plutón situado a 40 UA y se define como aquél en el que la fuerza de atracción del Sol se iguala a la fuerza de atracción de las estrellas más próximas a nosotros. Las dimensiones del sistema Solar serían entonces del orden de 1.5 105 UA. Evidentemente, estas dimensiones son muy pequeñas comparadas con las dimensiones de la galaxia o del Universo visible. Las unidades que se toman para medir esas enormes distancias son el año-luz y el parsec que equivale a 206 265 UA o bien, a 3.26 años-luz.
Los planetas del Sistema Solar se dividen en dos grupos: el grupo terrestre formado por Mercurio, Venus, la Tierra y Marte y el grupo de los planetas gigantes formado por Júpiter, Saturno, Urano y Neptuno.
Todos los planetas salvo Venus y Mercurio tienen satélites, la mayor parte de los cuales pertenece a los planetas gigantes. La Tierra, Júpiter, Saturno y Neptuno tienen los satélites más grandes: la Luna, los satélites de Júpiter descubiertos por Galileo (Io, Europa, Ganímedes, Calisto), el satélite Titán de Saturno y Tritón de Neptuno.
Los asteroides ocupan una vasta región anular situada entre las órbitas de Marte y Júpiter, a una distancia media de 2.75 UA del Sol. El asteroide más grande es Ceres que tiene un diámetro de 1000 km.
Los cometas, se han catalogado unos 600, se dividen en dos grupos, de periodo corto (menor de 20 años) y de periodo largo (mayor de 20 años). Existen diversas hipótesis acerca del origen de los cometas entre la que figura la del astrónomo holandés J. Oort.
Además de los cuerpos citados en el espacio interplanetario, existe gran cantidad de partículas de tamaños diferentes, predominado aquellas que tienen una masa de milésimas o millonésimas de gramo, que se denominan polvo meteórico. La formación de estas partículas se debe probablemente al choque de cuerpos más grandes (asteroides) y a su fragmentación sucesiva a lo largo de la existencia y evolución del Sistema Solar.
Al polvo meteórico se debe el fenómeno de la luz zodiacal, que se observa después de anochecer o antes del amanecer, debido a la dispersión de la luz por estas partículas de polvo. La mayoría de las partículas se evapora al entrar en la atmósfera terrestre (a alturas entre 80 a 120 km), solamente una pequeña proporción llega a la superficie terrestre.
Veamos ahora algunos datos relativos a los planetas del Sistema Solar
Primero del Sol
| Cuerpo celeste | Radio | Masa |
|---|---|---|
| Sol | 6.96·108 m | 1.98·1030 kg |
Luego, de la Tierra
| Cuerpo celeste | Semieje mayor | Periodo | Masa |
|---|---|---|---|
| Tierra | 149.6·109 m | 1 año=365.26 días | 5.98·1024 kg |
y del resto de los planetas
| Planeta | Semieje mayor (UA) | Excentricidad | Periodo (años) | Masa |
|---|---|---|---|---|
| Mercurio | 0.387 | 0.206 | 0.24 | 0.06 |
| Venus | 0.723 | 0.007 | 0.62 | 0.82 |
| Tierra | 1.000 | 0.017 | 1.00 | 1.00 |
| Marte | 1.524 | 0.093 | 1.88 | 0.11 |
| Júpiter | 5.203 | 0.048 | 11.86 | 318 |
| Saturno | 9.539 | 0.056 | 29.46 | 95.1 |
| Urano | 19.182 | 0.047 | 84.01 | 14.6 |
| Neptuno | 30.058 | 0.009 | 164.8 | 17.2 |
En la siguiente tabla se proporcionan datos complementarios:
- La inclinación del plano de la órbita del planeta respecto de la eclíptica (plano de la órbita de la Tierra)
- El periodo de rotación alrededor de su eje. Ha sido muy complicado medir esta magnitud para planetas como Mercurio y Venus. Las envolturas gaseosas de Júpiter, Saturno, Urano y Neptuno poseen la propiedad de la rotación diferencial, es decir, sus periodos de rotación varía según la latitud.
- La inclinación del eje de rotación respecto del plano de la órbita. En el caso de Venus es de 177º que equivale a decir que la inclinación del eje es de 3º pero el sentido de la rotación es inverso. El mismo argumento vale para Urano, lo que indica que el eje de rotación de Urano está casi en el plano de su órbita.
| Planeta | Inclinación de la órbita | Periodo de rotación | Densidad g/cm3 | Radio ecuatorial (km) | Inclinación del eje | Nº de satélites |
|---|---|---|---|---|---|---|
| Mercurio | 7º.0 | 58d.6 | 5.44 | 2 439 | <30º | 0 |
| Venus | 3º.4 | 243d | 5.24 | 6 051 | 177º | 0 |
| Tierra | 0º | 23h.9 | 5.52 | 6 378 | 23º.5 | 1 |
| Marte | 1º.8 | 24h.6 | 3.95 | 3 394 | 25º.2 | 2 |
| Júpiter | 1º.3 | 9h.9 | 1.33 | 71 398 | 3º.1 | 16 |
| Saturno | 2º.5 | 10h.2 | 0.69 | 60 000 | 26º.4 | 17 |
| Urano | 0º.8 | 10h.8 | 1.26 | 25 400 | 98º | 5 |
| Neptuno | 1º.8 | 15h.8 | 1.67 | 24 750 | 29º | 2 |
Los satélites
Finalmente, proporcionamos algunos datos relativos a los principales satélites de los planetas. Júpiter y Saturno tienen muchos satélites cuyo tamaño es mucho mayor que los de Marte, pero solamente mencionamos aquellos que tienen un tamaño similar o mayor que nuestra Luna.
| Planeta | Satélites | Densidad g/cm3 | Radio medio (km) | Radio órbita (103 km) | Periodo (días) |
|---|---|---|---|---|---|
| Tierra | Luna | 3.33 | 1 738 | 384.4 | 27.32 |
| Marte | Fobos | 2.1 | 13.5 | 9.38 | 0.319 |
| Deimos | 2.1 | 7.5 | 23.46 | 1.262 | |
| Júpiter | Io | 3.53 | 1 820 | 421.6 | 1.769 |
| Europa | 3.03 | 1 565 | 670.9 | 3.551 | |
| Ganimedes | 1.93 | 2 638 | 1 070 | 7.155 | |
| Calisto | 1.83 | 2 410 | 1 880 | 16.689 | |
| Saturno | Titán | 1.9 | 2 575 | 1 221.9 | 15.95 |
| Neptuno | Tritón | 2 200 | 394.7 | 5.84 |
Actividades
- Determinar la masa del planeta Júpiter a partir de los datos del radio y del periodo de revolución de uno de sus satélites.
- Determinar el radio de la órbita de un satélite del planeta Júpiter a partir de la masa de dicho planeta y del periodo de revolución del satélite.
- Determinar la intensidad del campo gravitatorio g en la superficie de los planetas y algunos satélites, a partir de los datos de su masa M y su radio R o bien, de su densidad ρ y de su radio.
Ejemplo: determinar la masa del planeta Júpiter sabiendo que el radio de la órbita de Io es de 421 600 km y que su periodo de revolución es de 1.769 días. Dato: la constante G vale 6.67·10-11 Nm2/kg2
Ejemplo: Calcular el radio de la órbita del satélite Calisto sabiendo que su periodo de revolución es de 16.689 días y la masa del planeta Júpiter es de 1.901·1027 kg. Dato: la constante G vale 6.67·10-11 Nm2/kg2
g=G M R 2 = 4π 3 GρR
Dato: la constante G vale 6.67·10-11 Nm2/kg2
La Luna
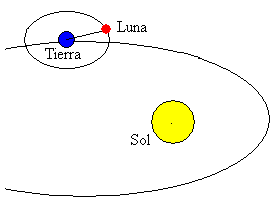
La Luna es uno de los cuerpos más grandes del sistema Solar. Su órbita es casi circular (excentricidad ε=0.05) y el plano de su órbita está inclinado 5º respecto del plano de la órbita de la Tierra.
La distancia media entre el centro de la Tierra y la Luna es de 384 400 km. Su periodo de rotación alrededor de la Tierra es de 27.322 días. El cambio de la posición de la Luna con respecto del Sol da lugar a las fases de la Luna.
La Luna siempre presenta la misma cara al observador terrestre, debido al efecto de las fuerzas de marea que ejerce la Tierra sobre la Luna. Lo cual significa, que coincide el periodo de rotación de la Luna alrededor de su eje y el tiempo que tarda en completar una órbita alrededor de la Tierra.
La Luna es el objeto celeste que más ha fascinado a la especie humana. La antigua Unión Soviética envió por primera vez una nave automática que se posó en la superficie de la Luna el año 1959. El 20 de Julio de 1969 Neil Armstrong acompañado de Edwin Aldrin fueron los primeros hombres que caminaron sobre la superficie de la Luna en el marco de la misión Apollo 11. La última visita de los astronautas americanos a la Luna tuvo lugar en el año 1972.
El origen de la Luna parece incierto, hay varias teorías:
-
Que se formó al mismo tiempo que la Tierra con el material procedente de una nebulosa
-
Que un cuerpo celeste se dividió en dos partes dando origen a la Tierra y a la Luna
-
Que la Luna se formó en otro lugar y fue capturada por la Tierra
-
Que la Tierra colisionó con un objeto celeste de gran tamaño (del tamaño de Marte o mayor) y que la Luna se formó con el material expulsado de esta colisión.
La última teoría, parece, de momento, la más aceptada por la comunidad científica.
Trayectoria de la Luna
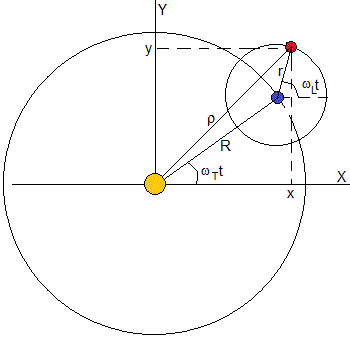
Consideremos un planeta y su satélite. El planeta describe una órbita circular de radio R alrededor de su estrella con velocidad angular constante ωT=2π/PT, siendo PT el periodo o tiempo que trada en dar una vuelta completa. El satélite describe una órbita circular coplanaria de radio r con velocidad angular constante ωL=2π/PL, siendo PL el periodo o tiempo que tarda en dar una vuelta completa
La posición del satélite respecto de un sistema de referencia cuyo origen es la estrella, es
x=Rcos( ω T t )+rcos( ω L t ) y=Rsin( ω T t )+rsin( ω L t )
Sea α=ωT/ωL
{ x=Rcos( α ω L t )+rcos( ω L t ) y=Rsin( α ω L t )+rsin( ω L t ) { x=Rcos( α 2π P L t )+rcos( 2π P L t ) y=Rsin( α 2π P L t )+rsin( 2π P L t )
Llamemos τ=t/PL
x R =cos( α·2πτ )+ r R cos( 2πτ ) y R =sin( α·2πτ )+ r R sin( 2πτ )
Representamos la trayectoria de un satélite para α=0.1 y para tres valores del cociente r/R.
- r/R<α. Ejemplo, r/R=0.05
- r/R=α. Ejemplo, r/R=0.1
- r/R>α. Ejemplo, r/R=0.15
alfa=0.1;r=0.15;fplot(@(t) r*cos(2*pi*t)+cos(2*pi*alfa*t), @(t) r*sin(2*pi*t)+sin(2*pi*alfa*t),)text(0.1,0.1,sprintf('\alpha=%1.2f',alfa))text(0.1,0.2,sprintf('r/R=%1.2f',r))axis equalgrid onxlabel('x/R')ylabel('y/R')title('Trayectoria de un satélite')
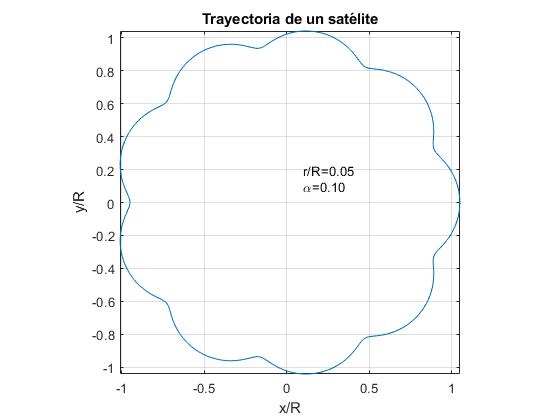
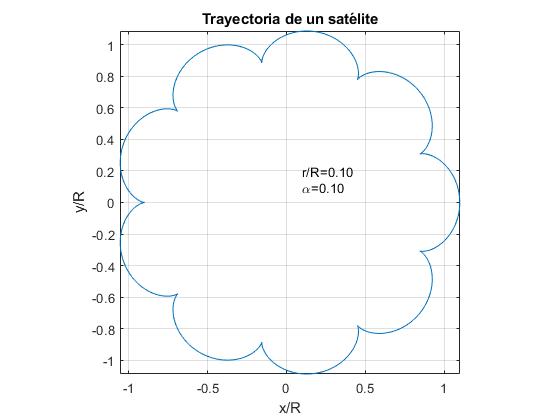
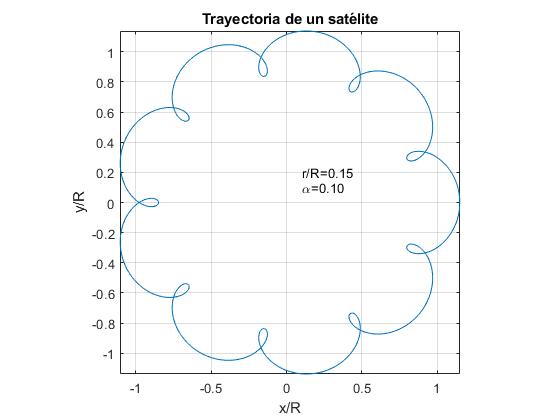
Para el caso de la Tierra y la Luna, los datos son:
- radio de la órbita de la Luna: r=384.4·106 m, periodo PL=27.32 d
- radio de la de la órbita de la Tierra: R=149.6·109 m, periodo PT=365.26 d
α=ωT/ωL=PL/PT=0.0748. r/R=0.0026
La órbita de la Luna se parecerá a la primera figura. En la representación gráfica de la trayectoria de la Luna para estos valores de α y r/R no se aprecian las oscilaciones de la distancia radial entre el Sol y la Luna
Aceleración de la Luna
La distancia ρ desde el Sol a la Luna es
ρ 2 = x 2 + y 2 = R 2 + r 2 +2rRcos( ( ω L − ω T )t )
Calculamos las componentes rectangulares de la aceleración
{ dx dt =− ω T Rsin( ω T t )− ω L rsin( ω L t ) dy dt = ω T Rcos( ω T t )+ ω L rcos( ω L t ) { a x = d 2 x d t 2 =− ω T 2 Rcos( ω T t )− ω L 2 rcos( ω L t ) a y = d 2 y d t 2 =− ω T 2 Rsin( ω T t )− ω L 2 rsin( ω L t )
La componente radial de la aceleración
a ρ = a → · ρ → ρ = a x x+ a y y x 2 + y 2 =− ω T 2 R 2 + ω L 2 r 2 +( ω T 2 + ω L 2 )Rrcos( ( ω L − ω T )t ) R 2 + r 2 +2rR cos( ( ω L − ω T )t )
Los valores máximo y mínimo se obtienen cuando cos((ωL-ωT)t)=±1
a máx =− ω T 2 R 2 + ω L 2 r 2 +( ω T 2 + ω L 2 )Rr R 2 + r 2 +2rR =−( ω T 2 R+ ω L 2 r ) a mín =− ω T 2 R 2 + ω L 2 r 2 −( ω T 2 + ω L 2 )Rr R 2 + r 2 −2rR =−( ω T 2 R− ω L 2 r )
>> R=149.6e9; %Tierra>> r=384.4e3; %Luna>> wT=2*pi/(365*24*60*60) %velocidad angular TierrawT = 1.9924e-07>> wL=2*pi/(27.32*24*60*60) %velocidad angular TierrawL = 2.6619e-06>> aM=-(wT^2*R+wL^2*r)aM = -0.0059>> am=-(wT^2*R-wL^2*r)am = -0.0059
La Luna es el único satélite del Sistema Solar, cuya componente radial de la aceleración es negativa, se dice que ‘la Luna cae hacia el Sol’
Las fases de la Luna
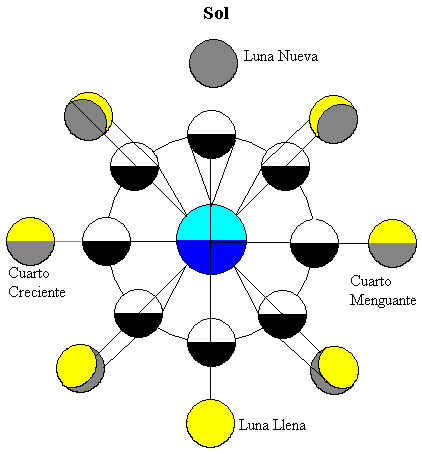
La figura muestra la Luna en diferentes posiciones de su órbita alrededor de la Tierra. El Sol está muy alejado iluminando a ambos cuerpos celestes (en la parte superior de la figura)
La mitad de la Luna está iluminada por el Sol (en color blanco) y la mitad de la Luna más cercana a la Tierra es visible por observador terrestre. A medida que la Luna se mueve alrededor de la Tierra vemos distintas fracciones de la parte iluminada por el Sol (las zonas en color amarillo).
-
Cuando la Luna está entre la Tierra y el Sol, la parte de la Luna más cercana a la Tierra está oscura, por lo que no podemos ver la Luna, a esta fase se denomina Luna Nueva.
-
Cuando la Tierra está entre el Sol y la Luna, la parte de la Luna más cercan a la Tierra es la mitad iluminada, se denomina a esta fase Luna Llena.
-
Cuando la Luna está en posiciones intermedias, solamente la mitad de la parte más cercana a la Tierra está iluminada. Por tanto, solamente vemos un cuarto de la Luna, a estas dos fases se le denominan Cuartos, Creciente o Menguante dependiendo si la parte iluminada que es visible desde la Tierra tiende a crecer o a decrecer.
Nota: Este programa interactivo intenta explicar las fases de la Luna, pero no es una representación fiel de la órbita de la Luna, que forma un ángulo de 5º con el plano de la eclíptica (de la órbita de la Tierra alrededor del Sol), ni de la orientación del eje de la Tierra que forma aproximadamente 23º con la normal al plano de la eclíptica.
Se ha dibujado una línea de color rojo que atraviesa la Luna para que el lector aprecie la coincidencia del periodo de rotación de la Luna alrededor de su eje y el tiempo que tarda en completar una órbita alrededor de la Tierra y por tanto, la Luna presenta siempre la misma cara a la Tierra.
Eclipses de la Luna
Los eclipses de Luna se producen siempre que la Luna esté en fase Llena y siempre que el Sol, la Tierra y la Luna estén en línea recta. Entonces la Luna se encuentra en la sombra producida por la Tierra tal como se muestra en la figura.
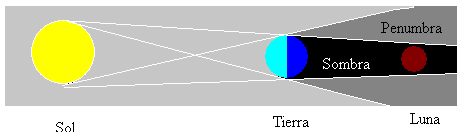
Hay otros tipos de eclipse lunares, que dependen del alineamiento de los tres cuerpos celestes. La Luna puede encontrase en zona no iluminada (sombra) o parcialmente iluminada (penumbra).
El eclipse Solar se produce cuando la Luna se interpone entre el Sol y la Tierra, la Luna está en fase Nueva. La Luna es 400 veces más pequeña que el Sol pero la Luna está 400 veces más cercana a la Tierra, por tanto, el tamaño aparente de ambos cuerpos vistos desde la Tierra es casi el mismo. La Luna puede de esta manera, producir un eclipse total del Sol, si es observado en la zona de sombra proyectada por la Luna sobre la Tierra.
Datos de la Luna
| Masa (kg) | 7.349·1022 |
| Radio (km) | 1737. 4 |
| Densidad media (g/cm3) | 3.34 |
| Distancia media a la Tierra (km) | 384 000 |
| Periodo de orbital (días) | 27.32166 |
| Aceleración de la gravedad en el ecuador (m/s2) | 1.62 |
| Excentricidad de la órbita | 0.0549 |
| Inclinación de la órbita (grados) | 5.1454 |
-
Calcular el radio de la órbita circular de la Luna alrededor de la Tierra sabiendo que el periodo es 27.32 días. Calcular también la velocidad de la Luna. Datos: G =6.67·10-11 Nm2/kg2, la masa de la Tierra es M=5.98·1024 kg.
-
Calcular la aceleración de la gravedad g en la superficie de la Luna.
-
Calcular el cociente entre el diámetro del Sol y el diámetro de la Luna. Calcular la relación entre la distancia media entre el Sol y la Tierra, y la Luna y la Tierra. Datos: radio del Sol 6.96·108 m, distancia media Tierra-Sol 1.49·1011 m
-
Calcular la posición del centro de masa del sistema Tierra-Luna, medido desde el centro de la Tierra.
-
Calcular la fuerza de atracción de la Tierra sobre la Luna, compararla con la fuerza de atracción del Sol sobre la Luna. Dato: masa del Sol, 1.98·1030 kg
Referencias
M. Márov. Planetas del Sistema Solar. Editorial Mir.
Más información acerca de los planetas en ¿Cuántos planetas hay en nuestro Sistema Solar?. ComofuncionaQue.com
Para el apartado ‘Trayectoria de la Luna’
David C. Johnston. Cycloidal paths in physics as superpositions of translational and rotational motions. Am. J. Phys.87(10), Octubre de 2019, pp.808-810
La Luna Siempre Gira Hacia el Sol. Páginas de matemáticas.