Fundamentos de la Epidemiología
Después de leer este capítulo, podrá hacer lo siguiente:
- Explicar qué es la modificación de efectos
- Diferenciar entre factores de confusión y modificadores de efectos
- Realizar un análisis estratificado para determinar si la modificación de efectos está presente en los datos
En el capítulo anterior, discutimos la confusión. Un factor de confusión, como recordarán, es una tercera variable que, si no se controla adecuadamente, conduce a una estimación sesgada de la asociación. La modificación del efecto también implica una tercera variable (no la exposición ni el resultado), pero en este caso, no queremos controlarla en absoluto. Más bien, la presencia de modificación de efectos es en sí misma un hallazgo interesante, y lo destacamos.
Cuando la modificación del efecto (también llamada interacción) está presente, habrá resultados diferentes para diferentes niveles de la tercera variable (también llamada covariable). Por ejemplo, si hacemos un estudio de cohorte sobre la cantidad de sueño y el promedio de calificaciones entre los estudiantes de la Universidad Estatal de Oregón (OSU) en el transcurso de un trimestre, podríamos recopilar estos datos:
| GPA | |||
| < 3.0 | ≥ 3.0 | ||
| Cantidad de sueño | < 8 horas | 25 | 25 |
| > 8 horas | 25 | 25 | |
Dado que se trataba de un estudio de cohorte, calculamos la razón de riesgo (RR):
No hay asociación entre la cantidad de sueño y el GPA posterior. Usando la frase de la plantilla, esto se puede afirmar:
Esta es una relación de riesgo de un estudio de cohorte, por lo que necesitamos incluir el marco de tiempo, lo que hice diciendo «para terminar el término». En cuanto a la confusión, nos referimos a esto como el RR sin ajustar o crudo.
Sin embargo, al hablar con los estudiantes, nos preguntamos si el género podría ser o no una covariable importante. Al igual que con la confusión, llevaríamos a cabo un análisis estratificado para verificar la modificación del efecto. Nuevamente, dibujamos tablas de 2 × 2 con la misma exposición (sueño) y resultado (GPA), pero dibujamos tablas separadas para hombres y mujeres (el género es la covariable). Hacemos esto mirando hacia atrás a los datos en bruto y averiguando cuántas de las 25 personas en la celda A (E+, D+) de arriba eran hombres y cuántas eran mujeres. Supongamos que de las 25 personas que reportaron < 8 horas y tuvieron un GPA < 3.0, 11 eran hombres y 14 mujeres. Luego dividimos de manera similar a los participantes de las células B, C y D, y hacemos tablas 2 x 2 específicas de estrato:
| Hombres | GPA | ||
| < 3.0 | ≥ 3.0 | ||
| Cantidad de horas de Sueño | < 8 horas | 11 | 14 |
| 8+ horas | 17 | 9 | |
| las Mujeres | GPA | ||
| < 3.0 | ≥ 3.0 | ||
| Cantidad de sueño | < 8 horas | 14 | 11 |
| 8+ horas | 8 | 16 | |
RRmen = \frac {(\frac{11}{25})}{(\frac{17}{26})} = 0.68
RRwomen = \frac {(\frac{14}{25})}{(\frac{8}{24})} = 1.7
Interpretaciones:
Entre los estudiantes del sexo masculino, los que dormían menos de 8 horas por noche tenían 0,68 veces el riesgo de tener un GPA < 3.0 al final del término, en comparación con los que informaron de 8 horas o más.
Entre las estudiantes, las que dormían menos de 8 horas por noche tenían 1,7 veces el riesgo de tener un GPA < 3,0 al final del curso, en comparación con las que reportaron 8 o más horas.
Dormir menos de 8 horas se asocia, en estos datos hipotéticos, con un promedio más alto entre los estudiantes varones (el «resultado» es un promedio bajo, por lo que un RR menor a 1 indica que los individuos expuestos tienen menos probabilidades de tener un promedio bajo) pero con un promedio más bajo entre las estudiantes femeninas.
El género en este caso está actuando como un modificador del efecto: la asociación entre sueño y GPA varía según los estratos de la covariable. Puede detectar la modificación del efecto al hacer un análisis estratificado, dado lo siguiente:
- Las medidas de asociación específicas del estrato son diferentes entre sí
- El crudo cae entre ellas
Si tiene una modificación de efecto, el siguiente paso es informar las medidas específicas del estrato. No calculamos una medida ajustada (sería cercana a 1.0, similar al crudo); lo interesante aquí es que los hombres y las mujeres reaccionan al sueño de manera diferente. La modificación de efectos es algo que queremos resaltar en nuestros resultados, no algo que se deba ajustar.
A diferencia de la confusión, donde un cambio del 10% de crudo a ajustado es una definición aceptada para la confusión, no existe una definición estandarizada de cuán diferentes deben ser las medidas específicas del estrato para llamar a algo un modificador de efecto. El umbral probablemente debería ser más alto que el necesario para declarar algo como un factor de confusión, porque una vez que declaras algo como un modificador de efecto, posteriormente estás obligado a informar los resultados por separado para cada nivel de la covariable, algo que reduce tu energía a la mitad por lo menos. Por lo tanto, en epidemiología, rara vez vemos evidencia de modificación de efectos reportada en la literatura. En pocas palabras,» diferente «suficiente para la modificación del efecto es» inequívocamente diferente.»
Al leer artículos, la modificación de efectos a veces se denomina interacción, o los autores pueden decir simplemente que están reportando análisis estratificados. Cualquiera de estas 3 frases es una pista de que hay una variable que actúa como modificador de efectos.
Ejemplo de modificación de efectos II
Tras la recesión impulsada por la burbuja inmobiliaria de 2008 (esta es la exposición), la economía estadounidense perdió muchos empleos. Aquí hay un gráfico que muestra el número de personas que estaban trabajando (el resultado) antes, durante y después de la recesión. Los resultados se presentan estratificados por género (una covariable), lo que significa que el analista sospechó que el género podría estar actuando como un modificador del efecto. De hecho, los resultados son ligeramente diferentes: los hombres (en azul) perdieron una mayor proporción de puestos de trabajo, y en 2014 aún no se habían recuperado a los niveles anteriores a la recesión, mientras que las mujeres (en rojo) perdieron menos puestos de trabajo y en 2014 se habían recuperado completamente.

Fuente: https://fred.stlouisfed.org/graph/fredgraph.png?g=qUs
¿Y si también estratificamos por edad? En primer lugar, aquí hay un gráfico que muestra cómo la recesión afectó los empleos de las personas de 55 años o más:
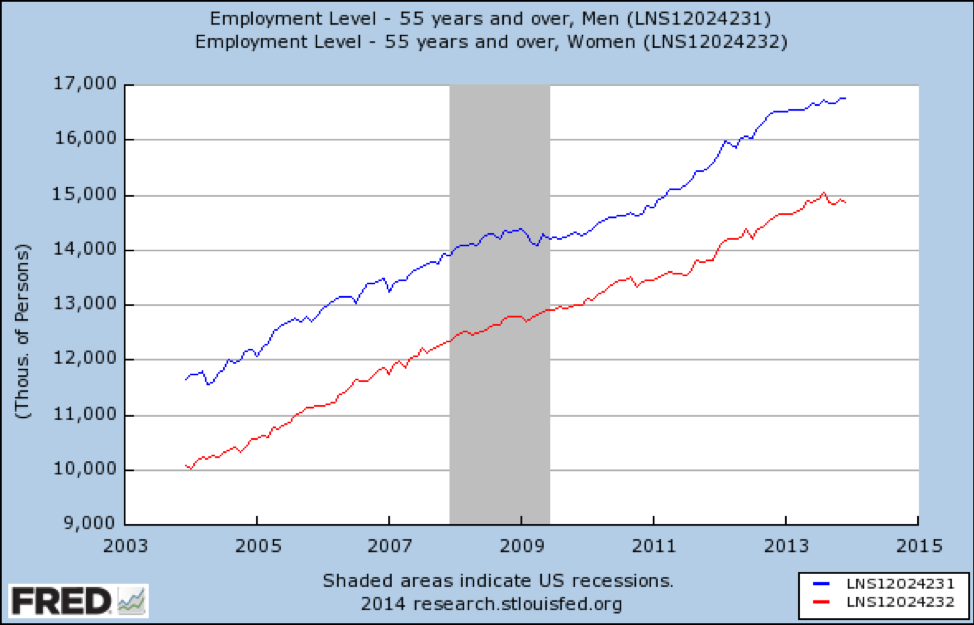
Fuente: https://fred.stlouisfed.org/graph/fredgraph.png?g=qUt
La recesión no afectó en absoluto a los trabajadores estadounidenses mayores. Tampoco estamos viendo la modificación del efecto por género-las 2 líneas son casi paralelas.
¿Qué pasa con los adultos jóvenes?
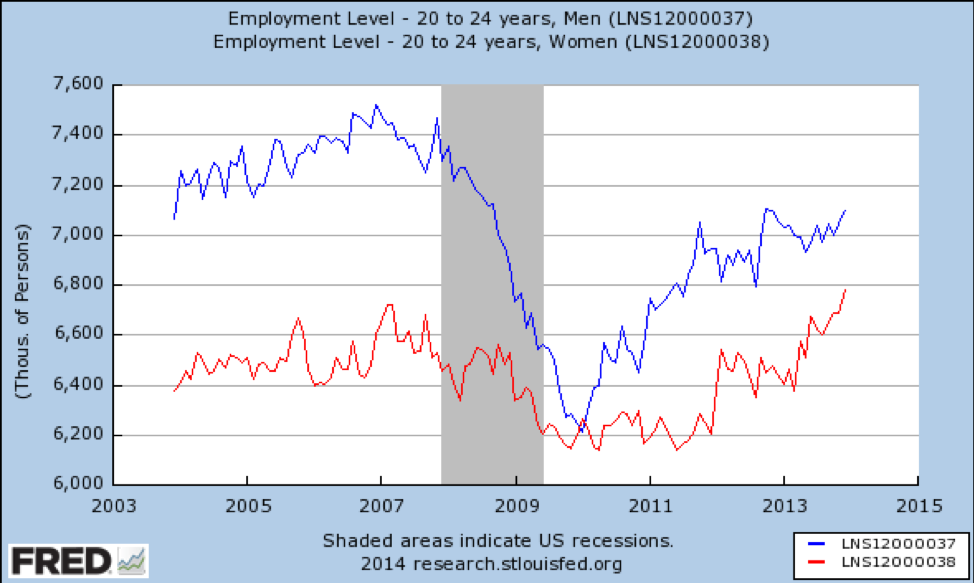
Fuente: https://fred.stlouisfed.org/graph/fredgraph.png?g=qUv
Aquí tenemos una importante modificación de los efectos por género: los hombres jóvenes perdieron una gran proporción de los empleos disponibles y no se habían recuperado completamente en 2014. Esto no es sorprendente, ya que la recesión fue causada en gran medida por la burbuja inmobiliaria, y los trabajadores de la construcción son en su mayoría hombres jóvenes. En cambio, las mujeres jóvenes perdieron una pequeña proporción de puestos de trabajo y se recuperaron rápidamente a niveles superiores a los previos a la profesión.
Finalmente, analizamos los empleos para jóvenes de 25 a 54 años:
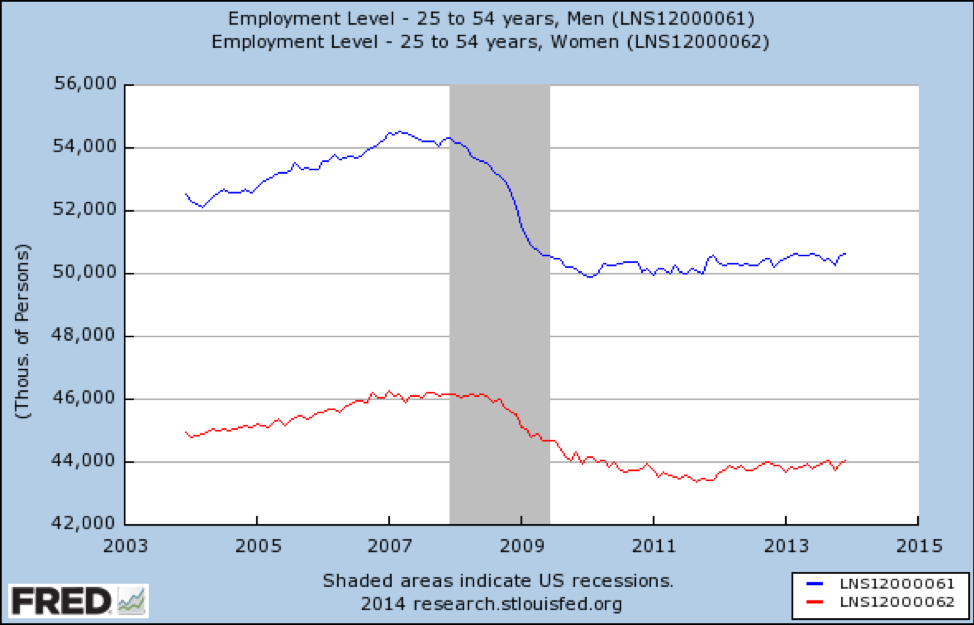
Fuente: https://fred.stlouisfed.org/graph/?id=LNS12000061
Aquí vemos una imagen muy sombría. En este grupo de edad, se perdieron empleos, más para los hombres que para las mujeres, y a partir de 2014 no se habían recuperado en absoluto.
Así, al examinar la respuesta del mercado de trabajo a la recesión de 2008, observamos una modificación sustancial de los efectos por edad (la recuperación de los puestos de trabajo varió drásticamente por edad) y, dentro de algunas categorías de edad, también algunas pruebas de modificación de los efectos por género. Los efectos de la recesión en el empleo fueron diferentes para las personas de diferentes edades y géneros.
Esto es importante porque las implicaciones políticas serían muy diferentes. Imagínese que estuviera trabajando como parte del gobierno federal y tratando de diseñar un paquete de estímulo económico o recuperación. Si los únicos datos que se hubieran obtenido procedieran del primer gráfico, sin los desgloses por edades, las posibles soluciones de política serían muy diferentes de si también se tuviera acceso al análisis estratificado por edades.
Con la confusión, al principio recibes la respuesta incorrecta porque la confusión no se distribuye de manera uniforme entre tus grupos. Esto distorsiona la medida de asociación que usted calcula (recuerde: tener pies más grandes se asocia con la velocidad de lectura solo debido a la confusión por nivel de grado). Así que en lugar de eso, necesitas recalcular la medida de asociación, esta vez ajustando para el confundidor.
Con la modificación de efectos, también está obteniendo inicialmente la respuesta incorrecta, pero esta vez es porque su muestra contiene al menos 2 subgrupos en los que la asociación exposición/enfermedad es diferente. En este caso, debe separar permanentemente esos subgrupos e informar los resultados (que pueden o no confundirse con otras covariables) por separado para cada estrato: en este caso, los hombres que duermen menos tienen promedios de calificación más altos que los hombres que duermen más, pero, al mismo tiempo, las mujeres que duermen más tienen promedios de calificación más altos que las mujeres que duermen menos.
Aquí hay una tabla de resumen que indica el proceso para tratar con posibles factores de confusión y modificadores de efectos. Gran parte del proceso es el mismo, independientemente del tipo de covariable que tenga (en todos los casos, debe medir la covariable durante su estudio y medirla bien!). Las áreas de diferencia se muestran en rojo.
| Confusión | Modificación del efecto | |
| Antes de planificar un estudio | Piense en qué variables podrían actuar como factores de confusión en función de lo que sabe sobre el proceso de exposición/enfermedad en estudio. | Piense en qué variables podrían actuar como modificadores de efectos en función de lo que sabe sobre el proceso de exposición/enfermedad en estudio. |
| Durante un estudio | Recopilar datos sobre cualquier covariable potencial: ¡los análisis estratificados / ajustados no se pueden realizar sin datos sobre la covariable! | Recopilar datos sobre cualquier covariable potencial-no se pueden realizar análisis estratificados / ajustados sin datos sobre la covariable. |
| Análisis: Paso 1 | Calcular la medida bruta de asociación (ignorando la covariable). | Calcular la medida bruta de asociación (ignorando la covariable). |
| Análisis: Paso 2 | Calcular medidas de asociación específicas de estrato, de modo que cada nivel de la covariable tenga su propia tabla 2 x 2. | Calcular medidas de asociación específicas de estrato, de modo que cada nivel de la covariable tenga su propia tabla 2 x 2. |
| Análisis: Paso 3 | Si las medidas específicas del estrato son similares entre sí, y al menos un 10% diferentes del crudo (que no se encuentra entre ellos), entonces la covariable es un factor de confusión. | Si las medidas específicas del estrato son diferentes entre sí, y el crudo se encuentra entre ellas, entonces la covariable es un modificador del efecto. |
| Escribir Resultados | Reporta una medida de asociación ajustada que controla el confundidor. | Informe de las medidas de asociación específicas del estrato. |
Imagine que realiza un estudio transversal de la actividad física y la demencia en personas mayores y calcula una razón de probabilidades (OR) no ajustada de 2.0. Cree que el estado civil puede ser una covariable importante, por lo que estratifica por «actualmente casado» versus «no casado actualmente» (que incluye nunca casado, divorciado y viudo). El quirófano entre las personas actualmente casadas es de 3,1, y el quirófano entre las personas no casadas es de 3,24. En este caso, el estado civil está actuando como un factor de confusión, y reportaríamos el OR ajustado (que sería 3.18 aproximadamente).
Imagine que hacer un ensayo aleatorizado de una dieta Mediterránea para prevenir el parto prematuro en mujeres embarazadas. Haces el ensayo y calculas un RR de 0,90. Usted piensa que tal vez la paridad podría ser una covariable importante, por lo que realiza un análisis estratificado. Entre nulliparas, el RR es 0,60, y entre multiparas, el RR es 1,15. Estos son diferentes entre sí, y lo crudo se encuentra entre ellos. En este caso, la paridad actúa como un modificador de efectos, por lo que reportaría los 2 RRs específicos del estrato por separado.
Imagine que está haciendo un estudio de casos y controles de melanoma y uso previo de camas de bronceado. El OR crudo es de 3,5, pero quizás el género es una covariable importante. El análisis estratificado arroja una OR de 3,45 en los hombres y de 3,56 en las mujeres. En este caso, la covariable (género) no es un factor de confusión ni un modificador de efectos. Decimos que no es un factor de confusión porque (1) el crudo se encuentra entre las 2 estimaciones específicas del estrato, pero también (2) las estimaciones específicas del estrato no son más de un 10% diferentes del crudo. Decimos que no es un modificador de efectos porque, 3.45 y 3.56 no son tan diferentes—en ambos casos, hay un efecto sustancial (aproximadamente 3.5 veces más alto). Informaríamos de la estimación bruta de asociación, ya que no requiere ajuste ni estratificación para tener en cuenta los efectos del género.
Sí! Por lo general, vemos esto cuando la covariable en cuestión es una variable continua, dicotomizada con el fin de verificar la modificación del efecto. Por ejemplo, si pensamos que la edad podría ser un modificador del efecto, podríamos dividir nuestra muestra en» viejo «y» joven » para el análisis estratificado, por ejemplo, mayores de 50 frente a 50 o menores. En la medida en que los niños de 51 años no son como los de 70 años, podríamos pasar por alto algunos matices importantes en los resultados, posiblemente porque existe en los datos una modificación adicional del efecto con más categorías (lo que reduciría el poder a casi nada, si informáramos por separado sobre estratos adicionales) o confusión «residual» como se discutió en el capítulo anterior. Más detalles están más allá del alcance de este libro, pero sepa que la misma covariable puede actuar teóricamente como un confundidor y un modificador de efectos, pero que rara vez se ve esto en la práctica.
Conclusión
A diferencia de la confusión, de cuyos efectos queremos deshacernos en nuestro análisis, la modificación de efectos es un hallazgo interesante en sí mismo, y lo reportamos. Para verificar la modificación de los efectos, realice un análisis estratificado. Si las medidas de asociación específicas del estrato son diferentes entre sí y el crudo se encuentra entre ellas, entonces es probable que la variable en cuestión esté actuando como un modificador de efectos. Informe los resultados por separado para cada estrato de la covariable.
Una mesa final con todo junto:
| Si estos son sus ORs/Rr: | ||||
| Crudo/Sin corregir | Estrato | Estrato | Entonces la covariable es… | Y que le informe… |
| 2.0 | 1.0 | 3.2 | un efecto modificador | el 2 estrato específico de las medidas de asociación |
| 2.0 | 3.5 | 3.6 | un factor de confusión | una medición ajustada |
| 2.0 | 1.9 | 2.0 | nada interesante | la medida bruta |
Un error sistemático en un estudio (algunas personas lo llaman sesgo; yo prefiero no hacerlo) que es causado por una tercera variable que interfiere en la relación exposición-enfermedad.
Se refiere al escenario en el que la relación entre una exposición y un resultado varía en función de una tercera variable. Por ejemplo, tal vez el yoga previene las lesiones del LCA en las mujeres, pero no en los hombres. El sexo en ese escenario es el modificador del efecto. La modificación de efectos no es lo mismo que la confusión.
La probabilidad de que su estudio encuentre algo que esté ahí. Potencia = 1-β; beta es la tasa de error de tipo II. Los estudios pequeños, o estudios de eventos raros, suelen tener poca potencia.
Cuántos hijos ha tenido una mujer. Las mujeres nulíparas (también conocidas como nulíparas) aún no han tenido su primer hijo (pueden estar embarazadas, pero aún no lo han tenido), y las parias han tenido al menos un hijo anterior. Los multiparas han tenido al menos dos hijos anteriores; los primíparas han tenido un hijo anterior.
Este es el primer embarazo de una mujer.
Esta mujer ha tenido otros hijos.