KDnuggets

Por Sydney Firmin, Alteryx.

«Esencialmente, todos los modelos son incorrectos, pero algunos modelos son útiles.»- George Box

Esta famosa cita de George Box se registró por primera vez en 1976 en el artículo» Science and Statistics», publicado en el Journal of the American Statistical Association. Es una cita importante para el campo de la estadística y los modelos analíticos y se puede descomprimir en dos partes.

Todos los modelos son incorrectos

Para profundizar en esta declaración, necesitamos definir y examinar qué es un modelo.

Para el contexto de este artículo, un modelo puede considerarse como una representación simplificada de un sistema u objeto. Los modelos estadísticos aproximan patrones en un conjunto de datos haciendo suposiciones sobre los datos, así como sobre el entorno en el que se recopilaron y aplicaron.

Las tres grandes categorías de supuestos realizados por los modelos estadísticos son supuestos distributivos (supuestos sobre la distribución de valores en una variable o la distribución de errores de observación), supuestos estructurales (supuestos sobre la relación funcional entre variables) y supuestos de variación cruzada (distribución de probabilidad conjunta).

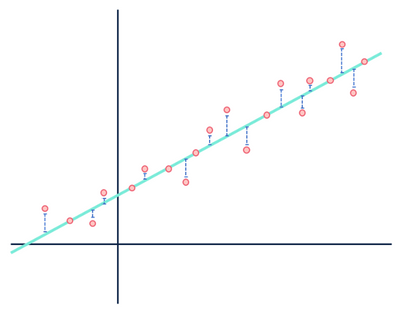
Por ejemplo, un modelo de regresión lineal asume que las relaciones entre variables en un conjunto de datos son lineales (y solo lineales). A los ojos de un modelo lineal, cualquier distancia entre las observaciones que componen el conjunto de datos y la línea modelada es solo ruido (es decir, fluctuaciones aleatorias o inexplicables en los datos) y, en última instancia, puede ignorarse.

Pagar ninguna mente a las distancias en azul.

George Box declaró que todos los modelos están equivocados específicamente en el contexto de los modelos estadísticos. Debido a que la naturaleza misma de un modelo es una representación simplificada e idealizada de algo, todos los modelos estarán equivocados en algún sentido. Los modelos nunca serán «la verdad» si la verdad significa completamente representativa de la realidad. Es muy importante tener en cuenta las suposiciones hechas al generar un modelo porque los modelos solo son verdaderamente útiles cuando las suposiciones se sostienen.

Mapas y miniaturas

Observaciones similares a «todos los modelos son incorrectos» de Box están presentes en muchos campos diferentes.

Hay un aforismo que hace referencia a la relación mapa-territorio, atribuido a Alfred Korzybski:

Un mapa no es el territorio que representa, pero, si es correcto, tiene una estructura similar al territorio, lo que explica su utilidad.

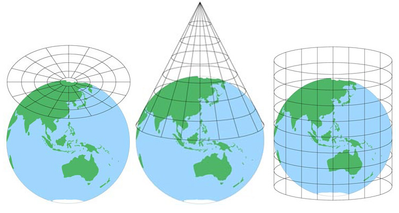
Los mapas son útiles porque son abstracciones de un objeto real a una escala más manejable, pero siempre excluirán algún nivel de detalle. Dependiendo de la cantidad de área que incluya un mapa, también puede haber cierta distorsión debido a la proyección del mapa (causada por el complicado proceso de convertir un globo esférico en una representación plana).

(fuente de la Imagen.)

El único mapa verdaderamente preciso sería una réplica 1:1 del territorio que representa. Sin embargo, un mapa como ese no sería más útil que navegar por el propio territorio.

Considere la cita del poeta Paul Valery:

Todo lo simple es falso. Todo lo que es complejo es inutilizable.

Nombrada en honor a un profesor de negocios de Stanford, la Paradoja de Bonini describe el desafío de crear modelos útiles y completos o simulaciones de sistemas complejos. A menudo hay un acto de equilibrio entre la complejidad y la precisión en el desarrollo de modelos. Si el objetivo de un modelo es hacer una relación o sistema más claro, la complejidad añadida anula ese propósito (aunque podría hacer que el modelo sea más preciso).

En un nivel alto, la relación mapa-territorio también describe la relación entre un objeto y una representación del objeto.

Si alguna vez has tomado una clase de filosofía, es posible que te hayas encontrado con la obra La traición de las imágenes del artista surrealista Rene Magritte.

El texto se traduce como » Esto no es una tubería.»Y no lo es. No podemos rellenar esta imagen (digital) con tabaco y fumarla, ya que es solo una representación de un objeto real.

Los modelos son abstracciones. Al igual que los mapas, los modelos arquitectónicos en miniatura o los esquemas, no pueden capturar cada detalle del objeto o sistema en el que se basan, aunque solo sea porque no existen en el mundo real y no funcionan de la misma manera.

Si Todos Los Modelos Están Equivocados, ¿Por Qué Molestarse?

El aforismo de George Box no está exento de críticas.

El problema que muchos estadísticos tienen con esta cita parece dividirse en dos categorías:

1. El hecho de que los modelos estén equivocados es una afirmación obvia. Por supuesto que todos los modelos están equivocados, son modelos.
2. Esta cita se utiliza como excusa para los malos modelos.

El estadístico J. Michael Steele ha sido crítico con el adagio (ver este ensayo personal). El argumento principal de Steele es que «incorrecto» solo entra en juego si el modelo no responde correctamente a la pregunta que afirma responder (p. ej., que un edificio en un mapa está mal etiquetado, no que el edificio esté representado por un pequeño cuadrado). Steele pasa al estado:

La mayoría de los métodos estadísticos publicados anhelan un ejemplo honesto.

Steele argumenta que los modelos estadísticos a menudo no están a la altura de una medida de aptitud adecuada, y muchos modelos desarrollados por estadísticos no son suficientes para sus casos de uso previstos.

En el artículo La estadística como Ciencia, No como Arte: La Manera de Sobrevivir en la Ciencia de Datos, Mark van der Laan (Estadística en UC Berkeley) atribuye la cita de la Caja como una causa que contribuye a los malos modelos estadísticos y la descarta como «una completa tontería.»Continúa escribiendo:

La base de las estadísticas (…) no podía haber sido seleccionar arbitrariamente un modelo estadístico «conveniente». Sin embargo, eso es precisamente lo que la mayoría de los estadísticos hacen alegremente, refiriéndose orgullosamente a la cita: «Todos los modelos están equivocados, pero algunos son útiles.»Debido a esto, los modelos que son tan poco realistas que están indexados por un parámetro de dimensión finita siguen siendo el status quo, a pesar de que todo el mundo está de acuerdo en que se sabe que son falsos.

Como solución, Van der Laan llama a los estadísticos para que dejen de usar la cita de Box y se comprometan a tomar en serio los datos, las estadísticas y el método científico. Hace un llamamiento a los estadísticos para que dediquen tiempo a aprender cómo se generaron los datos de un conjunto de datos determinado y se comprometan a desarrollar modelos estadísticos realistas utilizando el aprendizaje automático y técnicas de estimación adaptativas a los datos en lugar de modelos paramétricos más tradicionales.

Este artículo tiene respuestas de los estadísticos Michael Lavine y Christopher Tong, así como una respuesta a las respuestas del autor original. Los dos estadísticos refutantes señalan ejemplos en los que se sabe que los modelos son incorrectos, pero a menudo se emplean porque son útiles y adecuados para un problema determinado. Sus ejemplos incluyen los tres modelos diferentes de luz que se encuentran en el campo de la óptica (óptica geométrica, óptica física y óptica cuántica; los tres modelos representan la luz de manera diferente, son «incorrectos» en algún sentido y todavía se emplean hoy en día), y la relación (casi) lineal entre el registro de flujo de carbono y la temperatura del suelo que se encuentra en los datos recopilados en el Bosque de Harvard.

A su vez, Van der Laan responde a estos ejemplos y otras críticas de su artículo, específicamente a su concepto de encontrar un modelo «verdadero». Las cartas de respuesta definitivamente vale la pena leerlas si está interesado. Esto representa un área activa de debate en los campos de la estadística y la ciencia de datos.

Pero algunos modelos son Útiles

A pesar de las limitaciones de los modelos, muchos modelos pueden ser muy útiles. Debido a que son simplificados, los modelos a menudo son útiles para comprender un determinado componente o faceta de un sistema.

En el contexto de la ciencia de datos, el aprendizaje automático y los modelos estadísticos pueden ser útiles para estimar (predecir) valores desconocidos. En muchos contextos, si las suposiciones del modelo se mantienen, una estimación incierta proporcionada por un modelo estadístico sólido aún puede ser muy útil para tomar decisiones.

La segunda mitad menos citada de la sabiduría de George Box es esta:

«La pregunta práctica es qué tan erróneo debe ser el do (los modelos) para no ser útil.»- George Box

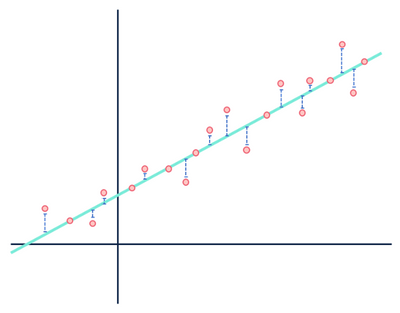
Echemos otro vistazo a nuestro ejemplo de regresión lineal:

En su mayoría, pasé demasiado tiempo en esta imagen para usarla solo una vez.

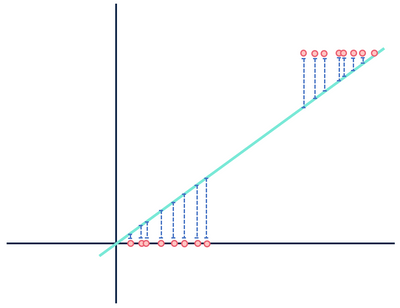
Ahora, echemos un vistazo a otro modelo teórico de regresión lineal que se ajusta a un conjunto de datos diferente.

Pagar ninguna mente a las distancias… espera, esto no puede ser correcto.

Ambas figuras muestran errores, pero un conjunto de datos muestra una relación claramente lineal mientras que el otro es logístico. Ambos modelos son «incorrectos», pero uno captura claramente una relación real entre variables, mientras que el otro no, haciendo que uno sea útil y otro inútil. Descartar las distancias en azul como ruido es razonable si los datos tienen una relación lineal, pero esta suposición se desmorona cuando la relación tiene una forma funcional diferente a la del modelo seleccionado.

Hacer buenos modelos

El hecho de que los modelos estén equivocados o limitados en el alcance de lo que representan puede parecer obvio para muchas personas que trabajan con modelos, pero desafortunadamente, muchas personas no se dan cuenta o piensan mucho en ello. Por eso creo que es importante tener en cuenta las palabras de George Box al desarrollar un modelo. No debe utilizarse como excusa para construir malos modelos.

Para leer más, Steele tiene algunas notas de clase geniales: ¿El Modelo tiene sentido? ¿y el Modelo Tiene Sentido? Parte II: Explotación de la suficiencia. Otro gran recurso es el documento ‘Todos los modelos están equivocados»: una introducción a la incertidumbre de los modelos de un taller de selección de modelos celebrado en 2011 en Groninga.

Otra lectura interesante es Cuando Todos los Modelos están Equivocados en Temas de Ciencia y Tecnología, que llama a las palabras de Box como un llamado a una transparencia más estricta en los modelos científicos y estadísticos.

Lo importante de todo esto es asegurarse de que comprende qué aspectos de sus datos son capturados por su modelo y qué aspectos no lo son. Es fundamental verificar sus suposiciones y puntos de partida. Como estadístico o científico de datos, es su responsabilidad producir modelos rigurosos y conocer sus limitaciones. Informe siempre su incertidumbre, así como el alcance de su modelo. Con eso en mente, podrá hacer modelos que, aunque posiblemente estén equivocados, sin duda pueden ser útiles.

Original. Publicado con permiso.

Bio: Geógrafo de formación y geek de los datos de corazón, Sydney cree firmemente que los datos y el conocimiento son más valiosos cuando se pueden comunicar y comprender claramente. En su puesto actual como Ingeniera de Contenido de Ciencia de Datos, pasa sus días haciendo lo que más le gusta: transformar el conocimiento técnico y la investigación en contenido atractivo, creativo y divertido para la Comunidad de Alteryx.

Relacionados:

• Los 3 Errores Más Grandes en el Aprendizaje de la Ciencia de Datos
• 3 Grandes Problemas con Big Data y Cómo Resolverlos
• Elegir entre Candidatos de Modelo