Un Círculo se divide uniformemente en seis triángulos iguales
Hola Marilynn,
Primero, te diré mis suposiciones sobre cómo se ve tu imagen:
- Cada triángulo tiene un vértice (esquina) en el centro del círculo
- Cada triángulo tiene esquinas en la circunferencia del círculo (por lo tanto, dos lados de cada triángulo son un radio)
- Los triángulos comparten lados (no hay huecos entre triángulos)
La imagen general se parece a una flor, cada triángulo es un pétalo.

El área desconocida es lo que queda alrededor del exterior del círculo, entre la circunferencia y el lado exterior de cada triángulo. Esta área desconocida se divide en seis secciones congruentes (iguales en todos los sentidos, como los triángulos son «iguales» en todos los sentidos, incluyendo el área, la longitud del lado y la longitud del arco). No está claro si quiere decir que el área de un arco es Pi (en realidad no se divide el Pastel, aunque se pronuncia igual), o si las seis secciones juntas son Pi. En lo que sigue, asumiré que una de las secciones exteriores tiene un área de Pi, de modo que el área de las seis secciones juntas es 6 veces Pi. Necesitamos encontrar el radio del círculo, llámelo r.
También usaré P para representar Pi(o aprox. 3.14). Ahora, hay mucha información que podemos adornar de los triángulos:
- Los ángulos en el centro son todos de 60 grados. Esto se debe a que los seis ángulos en el centro son todos iguales, y un círculo tiene 360 grados. Así que 360 dividido por 6.
- Cada triángulo es Isósceles. Esto se debe a que dos lados son iguales (los lados que son un radio).
- Cada triángulo, de hecho, es equilátero. Debido a que es iscoceles, los dos ángulos exteriores también son iguales. Pero hay 180 grados en un triángulo, 60 ya se utilizan en el ángulo central, dejando 180-60 = 120 grados para los ángulos exteriores. Pero, 120 dividido por 2 es 60 grados, por lo que los tres ángulos son iguales, por lo que es isósculos.
- Cada lado en cada triángulo es de longitud r. Esto es porque tenemos 6 triángulos equiláteros congruentes («iguales» en todos los sentidos), y porque dos lados de cada triángulo son un radio.
De la geometría de los triángulos, necesitamos hacer algo de álgebra. Debido a que conocemos un área, y necesitamos un radio, necesitamos una fórmula (o ecuación) para el radio en términos de área (en lo que sigue, tenga en cuenta el objetivo de una fórmula). El área del círculo es P * r2 (r2 significa r cuadrado, y * significa multiplicar) El área de las secciones sobrantes fuera de los triángulos, pero dentro del círculo (un área que ya no es 6*P), también se puede encontrar restando el área de los triángulos del área del círculo. Necesitamos encontrar un área de uno de los triángulos equiláteros.
Método 1 para calcular un área de un triángulo
El área de un triángulo es b * h / 2 Aquí es donde se necesita algo de trigonometría: Dibuja una línea desde un vértice a un lado opuesto que divide el lado opuesto por la mitad y está en ángulos rectos. Esto divide el triángulo equilátero en dos triángulos congruentes en ángulo recto, y el lado nuevo es la altura, llámalo h. Necesitamos encontrar h.
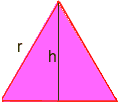
Usando trigonometría en uno de los triángulos en ángulo recto, tenemos sin60 = h / r Pero sin60 = sqr (3) / 2, donde sqr(3) significa la raíz cuadrada de tres, por lo que sqr(3)/2 = h/r multiplica ambos lados por r para obtener h = r*sqr(3)/2 r Ahora, el área de un triángulo equilátero es b*h/2 = (r) * (r * sqr(3)/2)/2 = (r2) * sqr(3)/4 r = sqr(6*P/(P-6*sqr (3)/4)) Utilice el orden de operaciones para calcular en una calculadora (con P=3.14): r= 5.896… Por lo tanto, el radio del círculo es de aprox. 5.9. Paul