Uso de Logaritmos en el Mundo Real

Los logaritmos están en todas partes. Nunca utilice las siguientes frases?

• 6 figuras
• Dígitos dobles
• Orden de magnitud
• Tasa de interés

Usted está describiendo números en términos de sus potencias de 10, un logaritmo. Y una tasa de interés es el logaritmo del crecimiento de una inversión.

¿Sorprendido de que los logaritmos sean tan comunes? Yo también. La mayoría de los intentos de Matemáticas en el Mundo Real (TM) señalan logaritmos en alguna fórmula arcana, o fingen que somos geólogos fascinados por la Escala de Richter. «A los científicos les importan los troncos, y tú también deberías. Además, ¿te imaginas un mundo sin zinc?»

No, No, No, no, no, no, no! (Mama mia!)

Math expresa conceptos con notación como «ln»o » log». Encontrar «matemáticas en el mundo real» significa encontrar ideas en la vida y ver cómo se podrían escribir con notación. ¡No busques los símbolos literales! ¿Cuándo fue la última vez que escribiste un signo de división? ¿Cuándo fue la última vez que cortaste algo de comida?

Ok, ok, lo entendemos: ¿ de qué se tratan los logaritmos?

Los logaritmos encuentran la causa de un efecto, es decir, la entrada para alguna salida

Un «efecto» común es ver crecer algo, como pasar de \1 100 a \1 150 en 5 años. ¿Cómo pasó esto? No estamos seguros, pero el logaritmo encuentra una posible causa: Un retorno continuo de ln (150/100) / 5 = 8.1% explicaría ese cambio. Puede que no sea la causa real (¿ocurrió todo el crecimiento en el último año?), pero es un promedio suave que podemos comparar con otros cambios.

Por cierto, la noción de «causa y efecto» está matizada. ¿Por qué 1000 es más grande que 100?

• 100 is 10, que creció por sí solo durante 2 períodos de tiempo($10 * 10$)
• 1000 is 10, que creció por sí solo durante 3 períodos de tiempo($10 * 10 * 10$)

Podemos pensar en números como salidas (1000 es «1000 salidas») e entradas («¿Cuántas veces necesita 10 crecer para hacer esas salidas?»). Así,

1000 outputs > 100 outputs

porque

3 inputs > 2 inputs

O en otras palabras:

log(1000) > log(100)

¿por Qué es útil?

Los logaritmos colocan los números en una escala amigable para los humanos.

Los grandes números nos rompen el cerebro. Millones y trillones son «realmente grandes» a pesar de que un millón de segundos son 12 días y un trillón de segundos son 30.000 años. Es la diferencia entre un año de vacaciones en Estados Unidos y la totalidad de la civilización humana.

El truco para superar la «gran ceguera numérica» es escribir números en términos de «entradas» (es decir, su base de poder 10). Esta escala más pequeña (de 0 a 100) es mucho más fácil de entender:

• poder de 0 = $10^0$ = 1 (de un solo elemento)
• poder de 1 = $10^1$ = 10
• el poder de 3 = $10^3$ = miles de
• potencia de 6 = $10^6$ = millones de
• potencia de 9 = $10^9$ = millones de
• alimentación de 12 = $10^12$ = billones
• potencia de 23 = $10^23$ = número de moléculas de una docena de gramos de carbono
• potencia del 80 = $10^80$ = número de moléculas en el universo

0 a 80 escala nos tomó de un solo elemento a la cantidad de cosas en el universo. No está mal.

Los logaritmos cuentan la multiplicación como pasos

Los logaritmos describen los cambios en términos de multiplicación: en los ejemplos anteriores, cada paso es 10 veces mayor. Con el logaritmo natural, cada paso es » e » (2.71828…) veces más.

Cuando se trata de una serie de multiplicaciones, los logaritmos ayudan a «contarlas», al igual que la suma cuenta para nosotros cuando se agregan efectos.

Muéstrame las matemáticas

Tiempo para la carne: ¡veamos dónde aparecen los logaritmos!

Salario de seis cifras o gasto de 2 dígitos

Estamos describiendo los números en términos de sus dígitos, p. ej. cuántos poderes de 10 tienen (están en las decenas, cientos, miles, diez miles, etc.).). Sumar un dígito significa «multiplicar por 10», i. e.

Los logaritmos cuentan el número de multiplicaciones agregadas, por lo que a partir de 1 (un solo dígito) agregamos 5 dígitos más (^10 ^ 5 5) y 100.000 obtienen un resultado de 6 cifras. Hablando de «6» en lugar de «cien mil» es la esencia de los logaritmos. Da una idea aproximada de la escala sin entrar en detalles.

Pregunta adicional: ¿Cómo describirías 500,000? Decir «6 cifras» es engañoso porque 6 cifras a menudo implica algo más cercano a 100,000. ¿Funcionaría «6,5 cifras»?

En realidad no. En nuestras cabezas, 6.5 significa «a mitad de camino» entre 6 y 7 cifras, pero esa es la mentalidad de una víbora. Con logaritmos a «.5 » significa la mitad en términos de multiplicación, es decir, la raíz cuadrada (^9^.5 means significa que la raíz cuadrada de 9 3 3 está a mitad de camino en términos de multiplicación porque es de 1 a 3 y de 3 a 9).

Tomando log (500,000) obtenemos 5.7, sumamos 1 para el dígito adicional, y podemos decir «500,000 es un 6.número de figura 7». Pruébalo aquí:

Orden de magnitud

A los geeks nos encanta esta frase. Significa aproximadamente «diferencia de 10 veces», pero suena más fresco que»1 dígito más grande».

En ordenadores, donde todo se cuenta con bits (1 o 0), cada bit tiene un efecto de duplicación (no 10x). Así que ir de 8 a 16 bits es «8 órdenes de magnitud» o 2 2^8 = 256 times veces más grande. («Más grande» en este caso se refiere a la cantidad de memoria que se puede abordar. Pasar de 16 a 32 bits significa un extra de 16 órdenes de magnitud, o 2 2^16 ~ ~ 65.536 veces más memoria que se puede abordar.

Tasas de interés

¿Cómo calculamos las tasas de crecimiento? Un país no tiene la intención de crecer al 8,56% anual. Observas el PIB un año y el PIB al siguiente, y tomas el logaritmo para encontrar la tasa de crecimiento implícita.

Mis dos interpretaciones favoritas del logaritmo natural (ln (x)), es decir, el logaritmo natural de 1.5:

• Suponiendo un crecimiento del 100%, ¿cuánto tiempo necesita crecer para llegar a 1,5? (.405, menos de la mitad del período de tiempo)
• Suponiendo 1 unidad de tiempo, ¿qué tan rápido necesita crecer para llegar a 1.5? (40.5% por año, compuesto continuamente)

Los logaritmos son la forma de averiguar qué tan rápido estamos creciendo.

Escala de medición: Google PageRank

Google otorga a cada página de la web una puntuación (PageRank) que es una medida aproximada de autoridad / importancia. Esta es una escala logarítmica, que en mi cabeza significa «PageRank cuenta el número de dígitos en su puntuación».

Por lo tanto, un sitio con pagerank 2 («2 dígitos») es 10 veces más popular que un sitio de PageRank 1. Mi sitio es PageRank 5 y CNN tiene PageRank 9, por lo que hay una diferencia de 4 órdenes de magnitud ($10^4$ = 10,000).

En términos generales, recibo alrededor de 7000 visitas / día. Usando mis matemáticas de sobre, puedo adivinar que CNN recibe alrededor de 7000 * 10,000 = 70 millones de visitas / día. (¿Cómo lo hice? En mi cabeza, creo que $7k * 10k = 70 * k * k = 70 * M$). Pueden tener un par de veces más que eso (100M, 200M), pero probablemente no hasta 700M.

Google transmite mucha información con una escala muy aproximada (1-10).

Escala de medición: Richter, Decibel, etc.

Suspiro. Estamos en el típico ejemplo de «logaritmos en el mundo real»: escala de Richter y Decibelios. La idea es poner los eventos que pueden variar drásticamente (terremotos) en una sola escala con un rango pequeño (típicamente de 1 a 10). Al igual que PageRank, cada aumento de 1 punto es una mejora de 10 veces en potencia. El terremoto más grande registrado por el hombre fue de 9,5; el impacto en la Península de Yucatán, que probablemente hizo que los dinosaurios se extinguieran, fue de 13.

Los decibelios son similares, aunque pueden ser negativos. Los sonidos pueden ir de intensamente silenciosos (pindrop) a extremadamente ruidosos (avión) y nuestro cerebro puede procesarlo todo. En realidad, el sonido del motor de un avión es millones (miles de millones, trillones) de veces más potente que una gota, y es inconveniente tener una escala que va de 1 a un tropeciento. Los registros mantienen todo a una escala razonable.

Gráficos logarítmicos

A menudo verá elementos trazados en una «escala logarítmica». En mi cabeza, esto significa que un lado está contando «número de dígitos» o «número de multiplicaciones», no el valor en sí. Una vez más, esto ayuda a mostrar eventos tremendamente variables en una sola escala (que van de 1 a 10, no de 1 a miles de millones).

La ley de Moore es un gran ejemplo: duplicamos el número de transistores cada 18 meses (imagen cortesía de Wikipedia).

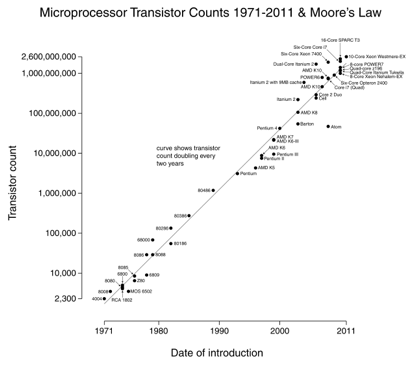
Lo bueno de los gráficos de escala logarítmica es que los cambios exponenciales (velocidad del procesador) aparecen como una línea recta. Crecer 10 veces al año significa que estás avanzando constantemente en la escala de «dígitos».

Hacia adelante y hacia arriba

Si un concepto es bien conocido pero no muy querido, significa que necesitamos construir nuestra intuición. Encuentre las analogías que funcionan, y no se conforme con la bazofia que un libro de texto sacará a relucir. En mi cabeza:

• Los logaritmos encuentran la causa raíz de un efecto (ver crecimiento, encontrar tasa de interés)
• Ayudan a contar multiplicaciones o dígitos, con la bonificación de recuentos parciales (500k es un número de 6,7 dígitos)

Matemáticas felices.

Otros Artículos De Esta Serie

1. Una Guía Intuitiva De Funciones Exponenciales & e
2. Desmitificar el Logaritmo Natural (ln)
3. Una Guía Visual de Tasas de Interés Simples, Compuestas y Continuas
4. Definiciones Comunes de e (Coloreado)
5. Entendiendo exponentes (¿Por qué 0^0 = 1?)
6. Usando Logaritmos en el Mundo Real
7. Cómo Pensar Con Exponentes Y Logaritmos
8. Entendiendo el Crecimiento Discreto vs. Continuo
9. ¿Qué significa realmente un exponente?
10. P: ¿Por qué e es especial? (2.718…, ¿no 2, 3,7 u otro número?)