Aurinkokunta: maa ja Kuu
planeetat ovat kymmenien ja satojen miljoonien kilometrien päässä meistä. Jotta näin suuria lukuja ei käytettäisi, astronominen yksikkö (AU) otetaan käyttöön etäisyyden yksikkönä, toisin sanoen maan ja auringon keskinäisen etäisyyden, 149 600 000 km.Valon matka kestää 8 minuuttia ja 19 sekuntia.
aurinkokunnan koko ylittää Pluton radan 40 AU: n etäisyydellä, ja se määritellään siten, että auringon vetovoima on yhtä suuri kuin meitä lähimpien tähtien vetovoima. Aurinkokunnan mitat olisivat tällöin luokkaa 1,5 105 AU. On selvää, että nämä ulottuvuudet ovat hyvin pieniä verrattuna galaksin tai näkyvän maailmankaikkeuden mittoihin. Näitä valtavia etäisyyksiä mittaavat yksiköt ovat valovuosi ja parsekki, joka vastaa 206 265 AU: ta tai 3,26 valovuotta.
aurinkokunnan planeetat jaetaan kahteen ryhmään: Merkuriuksen, Venuksen, maan ja Marsin muodostamaan maanpäälliseen ryhmään sekä Jupiterin, Saturnuksen, Uranuksen ja Neptunuksen muodostamaan jättiläisplaneettaryhmään.
kaikilla planeetoilla Venusta ja Merkuriusta lukuun ottamatta on satelliitteja, joista suurin osa kuuluu jättiläisplaneettoihin. Maapallolla, Jupiterilla, Saturnuksella ja Neptunuksella on suurimmat satelliitit: Kuu, Galilein löytämät Jupiterin satelliitit (Io, Europa, Ganymede, Callisto), Saturnuksen Titan-satelliitti ja Neptunuksen Triton.
asteroidit valtaavat laajan rengasmaisen alueen Marsin ja Jupiterin ratojen välissä, keskimäärin 2,75 AU: n etäisyydellä Auringosta. Suurin asteroidi on Ceres, jonka läpimitta on 1000 km.
komeetat, joita on luetteloitu noin 600, jaetaan kahteen ryhmään, lyhytjakso (alle 20 vuotta) ja pitkä jakso (yli 20 vuotta). Komeettojen alkuperästä on useita hypoteeseja, muun muassa hollantilaisen tähtitieteilijän J. Oortin.
planeettainvälisessä avaruudessa mainittujen kappaleiden lisäksi on suuri määrä erikokoisia, pääasiassa gramman tuhannes-tai miljoonasosan massaisia hiukkasia, joita kutsutaan meteoripölyksi. Näiden hiukkasten muodostuminen johtuu todennäköisesti suurempien kappaleiden (asteroidien) törmäyksistä ja niiden peräkkäisestä pirstoutumisesta koko aurinkokunnan olemassaolon ja evoluution ajan.
Meteoripöly aiheuttaa eläinradan valon ilmiön, joka havaitaan hämärän jälkeen tai ennen aamunkoittoa, koska nämä pölyhiukkaset hajottavat valoa. Suurin osa hiukkasista haihtuu päästessään maan ilmakehään (80-120 km: n korkeudessa) ja vain pieni osa pääsee maan pinnalle.
Katsotaanpa nyt joitakin aurinkokunnan planeettoihin
liittyviä tietoja ensin auringosta
| taivaankappale | Radio | massa |
|---|---|---|
| su | 6,96 * 108 m | 1,98 * 1030 kg |
sitten pois maasta
| taivaankappale | välieräakseli | jakso | massa |
|---|---|---|---|
| maa | 149,6 * 109 m | 1 vuosi=365,26 päivää | 5.98 * 1024 kg |
ja loput planeetat
| planeetta | semiduuriakseli (AU) | eksentrisyys | jakso (Vuodet) | massa |
|---|---|---|---|---|
| elohopea | 0.387 | 0.206 | 0.24 | 0.06 |
| Venus | 0.723 | 0.007 | 0.62 | 0.82 |
| maa | 1.000 | 0.017 | 1.00 | 1.00 |
| Mars | 1.524 | 0.093 | 1.88 | 0.11 |
| Jupiter | 5.203 | 0.048 | 11.86 | 318 |
| Saturnus | 9.539 | 0.056 | 29.46 | 95.1 |
| Uranus | 19.182 | 0.047 | 84.01 | 14.6 |
| Neptunus | 30.058 | 0.009 | 164.8 | 17.2 |
seuraavassa taulukossa annetaan lisätietoja:
- planeetan radan tason kaltevuus ekliptikan suhteen (Maan radan taso)
- pyörimisjakso akselinsa ympäri. Merkuriuksen ja Venuksen kaltaisilla planeetoilla tätä magnitudia on ollut hyvin vaikea mitata. Jupiterin, Saturnuksen, Uranuksen ja Neptunuksen kaasumaisilla kuorilla on differentiaalisen pyörimisen ominaisuus, eli niiden pyörähdysajat vaihtelevat leveysasteen mukaan.
- pyörimisakselin kaltevuus suhteessa radan tasoon. Venuksen tapauksessa se on 177º, mikä vastaa sitä, että akselin inklinaatio on 3º, mutta pyörimissuunta on käänteinen. Sama argumentti pätee Uranukseen, jonka mukaan Uranuksen pyörimisakseli on lähes sen radan tasossa.
| planeetta | Radan inklinaatio | kiertoaika | tiheys g / cm3 | Radio ekvaattori (km) | akselin kallistus | Ei. satelliittien |
|---|---|---|---|---|---|---|
| Merkurius | 7.0 | 58d.6 | 5.44 | 2 439 | <30º | 0 |
| Venus | 3.4 | 243d | 5.24 | 6 051 | 177 ° | 0 |
| maa | 0 | 23h.9 | 5.52 | 6 378 | 23.5 | 1 |
| Mars | 1. 8 | 24h.6 | 3.95 | 3 394 | 25.2 | 2 |
| Jupiter | 1.3 | 9h.9 | 1.33 | 71 398 | 3.1 | 16 |
| Saturn | 2.5 | 10 H.2 | 0.69 | 60 000 | 26.4 | 17 |
| Uranus | 0º.8 | 10 h.8 | 1.26 | 25 400 | 98º | 5 |
| Neptunus | 1. 8 | 15 h.8 | 1.67 | 24 750 | 29º | 2 |
satelliitit
lopuksi esitetään joitakin tietoja planeettojen suurista satelliiteista. Jupiterilla ja Saturnuksella on monia satelliitteja, jotka ovat paljon suurempia kuin Marsissa, mutta mainitsemme vain ne, jotka ovat kooltaan samanlaisia tai suurempia kuin meidän kuumme.
| planeetta | satelliitit | tiheys g/cm3 | keskimääräinen säde (km) | Radiorata (103 km) | jakso (päiviä) |
|---|---|---|---|---|---|
| maa | Kuu | 3.33 | 1 738 | 384.4 | 27.32 |
| Mars | Phobos | 2.1 | 13.5 | 9.38 | 0.319 |
| Deimos | 2.1 | 7.5 | 23.46 | 1.262 | |
| Jupiter | Io | 3.53 | 1 820 | 421.6 | 1.769 |
| Eurooppa | 3.03 | 1 565 | 670.9 | 3.551 | |
| Ganymede | 1.93 | 2 638 | 1 070 | 7.155 | |
| Calisto | 1.83 | 2 410 | 1 880 | 16.689 | |
| Saturnus | Titan | 1.9 | 2 575 | 1 221.9 | 15.95 |
| Neptunus | Newt | 2 200 | 394.7 | 5.84 |
toiminta
- määrittää Jupiter-planeetan massan radiotiedoista ja yhden sen satelliitin vallankumouskaudesta.
- määrittää Jupiter-planeetan satelliitin kiertoradan säde kyseisen planeetan massasta ja satelliitin vallankumouskausi.
- määrittää gravitaatiokentän g voimakkuuden planeettojen ja joidenkin satelliittien pinnalla niiden massan M ja säteen R tai tiheyden ρ ja säteen perusteella.
esimerkki: määritetään Jupiterin planeetan massa tietäen, että Io: n kiertoradan säde on 421 600 km ja että sen kierrosaika on 1 769 päivää. Fakta: vakio G on 6,67 * 10-11 Nm2 / kg2
esimerkki: Laske säde kiertoradalla satelliitin Callisto tietäen, että sen vallankumouskausi on 16.689 päivää ja massa planeetta Jupiter on 1.901·1027 kg. Tieto: vakio G on 6,67 * 10-11 Nm2/kg2
G = G M R 2 = 4π 3 GpR
tiedot: Vakio G on 6.67 * 10-11 nm2 / kg2
Kuu
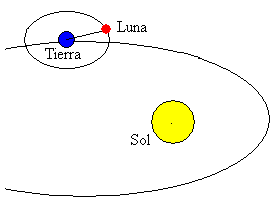
Kuu on yksi aurinkokunnan suurimmista kappaleista. Sen kiertorata on lähes pyöreä (eksentrisyys ε=0,05) ja sen radan taso on kallellaan 5º suhteessa Maan radan tasoon.
keskimääräinen etäisyys Maan keskipisteen ja kuun välillä on 384 400 km.Sen kiertoaika maapallon ympäri on 27 322 päivää. Kuun aseman muuttuminen suhteessa Aurinkoon synnyttää Kuun vaiheet.
Kuu esittää aina samat kasvot maan havaitsijalle maan Kuuhun kohdistamien vuorovesivoimien vaikutuksesta. Se tarkoittaa, että kuun pyörähdysaika akselinsa ympäri osuu aikaan, joka kuluu maata kiertävän radan suorittamiseen.
Kuu on taivaankappale, joka on kiehtonut eniten ihmislajia. Entinen Neuvostoliitto lähetti ensimmäisen kerran automaattilaivan, joka laskeutui Kuun pinnalle vuonna 1959. 20. heinäkuuta 1969 Neil Armstrong mukana Edwin Aldrin olivat ensimmäisinä miehet kävellä Kuun pinnalla osana Apollo 11 tehtävää. Viimeinen vierailu American astronautit Kuuhun tapahtui vuonna 1972.
alkuperä Kuu näyttää epävarmalta, on olemassa useita teorioita:
-
se muodostui samaan aikaan maan kanssa materiaalia sumu
-
taivaankappale on jaettu kahteen osaan, jolloin syntyy maa ja Kuu
-
että Kuu muodostui muualla ja vangittiin maa
-
että maa törmäsi suurikokoiseen (suunnilleen Marsin kokoiseen tai suurempaan) taivaankappaleeseen, ja että Kuu muodostui tämän törmäyksen karkottamasta aineksesta.
jälkimmäinen teoria vaikuttaa tällä hetkellä tiedeyhteisön eniten hyväksymältä.
Kuun polku
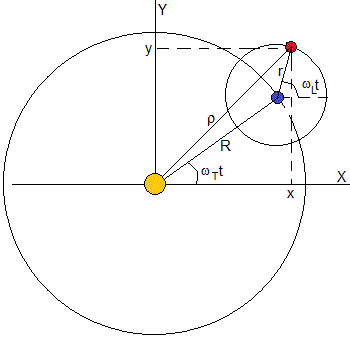
Ajatellaanpa planeettaa ja sen satelliittia. Planeetta kuvaa tähteään kiertävää pyöreää rataa, jonka säde on R ja jonka kulmanopeus wT=2π / PT on jakso tai aika, joka johtaa täydelliseen kääntymiseen. Satelliitti kuvaa ympyrän muotoista kiertorataa, jonka säde on R ja jonka kulmanopeus wL=2π/PL on PL jakso tai aika, joka kuluu täydellisen kierroksen tekemiseen
satelliitin sijainti suhteessa vertailujärjestelmään, jonka alkuperä on tähti, on
x=Rcos( ω T )+rcos( ω L t ) y=Risiko( ω T )+risiko( ω l t )
on α=WT/WL
{ X=RCOS( α ω l t )+rcos( ω l t ) y=risiko( α ω l t )+Risiko( ω L T ) { x=rcos( α 2π p l t )+rcos( 2π P L T ) Y=Risiko( α 2π P L T )+risiko( 2π p L T )
kutsumme τ=t/pl
x R =cos (α * 2πτ) + r R cos( 2πτ) ja R =sin( α·2πτ) + r R sin (2πτ)
edustamme satelliitin lentorataa α=0,1 ja suhdeluvun kolmea arvoa R/R.
- r/R<α. Esimerkki: r/R=0, 05
- r / R=α. Esimerkki: r/R=0, 1
- r / R >α. Esimerkki, r / R=0.15
alfa=0.1;r=0.15;fplot(@(t) r*cos(2*pi*t)+cos(2*pi*alfa*t), @(t) r*sin(2*pi*t)+sin(2*pi*alfa*t),)text(0.1,0.1,sprintf('\alpha=%1.2f',alfa))text(0.1,0.2,sprintf('r/R=%1.2f',r))axis equalgrid onxlabel('x/R')ylabel('y/R')title('Trayectoria de un satélite')
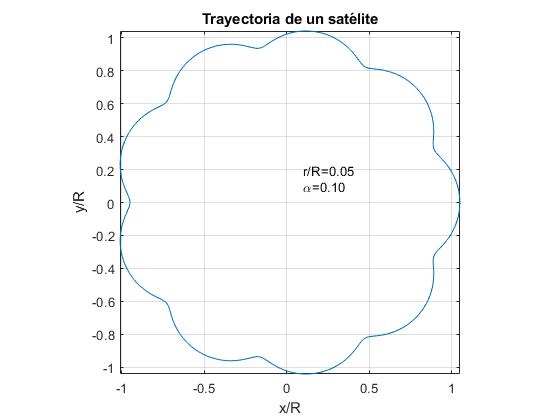
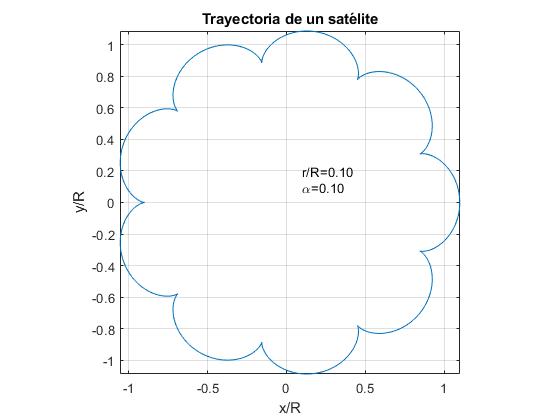
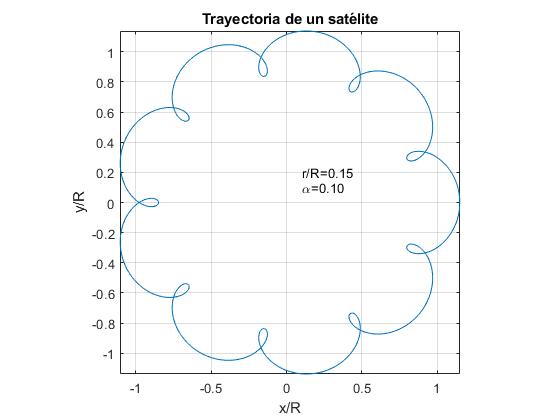
maan ja kuun osalta tiedot ovat:
- säde Kuun kiertoradalla: r=384,4 * 106 m, periodi PL = 27,32 d
- säde Maan kiertoradalla: R = 149, 6·109 m, jakso PT = 365, 26 d
α=wT/wL=PL/PT=0, 0748. r / R=0,0026
kuun kiertorata muistuttaa ensimmäistä lukua. Kuun liikeradan graafisessa esityksessä näille arvoille α ja r/R ei arvosta auringon ja kuun välisen säteittäisen etäisyyden heilahtelua
Kuun kiihtyvyys
etäisyys ρ auringosta Kuuhun on
ρ 2 = x 2 + y 2 = R 2 + r 2 +2rrcos( ( ω L − ω T )t )
laskemme kiihtyvyyden suorakulmaiset komponentit
{ DX DT =− ω t Risiko( ω T )− ω l Risiko( ω L T ) Dy DT = ω T Rcos( ω T )+ ω l rcos( ω L T ) { A x = d 2 x D T 2 =− ω T 2 rcos( ω t )− ω L 2 rcos( ω l t ) y = d 2 y D t 2 =− ω T 2 Risiko( ω T )− ω L 2 risiko( ω L t )
kiihtyvyyden säteittäinen komponentti
ρ = A → · ρ → ρ = A x x+ A y x 2 + y 2 =− ω T 2 R 2 + (ω T 2 + ω L 2 )Rrcos( ( ω L − ω T )t ) R 2 + r 2 + 2 rr cos( ( ω l − ω T )T )
pienin ja suurin arvo saadaan, kun cos((WL-wt)T)=±1
a max =− ω T 2 R 2 + ω L 2 r 2 + (ω T 2 + ω L 2 )Rr R 2 + r 2 +2 rr =−( ω T 2 R+ ω L 2 r ) min =− ω T 2 R 2 + ω L 2 r – (ω T 2 + ω L 2 )Rr R 2 + r 2 -2 rr = – (ω T 2 R-ω L 2 r )
>> R=149.6e9; %Tierra>> r=384.4e3; %Luna>> wT=2*pi/(365*24*60*60) %velocidad angular TierrawT = 1.9924e-07>> wL=2*pi/(27.32*24*60*60) %velocidad angular TierrawL = 2.6619e-06>> aM=-(wT^2*R+wL^2*r)aM = -0.0059>> am=-(wT^2*R-wL^2*r)am = -0.0059
Kuu on Aurinkokunnan ainoa satelliitti, jonka säteiskomponentti kiihtyvyydestä on negatiivinen, sanotaan, että ”Kuu putoaa Aurinkoa kohti”,
kuun vaiheet
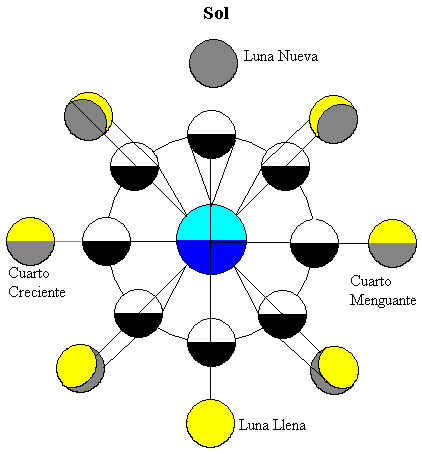
kuvassa Kuu on eri asennoissa Maata kiertävällä radallaan. Aurinko valaisee kaukana molemmat taivaankappaleet (kuvan yläosassa)
puolet kuusta on auringon valaisema (valkoisella värillä) ja puolet maata lähinnä olevasta Kuusta on maanpäällisen tarkkailijan nähtävissä. Kun kuu liikkuu maapallon ympäri, näemme auringon valaiseman osan eri osat (keltaiset alueet).
-
kun kuu on maan ja auringon välissä, maata lähinnä oleva Kuun osa on pimeä, joten kuuta ei voi nähdä, tätä vaihetta kutsutaan Uusikuuksi.
-
kun maa on auringon ja kuun välissä, maata lähinnä oleva Kuun osa on valaistu puolisko, tätä vaihetta kutsutaan täydeksi kuuksi.
-
kun kuu on väliasennoissa, vain puolet maan lähimmästä osasta valaistuu. Siksi näemme vain neljänneksen kuusta, näitä kahta vaihetta kutsutaan neljänneksiksi, jotka kasvavat tai vähenevät riippuen siitä, onko valaistu osa, joka näkyy maasta, pyrkii kasvamaan tai pienentymään.
Huomautus: Tämä interaktiivinen ohjelma yrittää selittää kuun vaiheita, mutta se on uskollinen esitys Kuun kiertoradasta, joka muodostaa 5°: n kulman ekliptikan tason kanssa (Maan kiertorata Auringon ympäri) tai maan akselin suunnan, joka on noin 23º normaalin kanssa ekliptikan tasoon nähden.
Kuun poikki on piirretty punainen viiva, jotta lukija voi ymmärtää Kuun pyörähdysajan ja maan kiertoradan suorittamiseen kuluvan ajan yhteensattuman, minkä vuoksi kuulla on aina samat kasvot maahan nähden.
kuunpimennykset
kuunpimennykset tapahtuvat aina, kun kuu on täydessä vaiheessa ja kun Aurinko, Maa ja Kuu ovat suorassa linjassa. Silloin Kuu on maan tuottamassa varjossa, kuten kuvassa näkyy.
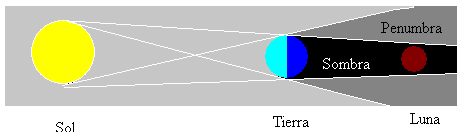
on muitakin kuunpimennystyyppejä, jotka riippuvat kolmen taivaankappaleen linjauksesta. Kuu voi olla valaisemattomalla alueella (varjo) tai osittain valaistulla alueella (penumbra).
auringonpimennys tapahtuu, kun Kuu seisoo auringon ja maan välissä, Kuu on uudessa vaiheessa. Kuu on 400 kertaa Aurinkoa pienempi, mutta kuu on 400 kertaa lähempänä maata, joten Maasta katsottuna molempien kappaleiden näennäinen koko on lähes sama. Kuu voi siis saada aikaan täydellisen auringonpimennyksen, jos se havaitaan Kuun Maahan heijastamalla varjovyöhykkeellä.
Kuutieto
| massa (kg) | 7.349·1022 |
| säde (km) | 1737. 4 |
| keskimääräinen tiheys (g/cm3) | 3.34 |
| keskimääräinen etäisyys maahan (km) | 384 000 |
| kiertorata (päivät) | 27.32166 |
| painovoiman kiihtyvyys päiväntasaajalla (m / s2) | 1.62 |
| radan eksentrisyys | 0.0549 |
| radan kaltevuus (astetta) | 5.1454 |
-
laske kuun kiertoradan säde maapallon ympäri tietäen, että jakso on 27,32 päivää. Laske myös kuun nopeus. Tiedot: G =6,67 * 10-11 Nm2 / kg2, maan massa on M=5,98 * 1024 kg.
-
laske painovoima g: n kiihtyvyys Kuun pinnalla.
-
laske osamäärä auringon halkaisijan ja kuun halkaisijan välillä. Laske keskimääräinen etäisyys auringon ja maan sekä kuun ja maan välillä. Tiedot: auringon säde 6,96 * 108 m, Keski-Maan-Auringon etäisyys 1,49·1011 m
-
laske Maa-Kuu-järjestelmän massakeskipisteen sijainti mitattuna maan keskipisteestä.
-
laske maan vetovoima kuussa, vertaa sitä auringon vetovoimaan kuussa. Päivämäärä: Auringon massa, 1,98 * 1030 kg
viitteet
M. Marov. Aurinkokunnan planeetat. Kustantamo Mir.
Lue lisää planeetoista kuinka monta planeettaa aurinkokunnassamme on?. ComofuncionaQue.com
jaksolle ”Kuun lentorata”
David C. Johnston. Sykloidiset polut fysiikassa translaatio-ja rotaatioliikkeiden superpositioina. On. J. Phys.87 (10), lokakuu 2019, s.808-810
Kuu kääntyy aina kohti aurinkoa. Matematiikkasivuja.