Bootstrap in R
Bootstrap on menetelmä, jolla voidaan päätellä populaatiosta otosaineistoja käyttäen.Bradley Efron esitteli sen ensimmäisen kerran thispaper-lehdessä vuonna 1979.Bootstrap perustuu näytteenottoon, joka vaihdetaan näytetiedoista. Thistechniquea voidaan käyttää minkä tahansa tilastotiedon keskivirheen estimointiin ja sille voidaan asettaa luottamusväli (Ci). Bootstrap on erityisen hyödyllinen, kun CI ei ole suljettu muoto, tai se on hyvin monimutkainen.
Oletetaan, että meillä on otos n:n alkuaineista: X = {x1, x2, …, xn} ja olemme kiinnostuneita CI: stä jonkin tilastollisen T = T(X). Bootstrapframework on yksinkertainen. Toistamme vain R kertaa seuraavan ohjelman: i-th toistoa, näyte korvaavia n elementtejä käytettävissä otoksesta (jotkut niistä poimitaan useammin kuin kerran). Soita thisnew sample i-th bootstrap näyte, Xi, ja calculatedesired statistic Ti = t (Xi).
tuloksena saadaan tilastomme R-arvot: T1, T2,…, TR. Kutsumme thembootstrap oivalluksia T tai bootstrap Jakelu T. sen perusteella voimme laskea CI T. on olemassa useita tapoja tehdä tämä. Prosenttipisteiden ottaminen tuntuu helpoimmalta.
Bootstrap toiminnassa
käytetään (jälleen kerran) tunnettua iris aineistoa. Tarkastelkaamme ensiriviä:
Oletetaan, että haluamme löytää CIs: n mediaanille Sepal.Length, mediaanilleSepal.Width ja Spearmanin sijoituskorrelaatiokertoimelle näiden kahden välillä. Käytämme R: n boot pakettia ja funktiota nimeltä… boot. Touse sen teho meidän täytyy luoda funktio, joka laskee ourstatistic (s) pois otetuista tiedoista. Sillä tulee olla vähintään kaksi parametria: a dataset ja vektori, joka sisältää indices tietojoukon alkuaineita, jotka poimittiin bootstrap-näytteen luomiseksi.
jos haluamme laskea CIs: n useammalle kuin yhdelle tilastolle kerralla, toimintomme on palautettava ne yhtenä vektorina.
meidän esimerkissämme se voi näyttää tältä:
library(boot)foo <- function(data, indices){ dt<-data c( cor(dt, dt, method='s'), median(dt), median(dt) )}foo valitsee halutut elementit (mitkä numerot tallennetaan indices) data: stä ja laskee korrelaatiokertoimen kahdesta ensimmäisestä sarakkeesta(method='s' valitaan Spearmanin rankingkerroin,method='p' tuloksena on Pearsonin kerroin) ja niiden mediaanit.
voimme myös lisätä joitakin ylimääräisiä argumentteja, esim. anna käyttäjän valita tyyppi odcorrelation kerroin:
foo <- function(data, indices, cor.type){ dt<-data c( cor(dt, dt, method=cor.type), median(dt), median(dt) )}jotta tämä opetusohjelma olisi yleisempi, käytänfoojälkimmäistä versiota.
nyt voidaan käyttää funktiota boot. Meidän on toimitettava sille nimi oddataset, juuri luomamme funktio, toistojen määrä (R)ja mahdolliset lisäargumentit funktiostamme (kuten cor.type). Alla käytetään set.seed tämän esimerkin toistettavuutta varten.
set.seed(12345)myBootstrap <- boot(iris, foo, R=1000, cor.type='s')boot funktio palauttaa kutsutun luokan objektin… (kyllä, olet oikeassa!)boot. Siinä on kaksi mielenkiintoista elementtiä. $t sisältää bootstrap-menettelyn (bootstrap realisations ofT) tuottamat statististen(s) arvojemme R-arvot):
$t0 sisältää arvot meidän tilasto(t) alkuperäinen, täydellinen, tietokokonaisuus:
myBootstrap$t0## -0.1667777 5.8000000 3.0000000tulostus boot konsolin objekti antaa lisätietoja:
original on sama kuin $t0. bias on ero Bootstrap-realisaatioiden keskiarvon ($t), jota kutsutaan bootstrap-estimaatiksi T: stä ja arvoksi alkuperäisessä aineistossa ($t0).
colMeans(myBootstrap$t)-myBootstrap$t0## 0.002546391 -0.013350000 0.007900000std. error on bootstrap-estimaatin keskivirhe, joka vastaa bootstrap-realisaatioiden standardipoikkeamaa.
apply(myBootstrap$t,2,sd)## 0.07573983 0.10295571 0.02726414erityyppiset bootstrap CIs
ennen kuin aloitamme CI: llä, on aina syytä tarkastella bootstrap-realisaatioiden jakautumista. Voimme käyttää plot funktiota, jossaindex kertoo, millä tilastoilla foo lasketut toivoisimme tolookia. Tässä index=1 on keihäsmiehen korrelaatiokerroin pituuden ja leveyden välillä, index=2 on mediaani od sepalpituus jaindex=3on mediaani od sepalleveys.
plot(myBootstrap, index=1)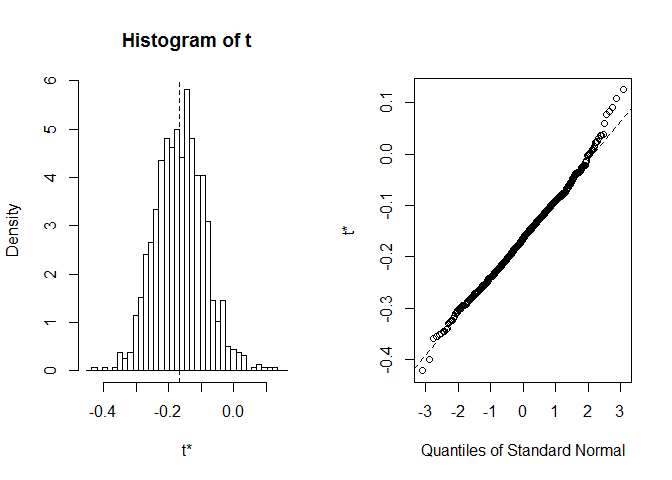
bootstrap-korrelaatiokertoimien jakautuminen vaikuttaa melko normaalilta. Etsitään vasikka. boot.ci. Sen oletusarvo on 95-prosenttinen CIs, mutta sitä voidaan muuttaa conf – parametrilla.
boot.ci sisältää 5 bootstrap-CIs-tyyppiä. Yksi niistä, studentizedinterval, on ainutlaatuinen. Se tarvitsee arvion bootstrap-varianssista. Wedidn ’ t provide it, so R prints a warning:bootstrap variances needed for studentized intervals. Varianceestimaatteja voi saada toisen tason bootstrapilla tai (helpompaa) jackknife-tekniikalla. Tämä on jotenkin soveltamisalan ulkopuolella tämän opetusohjelman, joten keskitytään loput neljä tyyppiä bootstrap CIs.
jos emme halua nähdä niitä kaikkia, voimme valita oleelliset type argumentista. Mahdolliset arvot ovat norm, basic, stud, perc, bca tai näiden vektori.
boot.ci funktio luo luokan objektin… (kyllä, olet arvannut!)bootci. Sen alkuaineita kutsutaan aivan kuten typeargumentissa käytettyjä CI-tyyppejä. $norm on 3-elementtinen vektori, joka sisältää luottamustason CI-rajoja.
boot.ci(myBootstrap, index=1, type='norm')$norm## conf ## 0.95 -0.3177714 -0.02087672$basic, $stud, $perc ja $bca ovat 5-elementtisiä vektoreita, jotka sisältävät myös PROSENTTIPISTEITÄ, joita käytetään CI: n laskemiseen (palaamme tähän myöhemmin):
boot.ci(myBootstrap, index=1, type='basic')$basic## conf ## 0.95 975.98 25.03 -0.3211981 -0.03285178hieman notaatio (Sori!)
saadaksemme käsityksen siitä, mitä eri CI-tyypit ovat, meidän on otettava käyttöön merkintä. Joten, anna:
- t⋆ on bootstrap − estimaatti (Bootstrap-estimaattien keskiarvo),
- t0 on tilastomme arvo alkuperäisessä aineistossa,
- se⋆ on bootstrap-estimaatin keskivirhe,
- B on Bootstrap-estimaatin biaseb = t⋆ – t0
- α be a confidence level, typically α = 0, 95,
- za be a $1 – \frac \alpha 2$ – Quantile of standardnormal distribution,
- θα be a α-persentiili of distribution of bootstraprealizations.
prosenttipisteen luottamusväli
, jossa on edellä oleva merkintä, prosenttipisteen luottamusväli on:
tämä vaatii vain asiaankuuluvia prosenttipisteitä. Ei muuta.
normaali luottamusväli
tyypillinen Wald-luottamusväli olisi:
bootstrap-tapauksessa se pitäisi korjata. Näin siitä tulee:
$$ t_0 – b \pm z_\alpha \cdot se^\star \\2t_0 – t^\star \pm z_\alpha \cdot se^\star$$
Basic CI
prosenttipiste CI: tä ei yleensä suositella, koska se toimii huonosti, kun se tulee outohäntäisiin jakeluihin. Basic CI (kutsutaan myös pivotal tai empiirinen CI) on paljon vankempi tähän. Tarkoituksena on laskea erot kunkin bootstrap-replikaation ja t0: n välillä ja käyttää niiden jakauman prosenttipisteitä. Fulldetails voidaan löytää esimerkiksi L. Wassermanin Allstatistiikasta
lopullinen kaava basic CI: lle on:
BCa CI
BCa tulee bias-corrected, accelerated. Kaava se ei ole kovin monimutkainen, mutta hieman unintuitive, joten jätän sen.KS. Thomas J. DiCiccio ja BradleyEfron, jos sinua kiinnostavat yksityiskohdat.
Metodin nimessä mainittu kiihtyvyys vaatii bootstrap-realisaatioiden spesifisten persentiilien käyttöä. Joskus voi käydä niin,että nämä olisivat joitakin äärimmäisiä prosenttipisteitä, mahdollisesti poikkeavia.BCa voi olla epävakaa tällaisissa tapauksissa.
katsotaan BCA CI: tä terälehden leveyden mediaaniksi. Alkuperäisissä tiedoissa tämä mediaani on täsmälleen 3.
saamme BCa CI: n (2, 9, 2, 9). Outoa, mutta onneksi Rvaroitti, että extreme order statistics used as endpoints. Katsotaan, mitä täällä tapahtui.:
plot(myBootstrap, index=3)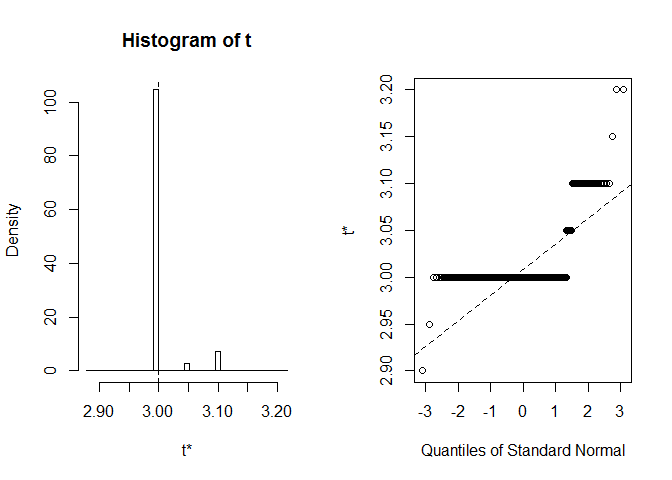
bootstrap-oivallusten levittäminen on epätavallista. Suurin osa heistä (yli 90%) on 3-vuotiaita.
table(myBootstrap$t)#### 2.9 2.95 3 3.05 3.1 3.15 3.2## 1 1 908 24 63 1 2tulosten replikointi
joskus on luotava bootstrap-replikaatioita. Jos siihen voidaan käyttää R, se ei ole ongelma. set.seed funktio ratkaisee ongelman.Bootstrap-replikaatioiden luominen muihin ohjelmistoihin olisi paljon monimutkaisempaa. Lisäksi suuren R: n kohdalla uudelleenlaskenta R ei myöskään voi olla vaihtoehto (esimerkiksi ajanpuutteen vuoksi).
voimme käsitellä tätä ongelmaa, säästämällä alkuaineiden indeksejä, jotka muodostivat jokaisen bootstrap-otoksen. Näin tekee boot.array funktio (jossa indices=T argumentti).
tableOfIndices<-boot.array(myBootstrap, indices=T)jokaisella rivillä on yksi bootstrap-näyte. Esim., ensimmäinen otos sisältää seuraavat elementit:
asetus indices=F (oletusarvo), saamme vastauksen kysymykseen ”Kuinka monta kertaa kukin alkuperäisen aineiston Elementti ilmestyi jokaisessa bootstrapsamplessa?”. Esimerkiksi ensimmäisessä näytteessä: 1. Elementti aineisto appearedonce, 2nd elementti ei näy lainkaan, 3rd Elementti ilmestyi kerran, 4thtwice ja niin edelleen.
tällainen taulukko mahdollistaa bootstrap-realisoinnin uudelleen Rulkopuolella.Tai R itse, kun emme halua käyttää set.seed ja tehdä kaikki thecomputation jälleen.
onceAgain<-apply(tableOfIndices, 1, foo, data=iris, cor.type='s')tarkistetaan, ovatko tulokset samat:
Kyllä ovat!
jos haluat oppia lisää koneoppimisesta R: ssä, osallistu Datacampin koneoppimisen Työkalupakkikurssille.