ero IIR-ja FIR-suodattimien välillä: käytännön suunnitteluopas

digitaalinen suodatin on matemaattinen algoritmi, joka toimii digitaalisella tietokokonaisuudella (esim.anturidata), jotta voidaan poimia kiinnostavia tietoja ja poistaa ei-toivottuja tietoja. Sovellukset tämäntyyppisen teknologian, sisältävät poistamalla glitches anturitiedot tai jopa puhdistaa melua mitattu signaali helpottaa tietojen analysointia. Mutta miten valita paras tyyppi digitaalisen suodattimen sovellukseemme? Entä mitä eroja on IIR-suodattimella ja FIR-suodattimella?

digitaaliset suodattimet jaetaan seuraaviin kahteen luokkaan:

• ääretön impulssivaste (IIR)
• äärellinen impulssivaste (FIR)

nimien mukaan kukin Suodatintyyppi luokitellaan sen impulssivasteen pituuden mukaan. Ennen yksityiskohtaisen matemaattisen analyysin aloittamista on kuitenkin järkevää arvostaa kunkin suodatintyypin suorituskyvyn ja ominaisuuksien eroja.

esimerkki

IIR: n ja FIR: n välisten erojen havainnollistamiseksi 14.kertaluvun FIR: n (kiinteä linja) ja 4. kertaluvun Chebyshev: N tyypin I IIR: n (katkonainen linja) taajuusvaste on esitetty alla kuvassa 1. Huomaa, että vaikka magnitudispektreillä on samanlainen vaimennus, IIR-suodattimen vaihespektri on epälineaarinen ohituskaistalla (\(\small 0\rightarrow7. 5Hz\)) ja muuttuu hyvin epälineaariseksi katkaisutaajuudella \(\small f_c=7.5 Hz\). Huomaa myös, että Kuutti vaatii suuremman määrän kertoimia (15 vs. IIR: n 10) vastaamaan IIR: n vaimennusominaisuuksia.

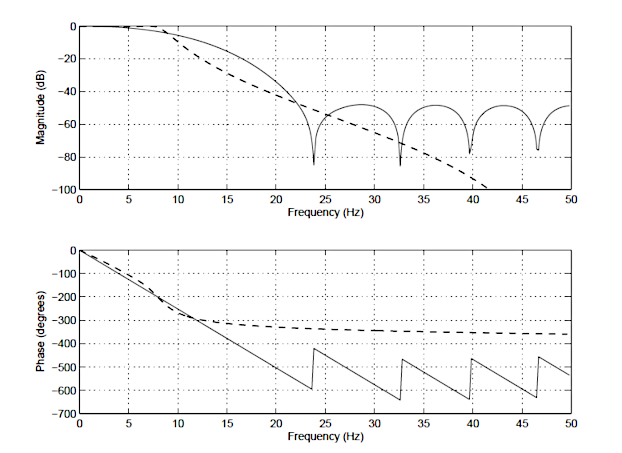
nämä ovat vain joitakin eroja kahden tyyppisiä suodattimia. Yksityiskohtainen yhteenveto kunkin suodatintyypin tärkeimmistä eduista ja haitoista seuraa nyt.

IIR-suodattimet

IIR-suodattimet (infinite impulse response) valitaan yleensä sovelluksiin, joissa lineaarinen vaihe ei ole liian tärkeä ja muisti on rajallinen. Niitä on käytetty laajalti äänen tasauksessa, biolääketieteellisessä anturisignaalin käsittelyssä, IoT/IIoT-älykkäissä antureissa ja nopeissa tietoliikenne/RF-sovelluksissa.

edut

• alhaiset toteutuskustannukset: vaatii vähemmän kertoimia ja muistia kuin FIR suodattimet täyttääkseen samanlaiset vaatimukset, eli katkaisutaajuus ja pysäytyskaistan vaimennus.
• alhainen latenssi: soveltuu reaaliaikaiseen ohjaukseen ja erittäin nopeisiin RF-sovelluksiin vähäisen kertoimien määrän vuoksi.
• analoginen ekvivalentti: voidaan käyttää analogisten suodattimien ominaisuuksien jäljittelemiseen käyttämällä S-z-tasokartoitusmuunnoksia.

haitat

• epälineaariset vaiheominaisuudet: IIR-suodattimen vaihekuviot ovat yleensä epälineaarisia, erityisesti lähellä katkaisutaajuuksia. All-pass tasaus suodattimia voidaan käyttää parantamaan passband vaihe ominaisuuksia.
• tarkempi analyysi: vaatii enemmän skaalausta ja numeerista ylivuotoanalyysiä, kun se toteutetaan kiinteässä pisteessä. Direct form II-suodatinrakenne on erityisen herkkä kvantisoinnin vaikutuksille ja vaatii erityistä huolellisuutta suunnitteluvaiheessa.
• numeerinen stabiilisuus: Vähemmän numeerisesti stabiili kuin niiden FIR (finite impulse response) kollegansa, johtuen takaisinkytkentäpoluista.

FIR-suodattimet

fir (finite impulse response) – suodattimet valitaan yleensä sovelluksiin, joissa lineaarinen vaihe on tärkeä ja käytettävissä on kohtuullinen määrä muistia ja laskennallista suorituskykyä. Niillä on laajalti käytössä audio-ja biolääketieteellisissä signaalinparannussovelluksissa. Niiden all-zero rakenne (käsitellään jäljempänä) varmistaa, että ne koskaan tullut epävakaa tahansa tulosignaalin, joka antaa heille selvä etu verrattuna IIR.

edut

• lineaarinen vaihe: kuuset voidaan helposti suunnitella siten, että niillä on lineaarinen vaihe. Tämä tarkoittaa sitä, että suodatettavaan signaaliin ei tule vaihevääristymää, koska kaikkia taajuuksia siirretään ajassa saman verran – näin niiden suhteelliset harmoniset suhteet (eli jatkuva ryhmä-ja vaiheviive) säilyvät. Tämä ei todellakaan pidä paikkaansa IIR-suodattimilla, joilla on epälineaarinen vaiheominaisuus.
• Stabiilisuus: EKT: t eivät käytä aikaisempia tuotosarvoja laskiessaan nykyistä tuotostaan, ts. heillä ei ole palautetta, he eivät voi koskaan tulla epävakaa tahansa tulosignaalin, joka on antaa heille selvä etu verrattuna IIR suodattimet.
• mielivaltainen taajuusvaste: Parks-McClellan ja ASN Filterscriptin firarb () – funktio mahdollistavat FIR: n suunnittelun mielivaltaisella magnitudivasteella. Tämä tarkoittaa, että kuusen voi räätälöidä helpommin kuin Iirin.
• kiinteän pisteen suorituskyky: kvantifioinnin vaikutukset ovat lievempiä kuin IIR: n vaikutukset.

haitat

• suuri laskenta – ja muistivaatimus: Kuuset vaativat yleensä paljon enemmän kertoimia terävän katkaisun saavuttamiseksi kuin IIR-kollegansa. Seurauksena tästä on, että ne vaativat paljon enemmän muistia ja huomattavasti suurempi määrä MAC (useita ja kerätä) toimintoja. Arm: n Cortex-M-ytimiin perustuvat nykyaikaiset mikrokontrolleriarkkitehtuurit sisältävät kuitenkin nyt DSP-laitteistotuen SIMD: n kautta (signal instruction, multiple data), joka nopeuttaa suodatustoimintaa merkittävästi.
• suurempi latenssi: suurempi määrä kertoimia, tarkoittaa, että yleensä FIR on vähemmän sopiva kuin IIR nopea suuren suoritustehon sovelluksia. Tämä on ongelmallista reaaliaikaisen suljetun silmukan ohjaus sovelluksia, joissa FIR suodatin voi olla liikaa ryhmä viive saavuttaa silmukan vakautta.
• ei analogista ekvivalenttia: Bilineaarisen, yhteensopivan z-muunnoksen (s-z-kartoitus) avulla analoginen suodatin voidaan helposti muuttaa vastaavaksi IIR-suodattimeksi. Tämä ei kuitenkaan ole mahdollista kuuselle, koska sillä ei ole analogista vastinetta.

matemaattiset määritelmät

kuten johdannossa on käsitelty, nimi IIR ja FIR ovat peräisin kunkin suodatintyypin matemaattisista määritelmistä, eli IIR-suodatin luokitellaan sen teoreettisesti äärettömän impulssivasteen mukaan,

\(\displaystyle
y (n)=\sum_{k = 0}^{\infty}h(k) x(n-k)
\)

ja FIR, joka luokitellaan sen äärellisen impulssivasteen perusteella,

analysoimme nyt kunkin suodatintyypin matemaattisia ominaisuuksia vuorollaan.

IIR-määritelmä

kuten edellä on esitetty, IIR-suodatin luokitellaan sen teoreettisesti äärettömän impulssivasteen perusteella,

\(\displaystyle y (n)=\sum_{k=0}^{\infty}h(k) x(n-k)\)

käytännössä IIR: n tulosta ei voida laskea tämän yhtälön avulla. Tämän vuoksi yhtälö voidaan kirjoittaa uudelleen äärellisen määrän napoja \(\small p\) ja nollia \(\small q\), jotka määritellään lineaarisen vakiokertoimen erotusyhtälön avulla:

\(\displaystyle
y(n)=\sum_{k=0}^{q}b_k x(n-k)-\sum_{k=1}^{p}a_ky (n-k)
\)

missä \(\small a_k\) ja \(\small b_k\) ovat suodattimen nimittäjän ja osoittajan polynomikertoimet, joiden juuret ovat yhtä suuret kuin suodattimen navat ja nollat. Näin erotusyhtälön ja z-muunnoksen (siirtofunktion) välinen suhde voidaan siis määritellä käyttämällä z-muunnoksen viiveominaisuutta siten, että,

\(\displaystyle
\sum_{k=0}^{q}b_kx(n-k)-\sum_{k=1}^{p}a_ky(n-k)\quad\stackrel{\displaystyle\mathcal{Z}}{\longleftrightarrow}\quad\frac{\sum\limits_{k=0}^q b_kz^{- k}}{1 + \sum\limits_{k=1}^p a_kz^{-k}}
\)

kuten nähdään, siirtofunktio on suodattimen taajuusalueen esitys. Huomaa myös, että pylväät toimivat lähtötiedoilla ja nollat syöttötiedoilla. Koska navat vaikuttavat lähtötietoihin ja vaikuttavat stabiiliuteen, on oleellista, että niiden säteet pysyvät yksikköympyrän sisällä (eli <1) bibon (rajattu tulo, rajattu lähtö) stabiilisuudessa. Nollien säteet ovat vähemmän kriittisiä, koska ne eivät vaikuta suodattimen stabiiliuteen. Tämä on ensisijainen syy, miksi all-zero FIR (finite impulse response) suodattimet ovat aina stabiileja.

BIBON stabiilisuus

lineaarisen aika-invariantin (lti) systeemin (kuten digitaalisen suodattimen) sanotaan olevan rajoittunut tulo, rajoittunut lähtö stabiili tai BIBO stabiili, jos jokainen rajoittunut tulo synnyttää rajoittuneen ulostulon, kuten

\(\displaystyle \sum_{k=0}^{\infty}\left|h(k)\right|<\infty \)

missä \(\small h(k)\) on lti-järjestelmän impulssivaste. Tätä yhtälöä analysoitaessa pitäisi olla selvää, että Bibo-stabiilisuuskriteeri täyttyy vain, jos systeemin navat ovat yksikköympyrän sisällä, koska systeemin Roc (konvergenssialueen) tulee sisältää yksikköympyrä. Näin ollen riittää sanoa, että rajattu tulosignaali tuottaa aina rajatun lähtösignaalin, jos kaikki napat ovat yksikön ympyrän sisällä.

tämä vaatimus ei rajoita nollia, minkä vuoksi ne voivat sijaita missä tahansa Z-tasossa, koska ne eivät suoraan vaikuta järjestelmän vakauteen. Siksi systeemin stabiilisuuden analyysi voidaan tehdä laskemalla ensin siirtofunktion juuret (eli osoittajan ja nimittäjän polynomien juuret) ja piirtämällä sitten vastaavat napat ja nollat Z-tason päälle.

mielenkiintoinen tilanne syntyy, jos yksikin Napa sijaitsee yksikköympyrällä, sillä systeemin sanotaan olevan marginaalisesti stabiili, koska se ei ole stabiili eikä epävakaa. Vaikka marginaalisesti vakaa järjestelmät eivät ole BIBO vakaa, ne ovat hyödyntäneet digitaalinen oskillaattori suunnittelijat, koska niiden impulssivaste tarjoaa yksinkertaisen menetelmän tuottaa siniaaltoja, jotka ovat osoittautuneet korvaamaton alalla televiestinnän.

Biquad IIR-suodattimet

tässä käsitellyn IIR-suodattimen toteutuksen sanotaan olevan biquad, koska siinä on kaksi napaa ja kaksi nollaa, kuten alla olevassa kuvassa 2 esitetään. Biquad-toteutus on erityisen hyödyllinen kiintopistetoteutuksissa, sillä kvantisoinnin ja numeerisen stabiilisuuden vaikutukset minimoidaan. Biquad-toteutuksen kokonaismenestys riippuu kuitenkin käytettävissä olevasta numerotarkkuudesta, jonka on oltava riittävän riittävä, jotta kvantifioidut napat ovat aina yksikköympyrän sisällä.

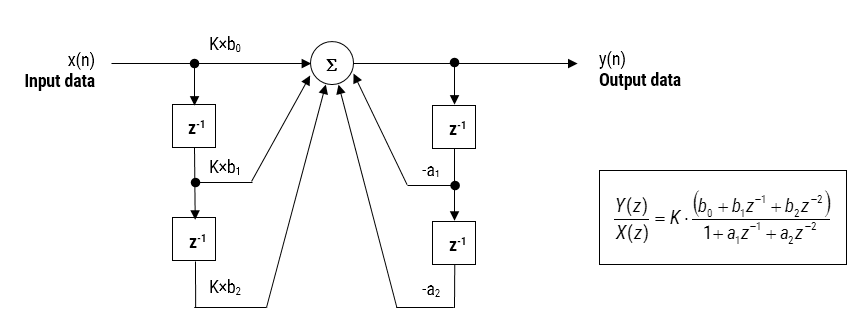
kuva 2: suora muoto I (biquad) IIR suodattimen toteutus ja siirtofunktio.

kuviota 2 analysoitaessa voidaan nähdä, että biquad-rakenne koostuu itse asiassa kahdesta takaisinkytkentäpolusta (skaalataan \(\small a_1\) ja \(\small a_2\)), kolmesta syöttöpolusta (skaalataan \(\small b_0, b_1\) ja \(\small b_2\)) sekä lohkovoitosta \(\small K\). Näin ollen kuvan 1 suodatusoperaatio voidaan tiivistää seuraavalla yksinkertaisella rekursiivisella yhtälöllä:

\(\displaystyle y (n)=k\times\Big-a_1 y(n-1) – a_2 y (n-2)\)

analysoimalla yhtälö, huomaa, että biquad toteutus vaatii vain neljä lisäyksiä (vaatii vain yhden kertymä) ja viisi multiplications, joka voidaan helposti sovittaa mihin tahansa Cortex-M Mikrokontrolleri. Lohkovoitto, \(\small K\) voidaan myös esikertoa eteenpäin-polkukertoimilla ennen toteutusta.

Biquad-suodattimien kokoelmaa kutsutaan Biquad-kaskadiksi, kuten alla on esitetty.

ASN suodatin suunnittelija voi suunnitella ja toteuttaa kaskadi jopa 50 biquads (Professional edition vain).

Liukulukurakenne

käytettäessä suodatinta liukulukurakenteessa (eli käyttämällä kahden tai yhden tarkkuuden aritmetiikkaa) suoria II-muotoja pidetään parempana vaihtoehtona kuin suoraa I-muotoa. Suoraa muotoa II Transponoitua rakennetta pidetään numeerisesti tarkimpana liukupisteen toteutuksessa, sillä numeerisen swampingin haittavaikutukset minimoidaan erotusyhtälöitä analysoimalla.

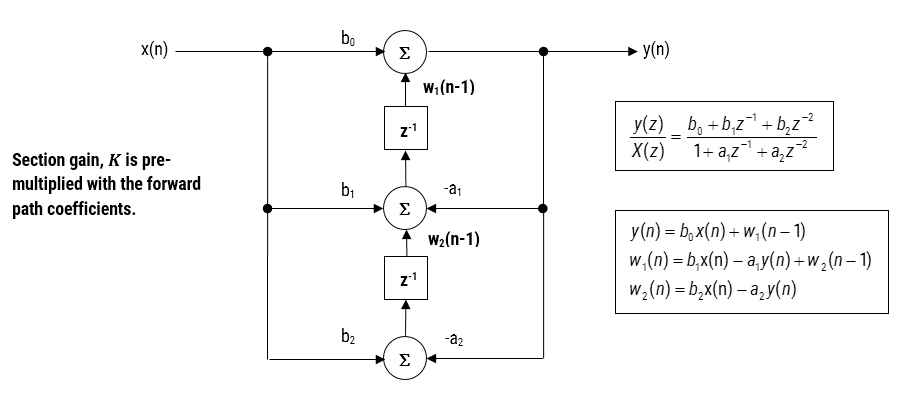
kuva 3-Direct Form II Transponed strutre, transfer function and difference equations

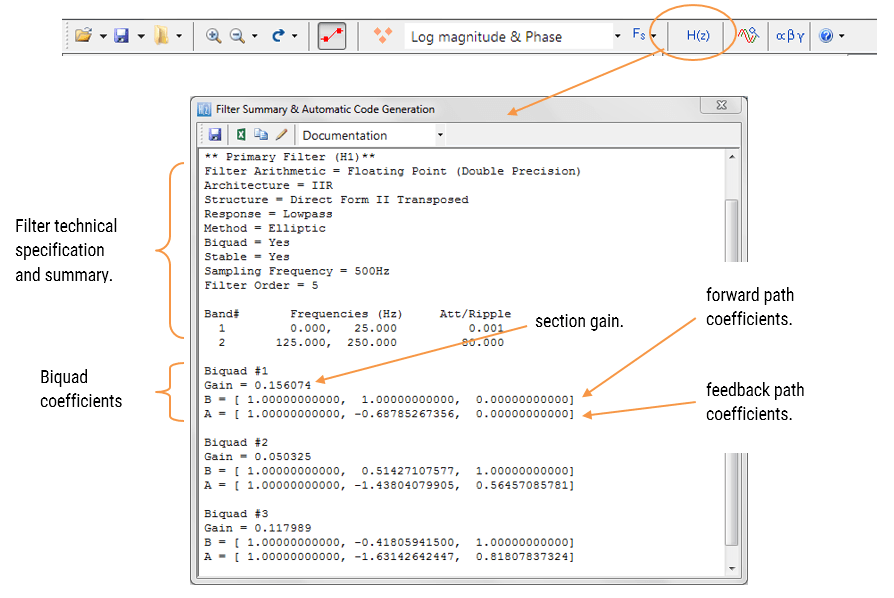
suodattimen Yhteenveto (esitetty kuvassa 4) tarjoaa suunnittelijalle yksityiskohtaisen yleiskuvan suunnitellusta suodattimesta, mukaan lukien yksityiskohtainen yhteenveto teknisistä eritelmistä ja suodatuskertoimista, joka esittelee nopean ja yksinkertaisen reitin suunnittelusi dokumentointiin.

ASN-Suodatinsuunnittelija tukee sekä single section-että biquad (default setting) IIR-suodattimien suunnittelua ja toteutusta.

Kuva 4: yksityiskohtainen erittely.

FIR määritelmä

palauttaen IIR: n lineaarisen vakiokertoimen erotusyhtälön, eli

\(\displaystyle
y(n)=\sum_{k=0}^{q}b_kx(n-k)-\sum_{k=1}^{p}a_ky (n-k)
\)

huomaa, että kun asetamme \(\small a_k\) kertoimet (eli palaute) nollaan, määritelmä vähentää alkuperäiseen fir-suodattimen määritelmään, mikä tarkoittaa, että FIR-laskenta perustuu vain menneisiin ja nykyisiin tuloihin, nimittäin:

\(\displaystyle
y(n)=\sum_{k=0}^{q}b_kx (n-k)
\)

toteutus

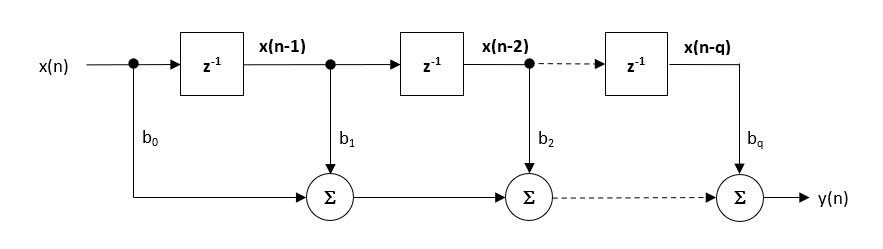
vaikka Kuusille on olemassa useita käytännön toteutuksia, suoramuotorakenne ja sen transponoitu serkku ovat ehkä yleisimmin käytettyjä, ja siksi kaikki suunnitellut suodatinkertoimet on tarkoitettu toteutettaviksi Suoramuotoisessa rakenteessa.

suoran muodon rakenne ja siihen liittyvä differenssiyhtälö on esitetty alla. Kiinteän pisteen toteutuksessa suoraa muotoa puoltaa yhden akun käsite.

\(\displaystyle y(n) = b_0x(n) + b_1x(n-1) + b_2x(n-2) + …. +b_qx(n-q) \)

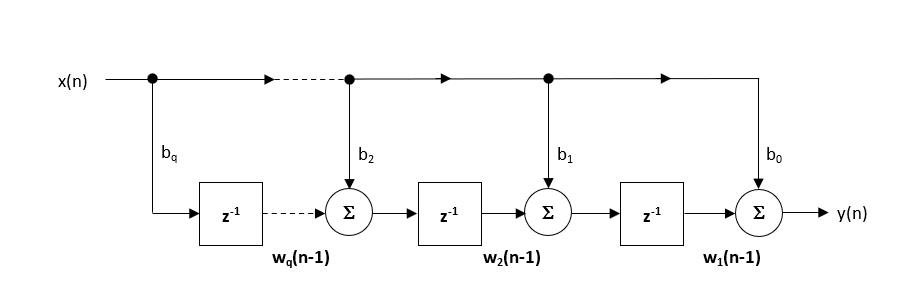
suositeltu (oletus) rakenne ASN suodatin suunnittelija on suora muoto Transposed rakenne, koska tämä tarjoaa erinomaisen numeerisen tarkkuuden käytettäessä liukuluku aritmeettinen. Tämä voidaan havaita analysoimalla alla olevia erotusyhtälöitä (joita käytetään toteutuksessa), koska numeerisen vaimennuksen ei-toivotut vaikutukset minimoidaan, koska liukulukujen yhteenlasku suoritetaan samansuuruisille luvuille.

\(\displaystyle \begin{eqnarray}y(n) & = &b_0x(n) &+& w_1(n-1) \\ w_1(n)&=&b_1x(n) &w_2(n-1) \ \ \ w_2(n)&=&b_2x(n)&+&w_3(n-1) \ \\vdots \quad& &\quad\vdots&+&\quad \ vdots \ \w_q(n)&=&b_qx(n) \ end{eqnarray}\)

What have We learned?

digitaaliset suodattimet jaetaan seuraaviin kahteen luokkaan:

• ääretön impulssivaste (IIR)
• äärellinen impulssivaste (FIR)

IIR (infinite impulse response) – suodattimet valitaan yleensä sovelluksiin, joissa lineaarinen vaihe ei ole liian tärkeä ja muisti on rajallinen. Niitä on käytetty laajalti äänen tasauksessa, biolääketieteellisessä anturisignaalin käsittelyssä, IoT/IIoT-älykkäissä antureissa ja nopeissa tietoliikenne/RF-sovelluksissa.

fir (finite impulse response) – suotimia valitaan yleensä sovelluksiin, joissa lineaarinen vaihe on tärkeä ja käytettävissä on kohtuullinen määrä muistia ja laskennallista suorituskykyä. Niillä on laajalti käytössä audio-ja biolääketieteellisissä signaalinparannussovelluksissa.

ASN Filter Designer tarjoaa insinööreille kaiken tarvittavan monimutkaisten IIR-ja FIR-digitaalisten suodattimien suunnitteluun, kokeiluun ja käyttöönottoon erilaisissa anturimittaussovelluksissa. Nämä edut yhdistettynä automaattiseen dokumentointiin ja koodin luomiseen mahdollistavat sen, että insinöörit voivat suunnitella ja validoida IIR/FIR-digitaalisen suodattimen muutamassa minuutissa eikä tunnissa.