käyttämällä logaritmeja reaalimaailmassa
logaritmeja on kaikkialla. Oletko koskaan käyttänyt seuraavia lauseita?
- 6 luvut
- kaksinumeroiset
- suuruusluokka
- korko
kuvaat lukuja niiden potenssien 10 eli logaritmin mukaan. Ja korko on sijoituksen kasvun logaritmi.
Yllätyitkö siitä, että logaritmit ovat niin yleisiä? Minä myös. Useimmat yritykset matematiikan reaalimaailmassa (TM) osoittavat logaritmit jossain arcane kaava, tai teeskennellä olemme geologeja kiehtonut Richter asteikko. ”Tutkijat välittävät lokit, ja sinunkin pitäisi. Voitko kuvitella maailmaa ilman sinkkiä?”
ei, ei, ei, ei, ei! (Mamma mia!)
matematiikka ilmaisee käsitteitä, joilla on notaatio kuten ”ln” tai ”log”. ”Matematiikan löytäminen reaalimaailmassa” tarkoittaa ideoiden kohtaamista elämässä ja sen näkemistä, miten ne voitaisiin kirjoittaa notaatiolla. Älä etsi kirjaimellisia symboleja! Milloin viimeksi kirjoitit jakokyltin? Milloin viimeksi pilkoit ruokaa?
Ok, ok, tajutaan: mistä logaritmeissa on kyse?
logaritmit löytävät syyn vaikutukselle, eli tulo jollekin tuotokselle
yleinen ”vaikutus” on nähdä jonkin kasvavan, kuten meneminen \$100: sta \$150: een 5 vuodessa. Miten tämä tapahtui? Emme ole varmoja, mutta logaritmi löytää mahdollisen syyn: jatkuva tuotto Ln(150/100) / 5 = 8,1% selittäisi tämän muutoksen. Se ei ehkä ole varsinainen syy (tapahtuiko kaikki kasvu viimeisenä vuonna?), mutta se on tasainen keskiarvo, jota voimme verrata muihin muutoksiin.
muuten ”syyn ja seurauksen” käsite on vivahteikas. Miksi 1000 on suurempi kuin 100?
- 100 on 10 joka kasvoi itsestään 2 ajanjaksoa ($10 * 10$)
- 1000 on 10 joka kasvoi itsestään 3 ajanjaksoa ($10 * 10 * 10$)
voimme ajatella numeroita tuotoksina (1000 on ”1000 tuotosta”) ja panoksina (”kuinka monta kertaa 10: n täytyy kasvaa, jotta nuo tuotokset saadaan aikaan?”). Joten,
1000 outputs > 100 outputskoska
3 inputs > 2 inputstai toisin sanoen:
log(1000) > log(100)miksi tämä on hyödyllistä?
logaritmit laittavat luvut ihmisystävälliselle asteikolle.
suuret luvut rikkovat aivomme. Miljoonat ja biljoonat ovat ”todella isoja”, vaikka miljoona sekuntia on 12 päivää ja biljoona sekuntia 30 000 vuotta. Se on ero amerikkalaisen lomavuoden ja koko ihmissivilisaation välillä.
temppu ”valtavan lukusokeuden” voittamiseksi on kirjoittaa numerot ”panosten” (eli niiden potenssipohjan 10) mukaan. Tämä pienempi asteikko (0-100) on paljon helpompi ymmärtää:
- teho 0 = $10^0$ = 1 (single item)
- teho 1 = $10^1$ = 10
- power of 3 = $10^3$ = tuhat
- power of 6 = $10^6$ = miljoona
- power of 9 = $10^9$ = miljardi
- power of 12 = $10^12$ = biljoona
- power of 23 = $10^23$ = molekyylien lukumäärä kymmenessä grammassa hiiltä
- teho 80 = $10^80$ = molekyylien lukumäärä maailmankaikkeudessa
a 0-80 asteikko vei meidät yhdestä aineesta maailmankaikkeuden asioiden lukumäärään. Ei hassumpaa.
logaritmit laskevat kertolaskun portaina
logaritmit kuvaavat kertolaskun muutoksia: yllä olevissa esimerkeissä jokainen askel on 10 kertaa suurempi. Luonnollisella lokilla jokainen askel on ” e ” (2,71828…) kertaa enemmän.
kun käsitellään useita kertolaskuja, logaritmit auttavat ”laskemaan” niitä, aivan kuten yhteenlasku laskee meille, kun efektejä lisätään.
Näytä Matikka
aika lihalle: katsotaan mihin logaritmit ilmaantuvat!
kuusinumeroinen palkka tai kaksinumeroinen kulu
kuvaamme lukuja niiden numeroiden mukaan, ts. kuinka monta valtaa 10 heillä on(ovat ne kymmeniä, satoja, tuhansia, kymmenen tuhansia, jne.). Numeron lisääminen tarkoittaa ”kertomista 10: llä”, ts.
![]()
logaritmit laskea useita kerrannaisia lisätään, joten alkaen 1 (yksi numero) lisäämme 5 numeroa ($10^5$) ja 100,000 saada 6-numeroinen tulos. Puhuminen ”6” sijasta ”satatuhatta” on logaritmien ydin. Se antaa karkean mittakaavan tunteen hyppäämättä yksityiskohtiin.
Bonuskysymys: Miten kuvailisit 500 000? ”6-luvun” sanominen on harhaanjohtavaa, koska 6-luvut tarkoittavat usein jotain lähempänä 100 000: ta. Toimisiko ”6,5-luku”?
ei oikeastaan. Meidän päässämme, 6.5 tarkoittaa ”puolivälissä” välillä 6 ja 7 lukuja, mutta se on adder ajattelutapa. Logaritmeilla a”.5 ” tarkoittaa kertolaskun suhteen puoltaväliä eli neliöjuurta ($9^.5$ tarkoittaa, että neliöjuuri 9 — 3 on puolessa välissä kertolaskun suhteen, koska se on 1-3 ja 3-9).
kun otetaan loki(500 000), saadaan 5.7, lisätään 1 lisänumeroon, ja voidaan sanoa ” 500 000 on 6.7 kuva numero”. Kokeile tästä:
suuruusluokka
me nörtit rakastamme tätä lausetta. Se tarkoittaa karkeasti ”10x ero”, mutta vain kuulostaa viileämpi kuin”1 numero suurempi”.
tietokoneissa, joissa kaikki lasketaan biteillä (1 tai 0), jokaisella bitillä on tuplausvaikutus (ei 10x). Joten menee 8-16 bittiä on ”8 kertaluokkaa” tai $2^8 = 256$ kertaa suurempi. (”Suurempi” viittaa tässä tapauksessa siihen muistin määrään, jota voidaan käsitellä.) Menee 16-32 bittiä tarkoittaa ylimääräistä 16 suuruusluokkaa, tai $2^16 $ ~ 65,536 kertaa enemmän muistia, joka voidaan käsitellä.
korot
miten kasvuluvut saadaan selville? Maa ei aio kasvaa 8,56 prosentin vuosivauhtia. Tarkastellaan BKT: tä yhtenä vuonna ja BKT: tä seuraavana, ja otetaan logaritmi löytää implisiittinen kasvuvauhti.
kaksi suosikkitulkintaani luonnollisesta logaritmista (Ln (x)), eli luonnollisesta logista 1.5:
- olettaen 100% kasvu, kuinka kauan sinun täytyy kasvaa päästä 1.5? (.405, alle puolet ajanjaksosta)
- olettaen 1 aikayksikkö, kuinka nopeasti sinun täytyy kasvaa päästäksesi 1.5: een? (40.5% vuodessa, jatkuvasti yhdistettyinä)
logaritmien avulla selvitämme, kuinka nopeasti kasvamme.
mittausasteikko: Google PageRank
Google antaa jokaiselle Webin sivulle pistemäärän (PageRank), joka on karkea arvovallan / merkityksen mittari. Tämä on logaritminen asteikko, joka minun päässäni tarkoittaa ”PageRank laskee numeroiden lukumäärän pisteessäsi”.
niinpä sivusto, jossa on pagerank 2 (”2 numeroa”), on 10x suositumpi kuin PageRank 1-sivusto. Sivustoni on PageRank 5 ja CNN on PageRank 9, joten siellä on ero 4 suuruusluokkaa($10^4$ = 10,000).
karkeasti sanottuna saan noin 7000 käyntiä päivässä. Kirjekuorimatematiikallani voin arvata, että CNN saa noin 7 000 * 10 000 = 70 miljoonaa käyntiä päivässä. Miten minä tuon tein? Päässäni ajattelen, että $7k * 10k = 70 * k * K = 70 * M$). Niillä saattaa olla muutaman kerran enemmän (100M, 200m), mutta ei luultavasti jopa 700M.
Google välittää paljon tietoa hyvin karkealla asteikolla (1-10).
mittausasteikko: Richter, desibeli jne.
huokaa. Olemme tyypillisessä ”logaritmit todellisessa maailmassa” esimerkissä: Richterin asteikko ja desibeli. Ajatuksena on laittaa tapahtumat, jotka voivat vaihdella rajusti (maanjäristykset) yhteen mittakaavaan pienellä alueella (tyypillisesti 1-10). Aivan kuten PageRank, jokainen 1 pisteen lisäys on 10x parannus tehossa. Suurin ihmiseltä mitattu maanjäristys oli 9,5; Jukatanin niemimaan isku, joka todennäköisesti teki dinosaurukset sukupuuttoon, oli 13.
desibelit ovat samanlaisia, joskin se voi olla negatiivinen. Äänet voivat mennä erittäin hiljainen (pisaran) erittäin kovaa (lentokone) ja aivomme voivat käsitellä kaiken. Todellisuudessa lentokoneen moottorin ääni on miljoonia (miljardeja, biljoonia) kertaa voimakkaampi kuin pisaran, ja on hankalaa saada asteikko, joka menee 1: stä gazillioniin. Lokit pitävät kaiken kohtuullisella tasolla.
logaritminen kuvaaja
näet usein ”log-asteikolla” piirrettyjä kohteita. Päässäni tämä tarkoittaa sitä, että toisella puolella lasketaan ” numeroiden määrää ”tai” kertolaskujen määrää”, ei itse arvoa. Jälleen tämä auttaa näyttämään villisti vaihtelevia tapahtumia yhdellä asteikolla (menee 1: stä 10: een, ei 1: stä miljardeihin).
Mooren laki on hyvä esimerkki: tuplaamme transistorien määrän 18 kuukauden välein (Kuva kohteliaisuus Wikipedia).
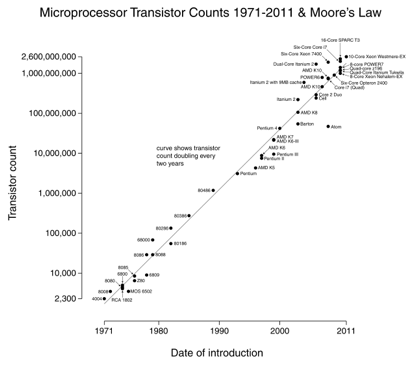
siisti asia lokiasteikon kuvaajissa on se, että eksponentiaaliset muutokset (suorittimen nopeus) näkyvät suorana. Kasvaa 10x vuodessa tarkoittaa olet tasaisesti marssivat ylös ”numeroa” asteikko.
eteenpäin ja ylöspäin
jos jokin käsite on hyvin tunnettu, mutta ei kovin rakastettu, se tarkoittaa, että meidän on rakennettava intuitiotamme. Etsi analogiat, jotka toimivat, äläkä tyydy moskaan, jota oppikirja ravaa. Päässäni:
- logaritmit etsi perussyy vaikutukselle (katso kasvu, etsi korko)
- ne auttavat laskemaan kertolaskuja tai numeroita, osittaisten laskujen bonuksena (500k on 6,7-numeroinen luku)
hyvää Matikkaa.
muita viestejä tässä sarjassa
- intuitiivinen opas Eksponentiaalisiin funktioihin & e
- luonnollisen logaritmin (ln) Demystifying
- visuaalinen opas yksinkertaisiin, yhdistettyihin ja jatkuviin korkoihin
- E: n yhteiset määritelmät (värillinen)
- eksponenttien ymmärtäminen (miksi 0^0 = 1?)
- logaritmien käyttäminen reaalimaailmassa
- miten ajatella Eksponenteilla ja Logaritmeilla
- diskreetin vs. jatkuvan kasvun ymmärtäminen
- mitä eksponentti todella tarkoittaa?
- Q: Miksi E on erityinen? (2.718… ei 2: ta, 3.7: ää tai muuta numeroa?)