Kdnuggets

By Sydney Firmin, Alteryx.

”pohjimmiltaan kaikki mallit ovat vääriä, mutta jotkut mallit ovat hyödyllisiä.”- George Box

tämä kuuluisa George Boxin sitaatti kirjattiin ensimmäisen kerran vuonna 1976 lehdessä ”Science and Statistics”, joka julkaistiin Journal of the American Statistical Association-lehdessä. Se on tärkeä lainaus tilastojen ja analyyttisten mallien alalla, ja se voidaan purkaa kahteen osaan.

Kaikki mallit ovat vääriä

tämän väitteen kaivamiseksi on määriteltävä ja tutkittava, mikä malli on.

tämän artikkelin yhteydessä Malli voidaan ajatella yksinkertaistettuna esityksenä järjestelmästä tai oliosta. Tilastolliset mallit likiarvostelevat aineistoa tekemällä oletuksia aineistosta sekä ympäristöstä, jossa se kerättiin ja johon sitä sovellettiin.

tilastollisten mallien kolme laajaa oletusluokkaa ovat jakaumaoletukset (oletukset muuttujan arvojen jakaumasta tai havaintovirheiden jakaumasta), rakenteelliset oletukset (oletukset muuttujien välisestä funktionaalisesta suhteesta) ja ristivaihteluoletukset (yhteinen todennäköisyysjakauma).

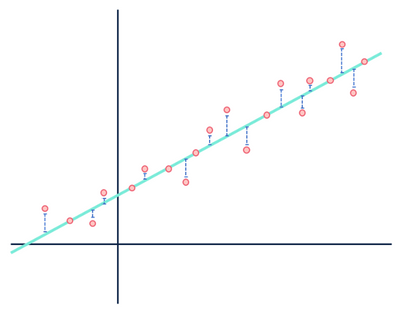
esimerkiksi lineaarinen regressiomalli olettaa, että tietojoukon muuttujien väliset suhteet ovat lineaarisia (ja vain lineaarisia). Lineaarisen mallin silmissä kaikki etäisyys tietojoukon muodostavien havaintojen ja mallinnetun viivan välillä on vain kohinaa (eli satunnaista tai selittämätöntä vaihtelua aineistossa), ja se voidaan lopulta jättää huomiotta.

älä välitä etäisyyksistä sinisellä.

George Box totesi, että kaikki mallit ovat väärässä nimenomaan tilastollisten mallien yhteydessä. Koska mallin luonne on yksinkertaistettu ja idealisoitu esitys jostakin, kaikki mallit ovat jossain mielessä väärässä. Mallit eivät koskaan ole ”totuus”, jos totuus tarkoittaa täysin todellisuuden edustamista. On erittäin tärkeää ottaa huomioon mallin luomisessa tehdyt oletukset, koska mallit ovat todella hyödyllisiä vain silloin, kun oletuksia pidetään yllä.

Kartat ja miniatyyrit

samanlaisia havaintoja kuin Boxin ”kaikki mallit ovat väärässä”on monilla eri aloilla.

on olemassa kartta-aluesuhteeseen viittaava aforismi, joka on liitetty Alfred Korzybskiin:

kartta ei ole se alue, jota se edustaa, mutta jos se on oikein, se on rakenteeltaan samanlainen kuin alue, mikä selittää sen käyttökelpoisuuden.

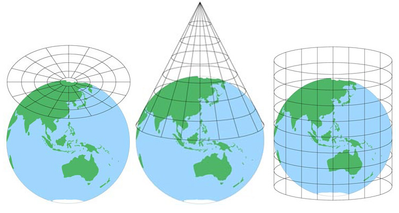
kartat ovat hyödyllisiä, koska ne ovat todellisen kohteen abstraktioita helpommin hallittavassa mittakaavassa, mutta ne jättävät aina pois jonkin yksityiskohtaisuuden tason. Riippuen siitä, kuinka paljon pinta-alaa kartta sisältää, voi myös olla jonkin verran vääristymiä johtuen projisoinnista kartan (aiheuttama hankala prosessi muuntaa pallomainen Maapallo Tasainen esitys).

(Kuvan lähde.)

ainoa todella tarkka kartta olisi 1: 1-toisinto sen edustamasta alueesta. Tuollaisesta kartasta ei kuitenkaan olisi sen enempää apua kuin itse alueella navigoimisesta.

harkitse lainausta runoilija Paul Valerylta:

kaikki yksinkertainen on valheellista. Kaikki monimutkainen on käyttökelvotonta.

Stanfordin liiketalouden professorin mukaan nimetty Boninin paradoksi kuvaa haastetta luoda hyödyllisiä, täydellisiä malleja tai simulaatioita monimutkaisista järjestelmistä. Mallin kehityksessä on usein tasapainoilua monimutkaisuuden ja tarkkuuden välillä. Jos mallin tavoitteena on selkeyttää suhdetta tai järjestelmää, kompleksisuuden lisääminen kumoaa tämän tarkoituksen (vaikka se saattaakin tehdä mallista tarkemman).

korkealla tasolla kartta-aluesuhde kuvaa myös kohteen ja kohteen esittämisen välistä suhdetta.

jos on joskus käynyt filosofian tunnilla, on saattanut törmätä surrealistitaiteilija Rene Magritten teokseen kuvien petollisuus.

teksti kääntyy muotoon ” tämä ei ole putki.”Eikä se ole. Emme voi tunkea tätä (digitaalista) kuvaa tupakkaan ja polttaa sitä, koska se on vain todellisen esineen esitys.

mallit ovat abstraktioita. Kuten kartat tai pienoisarkkitehtuurimallit tai kaaviot, ne eivät voi kuvata jokaista yksityiskohtaa kohteesta tai järjestelmästä, johon ne perustuvat, vaikka vain siksi, että niitä ei ole olemassa reaalimaailmassa eivätkä ne toimi samalla tavalla.

Jos Kaikki Mallit Ovat Väärässä, Miksi Vaivautua?

George Boxin aforismilta ei puutu kriitikoita.

Ongelma, joka monilla tilastotieteilijöillä on tämän lainauksen kanssa, näyttää jakaantuvan karkeasti kahteen kategoriaan:

1. mallien virheellisyys on ilmiselvä toteamus. Tietenkin kaikki mallit ovat väärässä, he ovat malleja.
2. tätä sitaattia käytetään tekosyynä huonoille malleille.

tilastotieteilijä J. Michael Steele on suhtautunut sanontaan kriittisesti (katso tämä henkilökohtainen essee). Steelen ensisijainen argumentti on, että” väärä ” tulee kuvaan vain, jos malli ei vastaa oikein kysymykseen, johon se väittää vastaavansa (esim., että kartassa oleva rakennus on merkitty väärin, ei niin, että rakennusta edustaa pieni neliö). Steele jatkaa:

suurin osa julkaistuista tilastollisista menetelmistä janoaa yhtä rehellistä esimerkkiä.

Steele väittää, että tilastolliset mallit eivät useinkaan yllä riittävään kuntomittaan, eivätkä monet tilastotieteilijöiden kehittelemät mallit ole riittäviä käyttötarkoitukseensa.

artikkelissa tilastot tieteenä, Ei taiteena: The Way to Survive in Data Science, Mark van der Laan (Statistics at UC Berkeley) pitää tekstiruutua osasyynä huonoihin tilastollisiin malleihin ja hylkää sen ”täydellisenä hölynpölynä.”Hän jatkaa kirjoittamista:

tilastojen perusta ( … ) ei voinut olla ”kätevän” tilastollisen mallin mielivaltainen valitseminen. Kuitenkin juuri niin useimmat tilastotieteilijät tekevät huolettomasti viitaten ylpeänä lainaukseen: ”kaikki mallit ovat väärässä, mutta jotkut ovat hyödyllisiä.”Tämän vuoksi mallit, jotka ovat niin epärealistisia, että ne on indeksoitu äärellisellä dimensioparametrilla, ovat edelleen status quo, vaikka kaikki ovat samaa mieltä siitä, että ne tiedetään epätosiksi.

ratkaisuna Van der Laan kehottaa tilastotieteilijöitä lopettamaan Boxin sitaatin käytön ja sitoutumaan ottamaan datan, tilastot ja tieteellisen menetelmän vakavasti. Hän kehottaa tilastotieteilijöitä käyttämään aikaa sen oppimiseen, miten tietyn tietoaineiston data on tuotettu, ja sitoutumaan kehittämään realistisia tilastollisia malleja koneoppimisen ja data-adaptiivisen estimointitekniikan avulla perinteisempien parametristen mallien sijaan.

tässä artikkelissa on tilastotieteilijöiden Michael Lavinen ja Christopher Tongin vastaukset sekä vastaus alkuperäisen kirjoittajan vastauksiin. Nämä kaksi kumoavaa tilastotieteilijää viittaavat esimerkkeihin, joissa mallien tiedetään olevan vääriä, mutta niitä käytetään usein, koska ne ovat hyödyllisiä ja sopivat tiettyyn ongelmaan. Heidän esimerkkejään ovat kolme erilaista valon mallia, jotka löytyvät Optiikan alalta (geometrinen optiikka, fysikaalinen optiikka ja kvanttioptiikka; kaikki kolme mallia edustavat valoa eri tavalla, ovat ”väärässä” jossain mielessä, ja niitä käytetään edelleen tänään), ja (lähes) lineaarinen suhde hiilivuon lokin ja maaperän lämpötilan välillä, joka löytyy Harvardin metsästä kerätyistä tiedoista.

Van der Laan puolestaan vastaa näihin esimerkkeihin ja muihin artikkelinsa arvosteluihin, erityisesti käsitykseensä ”oikean” mallin löytämisestä. Vastauskirjeet kannattaa ehdottomasti lukea, jos kiinnostaa. Tämä on aktiivinen keskustelunaihe tilastotieteen ja datatieteen aloilla.

mutta jotkut mallit ovat käyttökelpoisia

mallien rajoituksista huolimatta monet mallit voivat olla hyvinkin hyödyllisiä. Koska mallit ovat yksinkertaistettuja, ne ovat usein hyödyllisiä järjestelmän jonkin osan tai piirteen ymmärtämisessä.

datatieteen yhteydessä koneoppimisen ja tilastollisten mallien avulla voidaan arvioida (ennustaa) tuntemattomia arvoja. Monissa yhteyksissä, jos mallin oletukset pitävät, vahvan tilastollisen mallin tarjoama epävarma arvio voi silti olla erittäin hyödyllinen päätöksenteon kannalta.

George Boxin viisauden toinen, vähemmän siteerattu puolisko on tämä:

”käytännön kysymys on, kuinka väärin (mallien) pitää olla, jotta niistä ei ole hyötyä.”- George Box

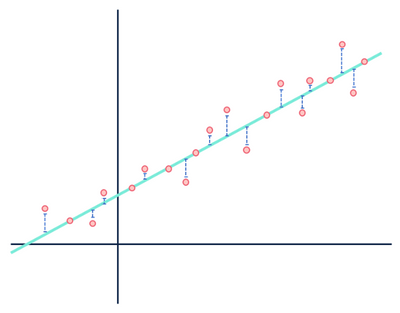
katsotaanpa taas lineaarista regressioesimerkkiä:

enimmäkseen käytin liikaa aikaa tähän kuvaan käyttääkseni sitä vain kerran.

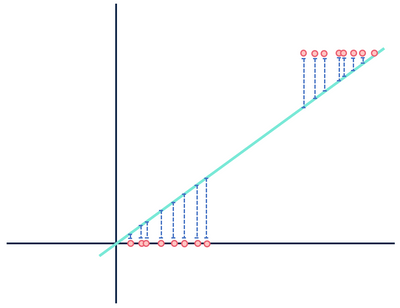
Katsotaanpa nyt toista teoreettista lineaarista regressiomallia, joka sopii eri aineistoon.

älkää välittäkö etäisyyksistä. odottakaa, tämä ei voi olla oikein.

molemmissa luvuissa on virhe, mutta toinen tietojoukko osoittaa selvästi lineaarisen suhteen, kun taas toinen on logistinen. Molemmat mallit ovat ”vääriä”, mutta toinen kaappaa selvästi todellisen suhteen muuttujien välillä, kun taas toinen ei, tehden toisesta hyödyllisen ja toisesta hyödyttömän. Etäisyyksien hylkääminen sinisenä kohinana on kohtuullista, jos tiedoilla on lineaarinen suhde, mutta tämä oletus hajoaa, kun suhde on erilainen toiminnallinen muoto kuin valitsemasi malli.

hyvien mallien tekeminen

se, että mallit ovat väärässä tai rajoittuneita siinä, mitä ne edustavat, saattaa tuntua itsestään selvältä monista mallien parissa työskentelevistä, mutta valitettavasti monet ihmiset eivät tajua sitä tai ajattele sitä paljon. Siksi koen, että mallia kehitettäessä on tärkeää pitää George Boxin sanat mielessä. Sitä ei pidä käyttää tekosyynä huonojen mallien rakentamiselle.

tarkempaa luettavaa varten Steelellä on hienoja luokkamuistiinpanoja: onko mallissa järkeä? entä onko mallissa mitään järkeä? II osa: riittävyyden hyödyntäminen. Toinen suuri voimavara on paperi ’ kaikki mallit ovat väärässä…’: johdatus mallin epävarmuuteen mallivalintatyöpajasta, joka pidettiin vuonna 2011 Groningenissa.

toinen mielenkiintoinen lukema on When All Models are Wrong from Issues in Science and Technology, joka kehottaa Boxin sanoja tiukempaan avoimuuteen tieteellisissä ja tilastollisissa malleissa.

kaikesta tästä on tärkeää ottaa pois se, että ymmärtää, mitkä osa-alueet ovat mallisi kaappaamia ja mitkä eivät. On tärkeää tarkistaa oletukset ja lähtökohdat. Tilastotieteilijänä tai datatieteilijänä sinun vastuullasi on tuottaa tiukkoja malleja sekä tietää niiden rajoitukset. Ilmoita aina epävarmuutesi sekä mallisi laajuus. Tämä mielessä, voit tehdä malleja, jotka, vaikka mahdollisesti väärä, voi varmasti olla hyödyllinen.

Alkuperäinen. Lähetetään uudelleen luvalla.

Bio: Maantieteilijä koulutuksen ja data geek sydän, Sydney vahvasti sitä mieltä, että data ja tieto ovat arvokkaimpia, kun ne voidaan selkeästi kommunikoida ja ymmärtää. Nykyisessä roolissaan Sr. Data Science-Sisältöinsinöörinä hän saa viettää päivänsä tehden sitä, mitä hän rakastaa eniten; muuttamalla teknistä tietämystä ja tutkimusta mukaansatempaavaksi, luovaksi ja hauskaksi sisällöksi Alteryx-yhteisölle.

sukua:

• 3 suurinta virhettä datatieteen oppimisessa
• 3 isoa ongelmaa Big Datan kanssa ja niiden ratkaiseminen
• valinta Mallikandidaattien välillä