Piilotettu Markov malli: yksinkertainen määritelmä & yleiskatsaus

tilastojen määritelmät >

Piilotettu Markovin malli (HMM) on suhteellisen yksinkertainen tapa mallintaa peräkkäisiä tietoja. Piilotettu Markov malli tarkoittaa, että Markovin malli taustalla tiedot on piilotettu tai tuntematon sinulle. Tarkemmin sanottuna, tunnet vain havaintoaineistoa etkä tietoa valtioista. Toisin sanoen, on olemassa tietyntyyppinen malli, joka tuottaa dataa (Markovin malli), mutta et tiedä, mitkä prosessit tuottavat sitä. Periaatteessa käytät tietoasi Markovin malleista tehdäksesi valistuneen arvauksen mallin rakenteesta.

mikä on Markovin malli?

löytääkseen piilotetun Markovin mallin on ensin ymmärrettävä, mikä Markovin malli ylipäätään on. Täällä luon yksinkertaisen esimerkin käyttämällä kahta tuotetta, jotka ovat hyvin tuttuja todennäköisyys: noppaa ja pussit värillisiä palloja.

mallin komponentit, joita käytät satunnaisen mallin luomiseen, ovat:

• kuusisivuinen punainen stanssi.
• kymmenpuoleinen musta suulake.
• punainen pussi, jossa on kymmenen palloa. Yhdeksän palloa on punaisia, yksi musta.
• musta kassi, jossa oli kaksikymmentä palloa. Yksi pallo on punainen, yhdeksäntoista musta.

”musta” ja ”punainen” ovat kaksi valtiota tässä mallissa (toisin sanoen, voit olla musta, tai voit olla punainen).
luo nyt malli näitä vaiheita seuraamalla:

1. EMISSION vaihe: Roll kuolee. Huomaa numero, joka tulee esiin. Tämä on päästö. Yllä olevassa graafisessa, valitsin punainen kuolla aloittaa (mielivaltainen – olisin voinut valita musta) ja rullattu 2.
2. SIIRTYMISVAIHE: valitse satunnaisesti pussista pallo, jonka väri vastaa vaiheessa 1 rullaamaasi muottia. Rullasin punaisen diilin, joten valitsen pallon punaisesta pussista. Vedin esiin mustan pallon,joten siirryn seuraavaan päästöön.

näitä vaiheita voi sitten toistaa tietyn päästömäärän verran. Esimerkiksi tämän vaiheiden sarjan toistaminen 10 kertaa saattaa antaa joukon {2,3,6,1,1,4,5,3,4,1}. Prosessia, jossa siirrytään tilasta toiseen, kutsutaan Markovin prosessiksi.

siirtyminen punaisesta mustaan tai mustasta punaiseen kantaa erilaisia todennäköisyyksiä, koska pusseissa on eri määrä mustia ja punaisia palloja. Seuraavassa kaaviossa esitetään todennäköisyydet tälle nimenomaiselle mallille, jolla on kaksi tilaa (musta ja punainen):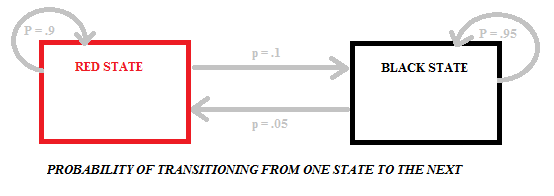

Piilotettu Markovin mallimerkintä

λ = (A,B,π) on pikakirjoitusmerkintä hmm: lle. Muita merkintää käytetään piilotetuissa Markovin malleissa:

• a = tilasiirtymätodennäköisyydet (aj)
• B = havainnon todennäköisyysmatriisi (bj(k))
• n = tilojen lukumäärä mallissa {1,2…n} tai tila ajankohtana t →st
• M = erillisten havaintosymbolien lukumäärä tilaa kohti
• Q = {q0 Q1,. . . , qN−1} = Markovin prosessin erilliset tilat
• T = havaintojakson pituus
• V = {0, 1, . . . , M − 1} = mahdollisten havaintojen joukko
• O = (O0, O1,. . . , OT -1) = havaintosekvenssi
• π = alkutilajakauma (ni)
• s = tila-tai tilajakauma (s1, s2… Sn)
• xk = piilotila
• zk = havainto.

kolme perusongelmaa

kolme perusongelmaa voidaan ratkaista piilotetuilla Markovin malleilla:

1. koska piilotettu Markov Modelλ = (A, B, π) ja sekvenssi havaintoja O, löytää todennäköisyys havainnon P(O | λ). Tätä kutsutaan joskus Arviointiongelmaksi.
2. kun otetaan huomioon Piilotettu Markovin Modelλ = (A, B, π) ja havaintosarja O, löydetään todennäköisin tilasekvenssi (s1, s2… Sn). Tätä kutsutaan joskus Dekoodausongelmaksi.
3. Etsi havaintojono (O1, O2…on ja piilotettu Markovin malli λ = (A, B, π), joka maksimoi o: n todennäköisyyden.tätä kutsutaan joskus Oppimisongelmaksi tai Optimointiongelmaksi.

Rabiner, L. R. ”opetusohjelma piilotettu Markov malleja ja valitut sovellukset puheentunnistus”, Proceedings of the IEEE, vol.77, s.257-286, Helmikuu. 1989.
Stamp, M. (2013). Paljastava Johdatus Piilotettu Markov malleja. Viitattu 8.6.2013 alkaen: http://www.cs.sjsu.edu/~stamp/RUA/HMM.pdf

——————————————————————————

Tarvitsetko apua kotitehtävissä tai koekysymyksessä? Chegg Studyn avulla saat askelmittaisia ratkaisuja kysymyksiisi alan asiantuntijalta. Ensimmäinen 30 minuuttia Chegg tutor on ilmainen!