Ympyrä jakautuu tasaisesti kuuteen yhtä suureen kolmioon

Hei Marilynn,

ensin kerron oletukseni siitä, miltä kuvasi näyttää:

1. jokaisella kolmiolla on ympyrän keskipisteessä kärki (kulma)
2. jokaisella kolmiolla on kulmat ympyrän kehällä (joten jokaisen kolmion kaksi sivua on säde)
3. kolmiot jakavat sivut (kolmioiden välillä ei ole gapeja)

kokonaiskuva näyttää kukalta – jokainen kolmio on terälehti.

tuntematon alue on se, mitä jää ympyrän ulkopuolelle, kehän ja ulkopuolen väliin kunkin kolmion. Tämä tuntematon alue on jaettu kuuteen congruent osioihin (yhtä suuri kaikin tavoin – kuten kolmiot ovat ”yhtä” kaikin tavoin – mukaan lukien alue, sivun pituus ja kaaren pituus). Ei ole selvää, Tarkoitatko, että yhden kaaren pinta-ala on Pi (ei oikeastaan split Pie, vaikka pronouched sama), vai kaikki kuusi osaa yhdessä on Pi. Seuraavassa oletan, että jonkin ulko-osan pinta-ala on Pi, niin että kaikkien kuuden osan pinta-ala yhteensä on 6 kertaa Pi. Meidän on löydettävä ympyrän säde, kutsuttava sitä r: ksi.

käytän myös P: tä tarkoittamaan Pi: tä (tai n. 3.14). Nyt on paljon tietoa, jota voimme koristella kolmioista.:

1. keskipisteen kulmat ovat kaikki 60 astetta. Tämä johtuu siitä, että keskipisteen kuusi kulmaa ovat kaikki yhtä suuret, ja ympyrällä on 360 astetta. Samoin on 360: n eduksi 6.
2. jokainen kolmio on tasakylkinen. Tämä johtuu siitä, että kaksi puolta ovat yhtä suuret (sivut, jotka ovat säde).
3. jokainen kolmio on itse asiassa tasasivuinen. Koska kyseessä on iscoceles, myös kaksi ulkokulmaa ovat yhtä suuret. Mutta kolmiossa on 180 astetta, keskuskulmassa käytetään jo 60: tä, jolloin ulkokulmille jää 180-60=120 astetta. Mutta 120 jaettuna 2: lla on 60 astetta, joten kaikki kolme kulmaa ovat yhtä suuret, joten se on isoscles.
4. jokaisen kolmion jokainen sivu on pituudeltaan r. Tämä johtuu siitä, että meillä on 6 congruent (”equal” kaikin tavoin) tasasivuiset kolmiot, ja koska kaksi puolta jokaisen kolmion on säde.

kolmioiden geometriasta on tehtävä jonkin verran algebraa. Koska tiedämme alueen, ja tarvitsemme säde, tarvitsemme kaava (tai yhtälö) säde kannalta alueen (mitä seuraa, pitää tavoite kaava mielessä). Ympyrän pinta-ala on P*r2 (r2 tarkoittaa R neliöön, ja * tarkoittaa moninkertaistaa) alueen, joka on jäänyt osien ulkopuolella kolmiot, mutta sisällä ympyrä (alue emme jo ole 6*P), voidaan myös löytää vähentämällä alueen kolmiot alueen ympyrän. Meidän täytyy löytää alueen yksi tasasivuiset kolmiot.

menetelmä 1 laskettaessa kolmion pinta-alaa
kolmion pinta-ala on B*h/2 tässä tarvitaan jonkin verran trigonometriaa: piirretään kärkipisteestä viiva vastakkaiselle puolelle, joka jakaa vastakkaisen puolen kahtia ja on suorassa kulmassa. Tämä jakaa tasasivuisen kolmion kahteen congruent oikeus kulma kolmiot, ja uusi puoli on korkeus, kutsua sitä h. meidän täytyy löytää h.

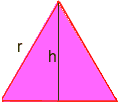
käyttämällä trig on yksi oikeus kulma kolmiot, meillä on sin60 = h / r mutta sin60 = sqr(3)/2, jossa sqr(3) tarkoittaa neliöjuuri kolme niin sqr(3)/2 = h/r kerrotaan molemmin puolin R saada h = r*sqr(3)/2 R nyt, pinta-ala yhden tasasivuisen kolmion on b*h/2 = (r)*(r*sqr(3)/2)/2 = (r2)*sqr (3)/4 r = sqr(6*P/(P-6*sqr(3) / 4)) Käytä laskimen laskemiseen leikkausjärjestystä (P=3.14): r= 5.896… Ympyrän säde on siis n. 5.9. Paul