forskel mellem IIR-og FIR-filtre: en praktisk designguide
et digitalt filter er en matematisk algoritme, der fungerer på et digitalt datasæt (f.eks. Anvendelser af denne type teknologi inkluderer fjernelse af fejl fra sensordata eller endda oprydning af støj på et målt signal for lettere dataanalyse. Men hvordan vælger vi den bedste type digitalt filter til vores applikation? Hvad er forskellen på et IIR-filter og et FIR-filter?
digitale filtre er opdelt i følgende to kategorier:
- uendelig impulsrespons (IIR)
- endelig impulsrespons (FIR)
som navnene antyder, kategoriseres hver type filter efter længden af dets impulsrespons. Men før du begynder med en detaljeret matematisk analyse, er det klogt at sætte pris på forskellene i ydeevne og egenskaber for hver type filter.
eksempel
for at illustrere forskellene mellem en IIR og FIR er frekvensresponsen for en 14.ordens FIR (solid linje) og en 4. ordens Chebyshev Type i IIR (stiplet linje) vist nedenfor i Figur 1. Bemærk, at selvom størrelsesspektre har en lignende grad af dæmpning, er fasespektret for IIR-filteret ikke-lineært i passbåndet (\(\lille 0\højre pil7, 5\)) og bliver meget ikke-lineær ved afskæringsfrekvensen, \(\lille f_c=7,5 h\). Bemærk også, at FIR kræver et højere antal koefficienter (15 vs IIR ‘ s 10) for at matche dæmpningskarakteristika for IIR.
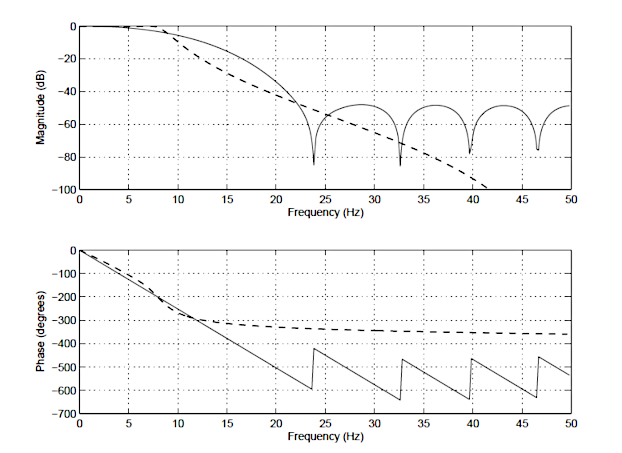
dette er blot nogle af forskellene mellem de to typer filtre. En detaljeret oversigt over de vigtigste fordele og ulemper ved hver type filter følger nu.
IIR-filtre
IIR (infinite impulse response) – filtre vælges generelt til applikationer, hvor lineær fase ikke er for vigtig, og hukommelsen er begrænset. De er blevet udbredt i lydudligning, biomedicinsk sensor signalbehandling, IoT/IIoT smarte sensorer og højhastigheds telekommunikation/RF applikationer.
fordele
- lave implementeringsomkostninger: kræver mindre koefficienter og hukommelse end FIR-filtre for at tilfredsstille et lignende sæt SPECIFIKATIONER, dvs.afskæringsfrekvens og stopbåndsdæmpning.
- lav latenstid: velegnet til realtidskontrol og RF-applikationer med meget høj hastighed i kraft af det lave antal koefficienter.
- Analog ækvivalent: kan bruges til at efterligne egenskaberne ved analoge filtre ved hjælp af s-å-plankortlægningstransformationer.
ulemper
- ikke-lineære fasekarakteristika: Fasekarakteristika for et IIR-filter er generelt ikke-lineære, især nær afskæringsfrekvenserne. All-pass udligningsfiltre kan bruges til at forbedre passband faseegenskaber.
- mere detaljeret analyse: kræver mere skalering og numerisk overløbsanalyse, når den implementeres i fast punkt. Den direkte form II filterstruktur er særlig følsom over for virkningerne af kvantisering og kræver særlig pleje i designfasen.
- numerisk stabilitet: Mindre numerisk stabil end deres fir (finite impulse response) modstykker på grund af feedbackstierne.
FIR-filtre
FIR (finite impulse response) – filtre vælges generelt til applikationer, hvor lineær fase er vigtig, og en anstændig mængde hukommelse og beregningsydelse er tilgængelig. De har en bredt implementeret i lyd-og biomedicinske signalforbedringsapplikationer. Deres all-nul struktur (diskuteret nedenfor) sikrer, at de aldrig bliver ustabile for nogen form for indgangssignal, hvilket giver dem en klar fordel i forhold til IIR.
fordele
- lineær fase: FIRs kan let designes til at have lineær fase. Dette betyder, at der ikke indføres nogen faseforvrængning i signalet, der skal filtreres, da alle frekvenser forskydes i tid med den samme mængde – hvilket opretholder deres relative harmoniske forhold (dvs.konstant gruppe og faseforsinkelse). Dette er bestemt ikke tilfældet med IIR-filtre, der har en ikke-lineær fasekarakteristik.
- stabilitet: da FIRs ikke bruger tidligere outputværdier til at beregne deres nuværende output, dvs. de har ingen feedback, de kan aldrig blive ustabile for nogen form for indgangssignal, hvilket giver dem en klar fordel i forhold til IIR-filtre.
- vilkårlig frekvensrespons: Parks-McClellan og ASN FilterScript ‘ s firarb () – funktion muliggør design af en gran med en vilkårlig størrelsesrespons. Det betyder, at en gran lettere kan tilpasses end en IIR.
- Fastpunktsydelse: virkningerne af kvantisering er mindre alvorlige end virkningerne af en IIR.
ulemper
- højt beregnings-og hukommelsesbehov: FIRs kræver normalt mange flere koefficienter for at opnå en skarp afskæring end deres IIR-kolleger. Konsekvensen af dette er, at de kræver meget mere hukommelse og betydeligt en højere mængde MAC (flere og akkumulere) operationer. Imidlertid inkluderer moderne mikrocontroller-arkitekturer baseret på armens hjernebark-m-kerner nu DSP-udstyrsstøtte via SIMD (signalinstruktion, flere data), der fremskynder filtreringsoperationen markant.
- højere latenstid: det højere antal koefficienter betyder, at en gran generelt er mindre egnet end en IIR til hurtige applikationer med høj kapacitet. Dette bliver problematisk for applikationer med lukket sløjfe i realtid, hvor et FIR-filter kan have for meget gruppeforsinkelse til at opnå sløjfestabilitet.
- ingen analog ækvivalent: ved hjælp af den Bilinære, matchede å-transformation (s-å-kortlægning) kan et analogt filter let omdannes til et ækvivalent IIR-filter. Dette er dog ikke muligt for en gran, da den ikke har nogen analog ækvivalent.
matematiske definitioner
som diskuteret i indledningen stammer navnet IIR og FIR fra de matematiske definitioner af hver type filter, dvs. et IIR-filter er kategoriseret efter dets teoretisk uendelige impulsrespons,
y (n)= \ sum_{k=0}^{\infty}h (k) h (n-k)
\)
og en FIR kategoriseret efter dens endelige impulsrespons,
y (n)= \ sum_{k=0}^{N-1}h(k)h (n-k)
\)
vi vil nu analysere de matematiske egenskaber for hver type filter igen.
IIR definition
som set ovenfor er et IIR-filter kategoriseret efter dets teoretisk uendelige impulsrespons,
\(\displaystyle y(n)=\sum_{k=0}^{\infty}h(k)h (n-k) \)
Praktisk set er det ikke muligt at beregne output fra en IIR ved hjælp af denne ligning. Derfor kan ligningen omskrives i form af et endeligt antal poler \(\lille p\ ) og nuller \(\lille K\), som defineret af lineær konstant koefficient forskel ligning givet af:
y (n)= \ sum_{k=0}^{K}b_k h (n-k)- \ sum_{k=1}^{p}a_ky(n-k)
\)
hvor, \(\small a_k\) og \(\small b_k\) er filterets nævner og tæller polynomiske koefficienter, hvem er rødder er lig med filterets poler og nuller henholdsvis. Således kan et forhold mellem forskelligningen OG Å-transformationen (overførselsfunktion) derfor defineres ved anvendelse af å-transformeringsforsinkelsesegenskaben sådan, at,
\sum_{k=0}^{q}b_kx(n-k)-\sum_{k=1}^{p}a_ky(n-k)\quad\stackrel{\displaystyle\mathcal{Z}}{\longleftrightarrow}\quad\frac{\sum\limits_{k=0}^b_k^{- k}} {1 + \ sum \ limits_{k=1}^p a_k^{- k}}
\)
som det ses, er overførselsfunktionen en frekvensdomænerepræsentation af filteret. Bemærk også, at polerne virker på outputdataene og nullerne på inputdataene. Da polerne virker på outputdataene og påvirker stabiliteten, er det vigtigt, at deres radier forbliver inde i enhedscirklen (dvs. <1) for BIBO (afgrænset input, afgrænset output) stabilitet. Nullernes radier er mindre kritiske, da de ikke påvirker filterstabiliteten. Dette er den primære årsag til, at alle nul FIR (finite impulse response) filtre altid er stabile.
BIBO stabilitet
et linear time invariant (LTI) system (såsom et digitalt filter) siges at være afgrænset input, afgrænset output stabilt eller BIBO stabilt, hvis hver afgrænset input giver anledning til en afgrænset output, som
\(\displaystyle \sum_{k=0}^{\infty}\left|h(k)\right|<\infty \)
hvor, \(\lille h(k)\) er LTI-systemets impulsrespons. Ved at analysere denne ligning skal det være klart, at BIBO-stabilitetskriteriet kun vil blive opfyldt, hvis systemets poler ligger inde i enhedscirklen, da systemets ROC (konvergensregion) skal omfatte enhedscirklen. Derfor er det tilstrækkeligt at sige, at et afgrænset indgangssignal altid vil producere et afgrænset udgangssignal, hvis alle polerne ligger inde i enhedscirklen.
nullerne på den anden side er ikke begrænset af dette krav og kan som følge heraf ligge hvor som helst på å-plan, da de ikke direkte påvirker systemstabiliteten. Derfor kan en systemstabilitetsanalyse foretages ved først at beregne rødderne af overførselsfunktionen (dvs.rødder af tælleren og nævneren polynomer) og derefter plotte de tilsvarende poler og nuller på å-planet.
en interessant situation opstår, hvis nogen poler ligger på enhedscirklen, da systemet siges at være marginalt stabilt, da det hverken er stabilt eller ustabilt. Selvom marginalt stabile systemer ikke er BIBO-stabile, er de blevet udnyttet af digitale oscillatordesignere, da deres impulsrespons giver en enkel metode til generering af sinusbølger, som har vist sig at være uvurderlige inden for telekommunikation.
Bikvad IIR-filtre
IIR-filterimplementeringen diskuteret heri siges at være bikvad, da den har to poler og to nuller som illustreret nedenfor i figur 2. Bikvadimplementeringen er især nyttig til implementering af faste punkter, da virkningerne af kvantisering og numerisk stabilitet minimeres. Imidlertid, den samlede succes for enhver bikvadimplementering afhænger af den tilgængelige nummerpræcision, som skal være tilstrækkelig nok til at sikre, at de kvantificerede poler altid er inde i enhedscirklen.
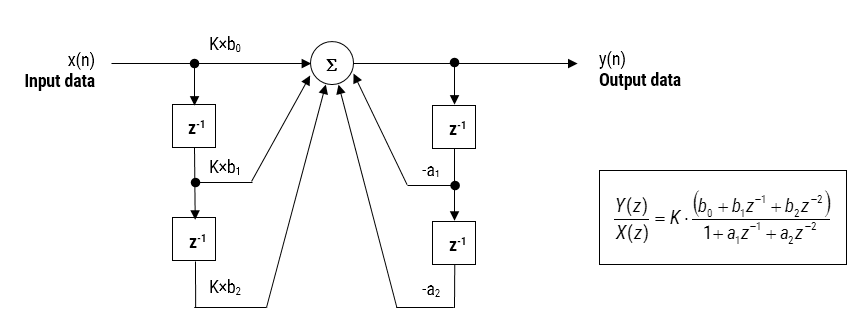
figur 2: direkte Form I (bikvad) IIR filter realisering og overførsel funktion.
analyse af figur 2 kan det ses, at bikvadstrukturen faktisk består af to feedbackstier (skaleret af \(\small a_1\) og \(\small a_2\)), tre fremføringsstier (skaleret af \(\small b_0, b_1\) og \(\small b_2\)) og en sektionsgevinst, \(\small K\). Således kan filtreringsoperationen i Figur 1 opsummeres ved hjælp af følgende enkle rekursive ligning:
\(\displaystyle y (n)=K\gange \ Big-a_1 y (n-1) – a_2 y(n-2)\)
analyse af ligningen, bemærk, at bikvad-implementeringen kun kræver fire tilføjelser (kræver kun en akkumulator) og fem multiplikationer, som let kan rumme på enhver mikrocontroller. Afsnittet gain, \(\small K\) kan også være pre-ganget med de fremadrettede sti koefficienter før implementering.
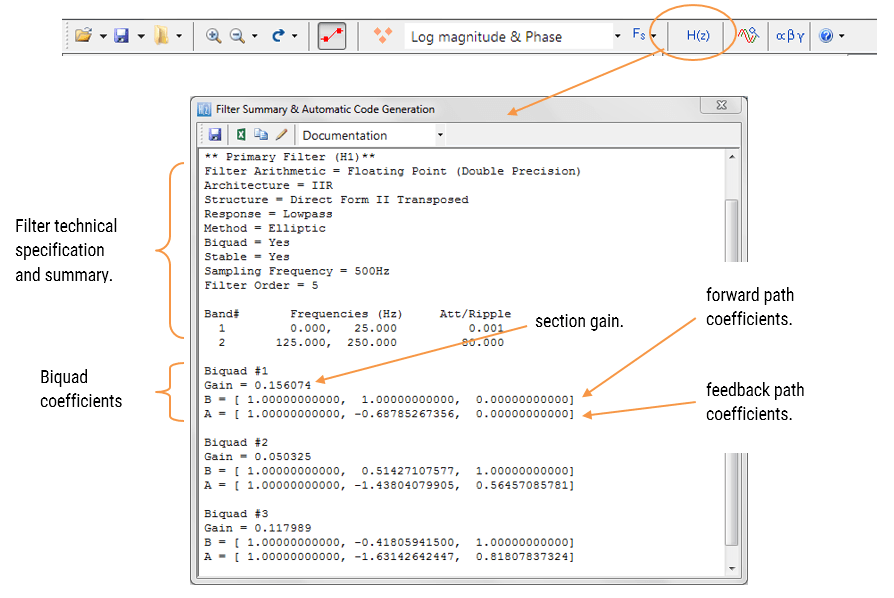
en samling af Bikvadefiltre kaldes en Bikvadkaskade, som illustreret nedenfor.

ASN Filter Designer kan designe og implementere en kaskade på op til 50 bikuber (kun professionel udgave).
Floating point implementering
ved implementering af et filter i floating point (dvs.ved anvendelse af dobbelt eller enkelt præcision aritmetik) direkte Form II strukturer anses for at være et bedre valg end den direkte Form i struktur. Den direkte form II transponerede struktur betragtes som den mest numerisk nøjagtige til implementering af flydende punkt, da de uønskede virkninger af numerisk svømning minimeres set ved at analysere forskelligningerne.
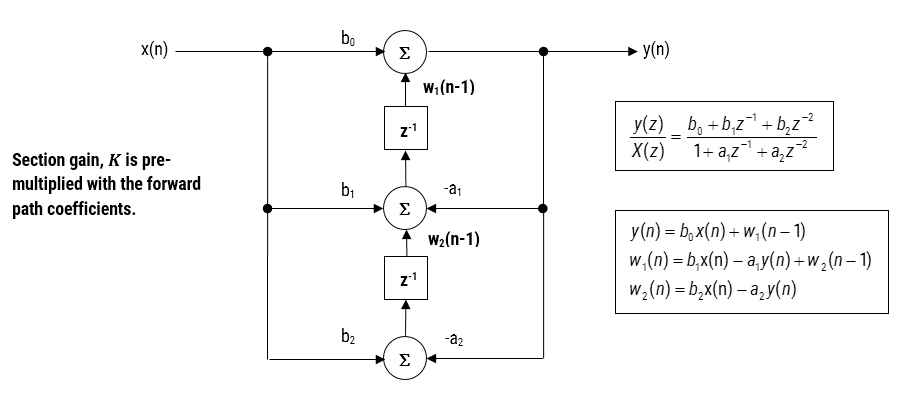
figur 3-direkte Form II transponeret strucutre, overførselsfunktion og forskelligninger
filteroversigten (vist i figur 4) giver designeren en detaljeret oversigt over det designede filter, herunder en detaljeret oversigt over de tekniske specifikationer og filterkoefficienterne, som præsenterer en hurtig og enkel rute til dokumentation af dit design.
ASN Filter Designer understøtter design og implementering af både enkelt sektion og Bikvad (standardindstilling) IIR filtre.
FIR definition
returnering af IIR ‘ ens lineære konstant koefficientforskelligning, dvs.
y(n)=\sum_{k=0}^{K}b_ks_(n-k)-\sum_{k=1}^{p}a_ky(n-k))
\)
Bemærk, at når vi indstiller \(\small a_k\) koefficienterne (dvs. feedbacken) til nul, reduceres definitionen til vores oprindelige FIR-filterdefinitionen, hvilket betyder, at FIR-beregningen kun er baseret på tidligere og nuværende inputværdier, nemlig:
y (n)= \ sum_{k=0}^{K}b_ks_ (n-k)
\)
implementering
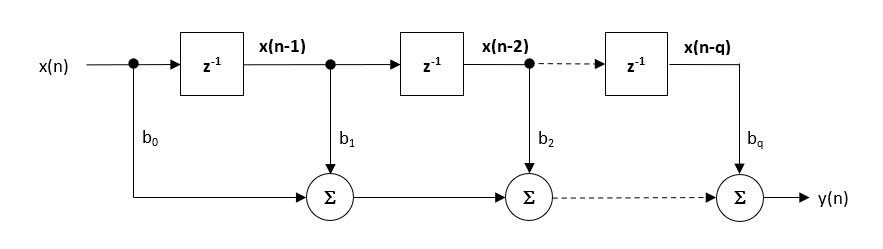
selvom der findes flere praktiske implementeringer til FIRs, er den direkte formstruktur og dens transponerede fætter måske den mest anvendte, og som sådan er alle designede filterkoefficienter beregnet til implementering i en direkte formstruktur.
den direkte formstruktur og tilhørende forskelligning er vist nedenfor. Den direkte Form anbefales til implementering af fast punkt i kraft af det enkelte akkumulatorkoncept.
\(\displaystyle y(n) = b_0h(n) + b_1h(n-1) + b_2h (n-2) + …. +b_k(n-k) \)
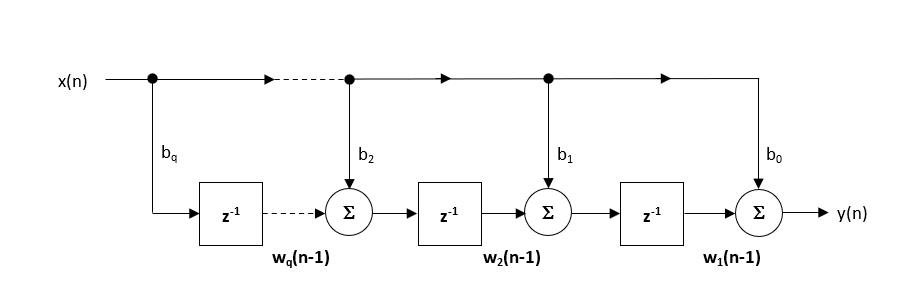
den anbefalede (standard) struktur inden for ASN-Filterdesigneren er den direkte Formtransponerede struktur, da dette giver overlegen numerisk nøjagtighed, når du bruger flydende aritmetik. Dette kan let ses ved at analysere forskellen ligninger nedenfor (bruges til implementering), da de uønskede virkninger af numerisk svømning minimeres, da tilsætning af flydende punkt udføres på tal af lignende størrelse.
\(\displaystyle \begin{eknarray}y(n) & = &b_0h(n) &+& V_1(n-1) \\ V_1(n)&=&b_1h(n) &+& v_2(n-1) \\ v_2(n)&=&b_2h(n) &+& v_3(n-1) \\ \vdots\fird &=& \firdot\vdots &+&\firdot\vdots \\ v_h(n)&=&Jørgensen}\)
Hvad har vi lært?
digitale filtre er opdelt i følgende to kategorier:
- uendelig impulsrespons (IIR)
- endelig impulsrespons (FIR)
IIR (infinite impulse response) filtre vælges generelt til applikationer, hvor lineær fase ikke er for vigtig, og hukommelsen er begrænset. De er blevet udbredt i lydudligning, biomedicinsk sensor signalbehandling, IoT/IIoT smarte sensorer og højhastigheds telekommunikation/RF applikationer.
FIR (finite impulse response) filtre vælges generelt til applikationer, hvor lineær fase er vigtig, og en anstændig mængde hukommelse og beregningsydelse er tilgængelig. De har en bredt implementeret i lyd-og biomedicinske signalforbedringsapplikationer.
ASN Filter Designer giver ingeniører med alt, hvad de har brug for at designe, eksperimentere og implementere komplekse IIR og FIR digitale filtre til en række sensor måling applikationer. Disse fordele kombineret med automatisk dokumentation og kodegenereringsfunktionalitet giver ingeniører mulighed for at designe og validere et IIR/FIR digitalt filter inden for få minutter snarere end timer.
