Bootstrap dans R

Bootstrap est une méthode d’inférence sur une population à l’aide de données d’échantillon.Bradley Efron l’a présenté pour la première fois dans cettepapier en 1979.Bootstrap repose sur l’échantillonnage avec remplacement à partir de données d’échantillons. Cette technique peut être utilisée pour estimer l’erreur-type de n’importe quelle statistique et pour lui attribuer un intervalle de confiance (IC). Bootstrap est particulièrement utile lorsque CI n’a pas de forme fermée, ou qu’il en a une très compliquée.

Supposons que nous ayons un échantillon de n éléments: X = {x1, x2, …, xn} et nous nous intéressons à CI pour une statistique T = t(X). Bootstrapframework est simple. Nous répétons simplement R fois le schéma suivant: Pour la i-th répétition, échantillonnez avec n éléments de remplacement de l’échantillon disponible (certains d’entre eux seront sélectionnés plus d’une fois). Appelez ce nouvel échantillon i-th échantillon d’amorçage, Xi, et calculatedesired statistic Ti = t(Xi).

Par conséquent, nous obtiendrons les valeurs R de notre statistique: T1, T2, …, TR. Nous les appelons des réalisations bootstrap de T ou une distribution bootstrap de T. Sur cette base, nous pouvons calculer CI pour T. Il existe plusieurs façons de le faire. Prendre des centiles semble être le plus facile.

Bootstrap en action

Utilisons (encore une fois) un ensemble de données iris bien connu. Jetez un oeil à une première rangée:

Supposons que nous voulions trouver CIs pour la médiane Sepal.Length, la médiane Sepal.Width et le coefficient de corrélation de rang de Spearman entre ces deux. Nous utiliserons le package boot de R et une fonction appelée… boot. Pour utiliser sa puissance, nous devons créer une fonction qui calcule nos statistiques à partir de données rééchantillonnées. Il devrait avoir au moins deux arguments : un dataset et un vecteur contenant indices d’éléments d’un ensemble de données qui ont été sélectionnés pour créer un échantillon d’amorçage.

Si nous voulons calculer CIs pour plus d’une statistique à la fois, ourfunction doit les renvoyer sous forme d’un seul vecteur.

Pour notre exemple, cela peut ressembler à ceci:

library(boot)foo <- function(data, indices){ dt<-data c( cor(dt, dt, method='s'), median(dt), median(dt) )}

foo choisit les éléments souhaités (dont les nombres sont stockés dans indices) à partir de data et calcule le coefficient de corrélation des deux premières colonnes (method='s' est utilisé pour choisir le coefficient de rang de Spearman, method='p' résultera avec le coefficient de Pearson) et leurs médianes.

Nous pouvons également ajouter des arguments supplémentaires, par exemple. laissez l’utilisateur choisir le type de coefficient de corrélation odcorrélation:

foo <- function(data, indices, cor.type){ dt<-data c( cor(dt, dt, method=cor.type), median(dt), median(dt) )}

Pour rendre ce tutoriel plus général, j’utiliserai la dernière version de foo.

Maintenant, nous pouvons utiliser la fonction boot. Nous devons lui fournir un nom oddataset, la fonction que nous venons de créer, le nombre de répétitions (R) et tous les arguments supplémentaires de notre fonction (comme cor.type). Ci-dessous, j’utilise set.seed pour la reproductibilité de cet exemple.

set.seed(12345)myBootstrap <- boot(iris, foo, R=1000, cor.type='s')

boot function renvoie un objet de la classe appelée… (oui, vous avez raison !)boot. Il a deux éléments intéressants. $t contient les valeurs R de nos statistiques générées par la procédure d’amorçage (réalisations d’amorçage souvent):

$t0 contient les valeurs de nos statistiques dans l’ensemble de données original, complet:

myBootstrap$t0## -0.1667777 5.8000000 3.0000000

L’impression de l’objet boot sur la console donne des informations supplémentaires:

original est identique à $t0. bias est une différence entre la moyenne des réalisations bootstrap (celles de $t), appelée estimation bootstrap de T et la valeur de l’ensemble de données d’origine (celle de $t0).

colMeans(myBootstrap$t)-myBootstrap$t0## 0.002546391 -0.013350000 0.007900000

std. error est une erreur standard de l’estimation d’amorçage, qui est égaleécart standard des réalisations d’amorçage.

apply(myBootstrap$t,2,sd)## 0.07573983 0.10295571 0.02726414

Différents types de CIS d’amorçage

Avant de commencer avec CI, il vaut toujours la peine de jeter un coup d’œil à la distribution des réalisations d’amorçage. Nous pouvons utiliser la fonction plot, avec index indiquant à laquelle des statistiques calculées dans foo nous souhaitons rechercher. Ici, index=1 est le coefficient de corrélation d’un Spearman entre la longueur et la largeur du sépale, index=2 est une longueur médiane du sépale od et index=3 est une largeur médiane du sépale od.

plot(myBootstrap, index=1)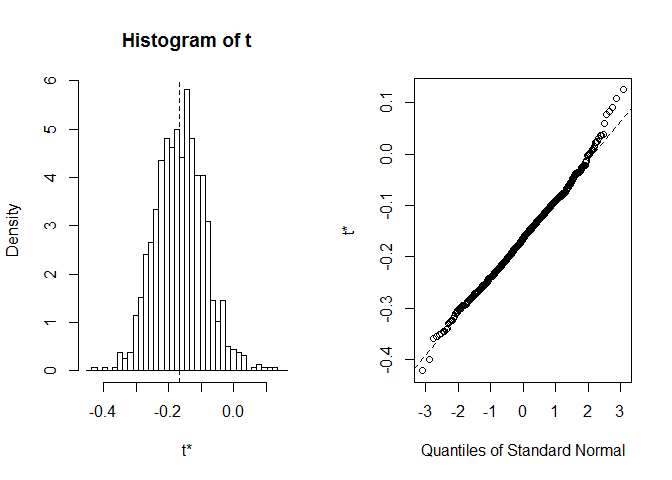

La distribution des coefficients de corrélation de bootstrap semble assezcomme normal. Trouvons CI pour ça. Nous pouvons utiliser boot.ci. Il est par défaut à95% de CIs, mais il peut être modifié avec le paramètre conf.

boot.ci fournit 5 types de CIs bootstrap. L’un d’eux, studentizedinterval, est unique. Il a besoin d’une estimation de la variance d’amorçage. Nous ne le fournissons pas, donc R affiche un avertissement : bootstrap variances needed for studentized intervals. Les estimations de variances peuvent être obtenues avec un bootstrap de deuxième niveau ou (plus facile) avec la technique du couteau. Cela dépasse en quelque sorte le cadre de ce tutoriel, alors concentrons-nous sur les quatre types restants de CIs bootstrap.

Si nous ne voulons pas tous les voir, nous pouvons en choisir des pertinents dans l’argument type. Les valeurs possibles sont norm, basic, stud, perc, bca ouun vecteur de ceux-ci.

La fonction boot.ci crée un objet de classe… (oui, vous l’avez deviné!)bootci. Ses éléments sont appelés comme les types de CI utilisés dans l’argument type. $norm est un vecteur à 3 éléments qui contient le niveau de confiance et les limites CI.

boot.ci(myBootstrap, index=1, type='norm')$norm## conf ## 0.95 -0.3177714 -0.02087672

$basic, $stud, $perc et $bca sont des vecteurs à 5 éléments contenant également des centiles utilisés pour calculer CI (nous y reviendrons plus tard):

boot.ci(myBootstrap, index=1, type='basic')$basic## conf ## 0.95 975.98 25.03 -0.3211981 -0.03285178

Un peu de notation (Désolé!)

Pour avoir une idée de ce que sont les différents types de CI, nous devons introduitcertaines notations. Alors, laissez:

• t⋆ soit l’estimation de bootstrap (moyenne des préétablissements de bootstrap),
• t0 soit une valeur de notre statistique dans l’ensemble de données d’origine,
• se⋆ soit une erreur−type de l’estimation de bootstrap,
• b soit un biais de l’estimation de bootstrapeb =t⋆-t0
• α soit un niveau de confiance, typiquement α = 0,95,
• za soit un $1-\frac\alpha 2$-quantile de la distribution standardnormale,
• θα soit un α-percentile de la distribution des amorçages.

Centile CI

Avec la notation ci-dessus, le centile CI est:

(θ(1-α)/2, θ1-(1-α)/2)

donc, cela ne prend que des centiles pertinents. Rien de plus.

CI normal

Un CI Wald typique serait:

t0 ± za se se⋆

mais dans le cas du bootstrap, nous devrions le corriger pour les biais. Cela devient donc:

t t_0-b \ pm z_\alpha \ cdot se ^\star \ \2t_0-t^\star \ pm z_\alpha \ cdot se^\star

CI de base

Le CI centile n’est généralement pas recommandé car il fonctionne mal lorsqu’il s’agit de distributions à queue bizarre. L’IC de base (également appeléci vectoriel ou empirique) est beaucoup plus robuste à cela. La raison en est de calculer les différences entre chaque réplication bootstrap et t0 et d’utiliser les centiles de leur distribution. Des détails complets peuvent être trouvés, par exemple dans Toutes les statistiques de L. Wasserman

La formule finale pour l’IC de base est:

(2t0-θ1-(1-α) / 2, 2t0-θ(1-α)/2)

BCa CI

BCa provient d’une correction de biais, accélérée. La formulepour ce n’est pas très compliqué mais un peu peu intuitif, alors je vais l’ignorer.Voir l’article de Thomas J. DiCiccio et BradleyEfron si vous êtes intéressé par les détails.

L’accélération mentionnée dans le nom de la méthode nécessite l’utilisation de specificpercentiles de réalisations bootstrap. Parfois, il peut arriver que ce soit des percentiles extrêmes, peut-être des valeurs aberrantes.BCa peut être instable dans de tels cas.

Regardons BCa CI pour la médiane de la largeur des pétales. Dans l’ensemble de données d’origine, cette médiane est précisément égale à 3.

Nous obtenons BCa CI (2.9, 2.9). C’est bizarre, mais heureusement R nous a avertis que extreme order statistics used as endpoints. Voyons ce qui s’est exactement passé ici:

plot(myBootstrap, index=3)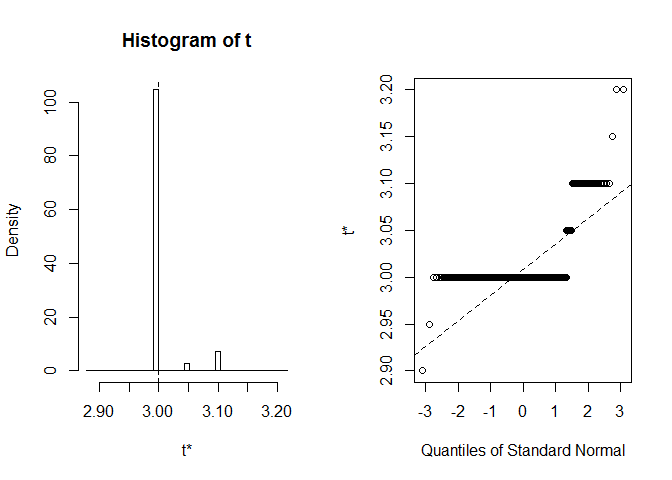

La distribution des réalisations bootstrap est inhabituelle. Une grande majorité d’entre eux (plus de 90%) sont 3s.

table(myBootstrap$t)#### 2.9 2.95 3 3.05 3.1 3.15 3.2## 1 1 908 24 63 1 2

Réplication des résultats

Parfois, nous devons recréer des réplications bootstrap. Si nous pouvons utiliser R pour cela, ce n’est pas un problème. la fonction set.seed résout le problème.Recréer des réplications bootstrap dans d’autres logiciels serait beaucoup plus compliqué. De plus, pour un grand R, le recalcul en R peut également ne pas être une option (par manque de temps, par exemple).

Nous pouvons traiter ce problème en enregistrant des indices d’éléments de l’originaldataset, qui ont formé chaque échantillon d’amorçage. C’est ce que fait la fonction boot.array (avec l’argument indices=T).

tableOfIndices<-boot.array(myBootstrap, indices=T)

Chaque ligne est un échantillon d’amorçage. Par exemple., notre premier échantillon contient les éléments suivants:

Réglage indices=F (par défaut), nous obtiendrons une réponse à la question « Combien de fois chaque élément de l’ensemble de données d’origine est apparu dans chaque échantillon d’amorçage? ». Par exemple, dans le premier échantillon: le 1er élément de l’ensemble de données est apparuune fois, le 2ème élément n’est pas apparu du tout, le 3ème élément est apparu une fois, le 4ème deux fois et ainsi de suite.

Une table comme celle-ci nous permet de recréer la réalisation d’amorçage en dehors de R.Ou dans R lui-même lorsque nous ne voulons pas utiliser set.seed et refaire tout le calcul.

onceAgain<-apply(tableOfIndices, 1, foo, data=iris, cor.type='s')

Vérifions si les résultats sont les mêmes:

Oui, ils le sont!

Si vous souhaitez en savoir plus sur l’apprentissage automatique dans R, suivez le cours Machine Learning Toolbox de DataCamp.