Fondements de l’épidémiologie
Après avoir lu ce chapitre, vous pourrez faire ce qui suit:
- Expliquer ce qu’est la modification de l’effet
- Différencier les facteurs de confusion et les modificateurs d’effet
- Effectuer une analyse stratifiée pour déterminer si une modification de l’effet est présente dans les données
Dans le chapitre précédent, nous avons discuté de la confusion. Un facteur de confusion, vous vous en souviendrez, est une troisième variable qui, si elle n’est pas contrôlée de manière appropriée, conduit à une estimation biaisée de l’association. La modification des effets implique également une troisième variable (pas l’exposition et pas le résultat) – mais dans ce cas, nous ne voulons absolument pas la contrôler. Au contraire, la présence de modification d’effet est en soi une découverte intéressante, et nous la soulignons.
Lorsque la modification de l’effet (également appelée interaction) est présente, il y aura des résultats différents pour différents niveaux de la troisième variable (également appelée covariable). Par exemple, si nous effectuons une étude de cohorte sur la quantité de sommeil et la GPA parmi les étudiants de l’Oregon State University (OSU) au cours d’un trimestre, nous pourrions collecter ces données:
| GPA | |||
| < 3.0 | ≥ 3.0 | ||
| Quantité de Sommeil | < 8 heures | 25 | 25 |
| > 8 heures | 25 | 25 | |
Comme il s’agissait d’une étude de cohorte, nous calculons le ratio de risque (RR):
Il n’y a aucune association entre la quantité de sommeil et la GPA subséquente. À l’aide de la phrase modèle, cela peut être indiqué:
Il s’agit d’un rapport de risque issu d’une étude de cohorte, nous devons donc inclure le délai — ce que j’ai fait en disant « pour terminer le terme ». Tout comme pour la confusion, nous appelons cela le RR non ajusté ou brut.
Cependant, en discutant avec les étudiants, nous nous demandons si le genre pourrait être une covariable importante. Comme pour la confusion, nous effectuerions une analyse stratifiée pour vérifier la modification de l’effet. Encore une fois, nous dessinons des tableaux 2 × 2 avec la même exposition (sommeil) et le même résultat (GPA), mais nous dessinons des tableaux séparés pour les hommes et les femmes (le sexe est la covariable). Pour ce faire, nous examinons les données brutes et déterminons combien des 25 personnes de la cellule A (E +, D +) ci-dessus étaient des hommes et combien étaient des femmes. Supposons que des 25 personnes ayant déclaré < 8 heures et ayant eu une GPA < 3.0, 11 étaient des hommes et 14 étaient des femmes. Nous divisons ensuite de la même manière les participants des cellules B, C et D et créons des tableaux 2 x 2 spécifiques à la strate:
| Hommes | GPA | ||
| < 3.0 | ≥ 3.0 | ||
| Quantité de Sommeil | < 8 heures | 11 | 14 |
| 8+ heures | 17 | 9 | |
| Femmes | GPA | ||
| < 3.0 | ≥ 3.0 | ||
| Quantité de Sommeil | < 8 heures | 14 | 11 |
| 8+ heures | 8 | 16 | |
RRmen =\frac {(\frac{11}{25})}{(\ frac{17}{26})} = 0.68
RRwomen =\frac {(\frac{14}{25})}{(\ frac{8}{24})} = 1.7
Interprétations:
Parmi les étudiants de sexe masculin, ceux qui dormaient moins de 8 heures par nuit avaient 0,68 fois le risque d’avoir une GPA <3.0 à la fin du trimestre, par rapport à ceux qui ont déclaré 8 heures ou plus.
Parmi les étudiantes, celles qui dormaient moins de 8 heures par nuit avaient 1,7 fois plus de risque d’avoir une GPA < 3,0 à la fin du trimestre, par rapport à celles qui déclaraient 8 heures ou plus.
Dormir moins de 8 heures est associé – dans ces données hypothétiques – à une GPA plus élevée chez les étudiants de sexe masculin (le « résultat » est une GPA faible, donc un RR inférieur à 1 indique que les personnes exposées sont moins susceptibles d’avoir une GPA faible) mais avec une GPA plus faible chez les étudiantes.
Le sexe agit dans ce cas comme un modificateur d’effet: l’association entre le sommeil et la GPA varie selon les strates de la covariable. Vous pouvez repérer la modification de l’effet lors de l’analyse stratifiée compte tenu des éléments suivants:
- Les mesures d’association spécifiques à la strate sont différentes les unes des autres
- Le brut se situe entre elles
Si vous avez une modification de l’effet, l’étape suivante consiste à signaler les mesures spécifiques à la strate. Nous ne calculons pas de mesure ajustée (elle serait proche de 1,0, similaire au brut); la chose intéressante ici est que les hommes et les femmes réagissent différemment au sommeil. La modification des effets est quelque chose que nous voulons mettre en évidence dans nos résultats, pas quelque chose à ajuster.
Contrairement à la confusion, où un changement de 10% du brut au corrigé est une définition acceptée pour la confusion, il n’existe pas de définition standardisée de la différence entre les mesures spécifiques à la strate pour appeler quelque chose un modificateur d’effet. Le seuil devrait probablement être plus élevé que celui nécessaire pour déclarer quelque chose comme un facteur de confusion, car une fois que vous déclarez quelque chose comme un modificateur d’effet, vous êtes ensuite obligé de rapporter les résultats séparément pour chaque niveau de la covariable — quelque chose qui réduit votre puissance d’au moins la moitié. Ainsi, en épidémiologie, nous voyons rarement des preuves de modification de l’effet rapportées dans la littérature. Pour faire court, assez « différent » pour la modification des effets est « sans équivoque différent. »
Lors de la lecture d’articles, la modification de l’effet sera parfois appelée interaction, ou les auteurs pourraient simplement dire qu’ils rapportent des analyses stratifiées. L’une de ces 3 phrases est un indice qu’il existe une variable agissant comme modificateur d’effet.
Exemple de modification d’effet II
Suite à la récession de 2008 provoquée par la bulle immobilière (c’est l’exposition), l’économie américaine a perdu beaucoup d’emplois. Voici un graphique montrant le nombre de personnes qui travaillaient (le résultat) avant, pendant et après la récession. Les résultats sont présentés stratifiés par sexe (une covariable), ce qui signifie que l’analyste soupçonnait que le sexe pourrait agir comme un modificateur d’effet. En effet, les résultats sont légèrement différents : les hommes (en bleu) ont perdu une plus grande proportion d’emplois et, en 2014, ils n’avaient pas encore retrouvé leurs niveaux d’avant la récession, tandis que les femmes (en rouge) ont perdu moins d’emplois et, en 2014, elles s’étaient complètement rétablies.

Source: https://fred.stlouisfed.org/graph/fredgraph.png?g=qUs
Et si nous stratifiions aussi par âge? Premièrement, voici un graphique montrant comment la récession a affecté les emplois des personnes âgées de 55 ans et plus:
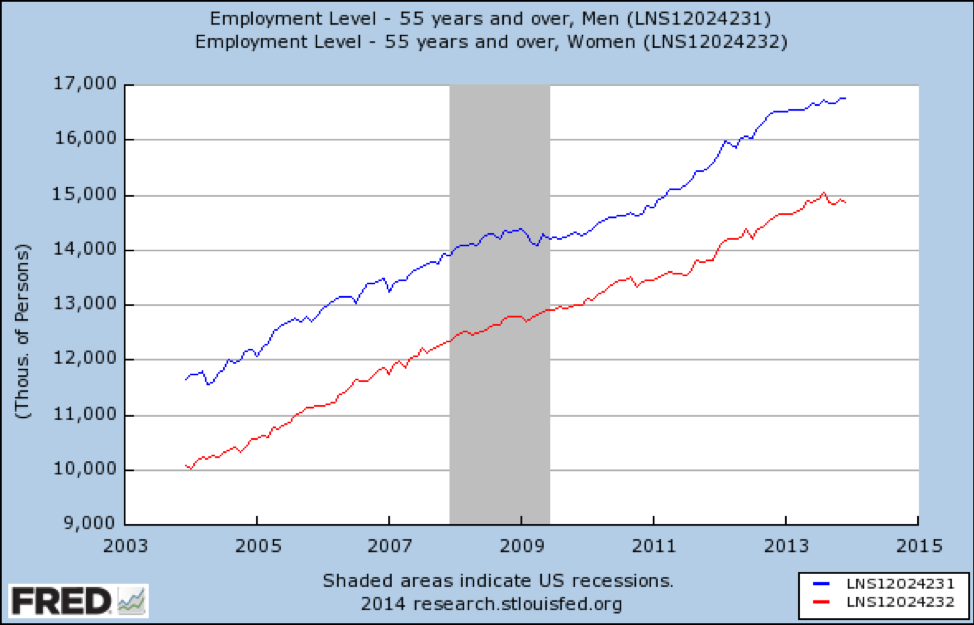
Source: https://fred.stlouisfed.org/graph/fredgraph.png?g=qUt
La récession n’a pas du tout affecté les Américains plus âgés qui travaillent. Nous ne voyons pas non plus de modification de l’effet par sexe — les 2 lignes sont presque parallèles.
Qu’en est-il des jeunes adultes?
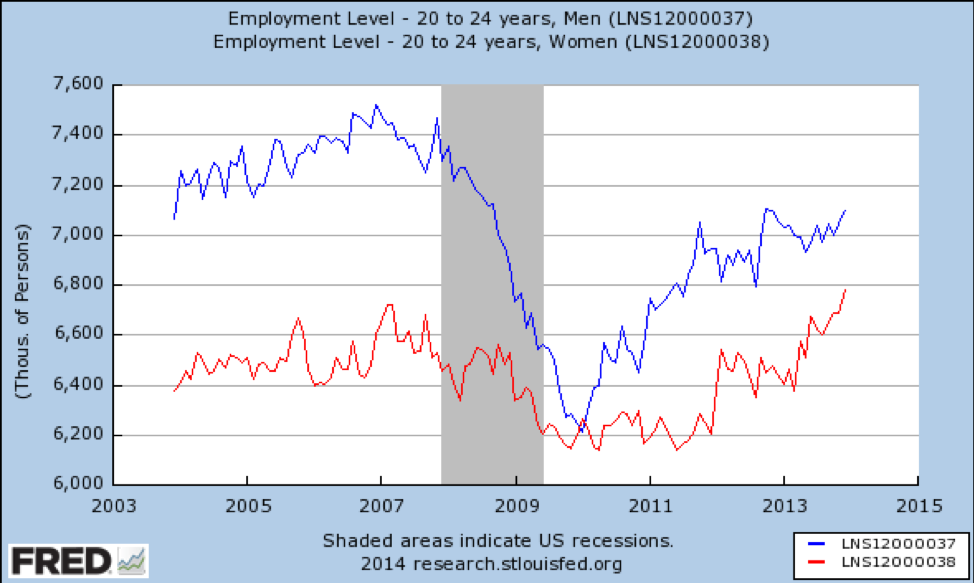
Source: https://fred.stlouisfed.org/graph/fredgraph.png?g=qUv
Ici, nous avons une modification majeure de l’effet selon le sexe — les jeunes hommes ont perdu une grande partie des emplois disponibles et ne s’étaient pas complètement rétablis en 2014. Ce n’est pas surprenant, car la récession a été causée en grande partie par la bulle immobilière et les travailleurs de la construction sont principalement des jeunes hommes. En revanche, les jeunes femmes ont perdu une faible proportion d’emplois et ont rapidement retrouvé des niveaux supérieurs à ceux d’avant la rentrée.
Enfin, nous examinons les emplois pour les 25 à 54 ans:
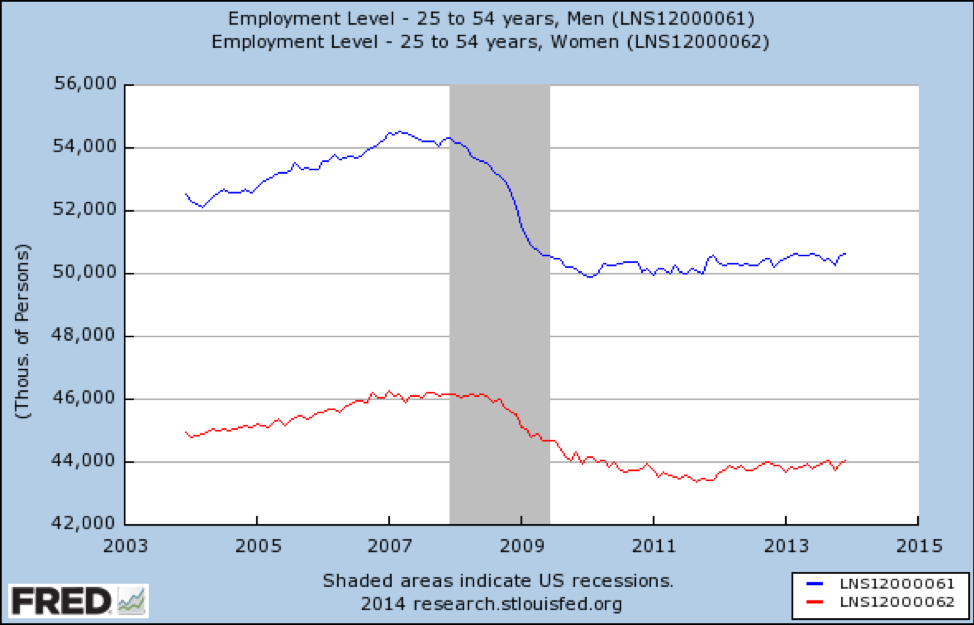
Source: https://fred.stlouisfed.org/graph/?id=LNS12000061
Ici, nous voyons une image très sombre. Dans ce groupe d’âge, les emplois ont été perdus — plus pour les hommes que pour les femmes — et en 2014, ils ne s’étaient pas du tout rétablis.
Ainsi, lors de l’examen de la réponse du marché du travail à la récession de 2008, nous constatons une modification substantielle des effets selon l’âge (la reprise de l’emploi variait considérablement selon l’âge) et, dans certaines catégories d’âge, des preuves de modification des effets selon le sexe. Les effets de la récession sur l’emploi étaient différents pour les personnes d’âges et de sexes différents.
Ceci est important car les implications politiques seraient très différentes. Imaginez que vous travailliez au sein du gouvernement fédéral et que vous essayiez de concevoir un plan de relance ou de relance économique. Si les seules données que vous aviez provenaient du premier graphique, sans les ventilations par âge, les solutions politiques potentielles seraient très différentes de si vous aviez également accès à l’analyse stratifiée par âge.
Avec la confusion, vous obtenez initialement la mauvaise réponse car la confusion n’est pas répartie uniformément entre vos groupes. Cela fausse la mesure d’association que vous calculez (rappelez-vous: avoir des pieds plus gros est associé à la vitesse de lecture uniquement en raison de la confusion par niveau scolaire). Donc, au lieu de cela, vous devez recalculer la mesure d’association, cette fois en ajustant le facteur de confusion.
Avec la modification de l’effet, vous obtenez également initialement la mauvaise réponse, mais cette fois, c’est parce que votre échantillon contient au moins 2 sous-groupes dans lesquels l’association exposition / maladie est différente. Dans ce cas, vous devez séparer en permanence ces sous-groupes et rapporter les résultats (qui peuvent ou non être confondus par d’autres covariables) séparément pour chaque strate: dans ce cas, les hommes qui dorment moins ont des AGP plus élevées que les hommes qui dorment plus, mais en même temps, les femmes qui dorment plus ont des AGP plus élevées que les femmes qui dorment moins.
Voici un tableau récapitulatif indiquant le processus de traitement des facteurs de confusion potentiels et des modificateurs d’effets. Une grande partie du processus est la même quel que soit le type de covariable que vous avez (dans tous les cas, vous devez mesurer la covariable pendant votre étude, et bien la mesurer!). Les zones de différence sont indiquées en rouge.
| Confusion | Modification de l’effet | |
| Avant de planifier une étude | Réfléchissez aux variables qui pourraient servir de facteurs de confusion en fonction de ce que vous savez du processus d’exposition / maladie à l’étude. | Réfléchissez aux variables qui pourraient agir comme modificateurs d’effet en fonction de ce que vous savez du processus d’exposition/maladie à l’étude. |
| Au cours d’une étude | , Collectez des données sur les covariables potentielles — des analyses stratifiées / ajustées ne peuvent être effectuées sans données sur les covariables! | Recueillir des données sur les covariables potentielles — des analyses stratifiées/ajustées ne peuvent être effectuées sans données sur les covariables! |
| Analyse: Étape 1 | Calculez la mesure brute d’association (en ignorant la covariable). | Calculez la mesure brute d’association (en ignorant la covariable). |
| Analyse: Étape 2 | Calculez des mesures d’association spécifiques à la strate, de sorte que chaque niveau de la covariable ait sa propre table 2 x 2. | Calculez des mesures d’association spécifiques à la strate, de sorte que chaque niveau de la covariable possède sa propre table 2 x 2. |
| Analyse: Étape 3 | Si les mesures spécifiques à la strate sont similaires les unes aux autres et au moins 10% différentes du brut (qui ne tombe pas entre elles), alors la covariable est confondante. | Si les mesures spécifiques à la strate sont différentes les unes des autres et que le brut se situe entre elles, alors la covariable est un modificateur d’effet. |
| Les résultats de rédaction | Indiquent une mesure d’association ajustée qui contrôle le facteur de confusion. | Rapportez les mesures d’association spécifiques à la strate. |
Imaginez que vous fassiez une étude transversale de l’activité physique et de la démence chez les personnes âgées et que vous calculiez un rapport de cotes (RO) non ajusté de 2,0. Vous pensez que l’état matrimonial pourrait être une covariable importante, vous stratifiez donc par « actuellement marié » par rapport à « pas actuellement marié » (ce qui inclut jamais marié, divorcé et veuf). La OU parmi les personnes actuellement mariées est de 3,1, et parmi les personnes non actuellement mariées, la OU est de 3,24. Dans ce cas, l’état matrimonial agit comme un facteur de confusion, et nous rapporterions le OU ajusté (qui serait de 3,18 environ).
Imaginez que vous fassiez un essai randomisé d’un régime méditerranéen pour prévenir les naissances prématurées chez les femmes enceintes. Vous faites l’essai et calculez un RR de 0,90. Vous pensez que la parité pourrait peut-être être une covariable importante, alors vous effectuez une analyse stratifiée. Parmi les nulliparas, le RR est de 0,60 et parmi les multiparas, le RR est de 1,15. Ceux-ci sont différents les uns des autres, et le brut se trouve entre eux. Dans ce cas, la parité agit comme un modificateur d’effet, et vous devez donc signaler les 2 RR spécifiques à la strate séparément.
Imaginez que vous fassiez une étude cas-témoins du mélanome et de l’utilisation antérieure d’un lit de bronzage. Le brut OU est de 3,5, mais le genre est peut-être une covariable importante. L’analyse stratifiée donne un OU de 3,45 chez les hommes et de 3,56 chez les femmes. Dans ce cas, la covariable (genre) n’est ni un facteur de confusion ni un modificateur d’effet. Nous disons qu’il ne s’agit pas d’une confusion car (1) le brut se situe entre les 2 estimations spécifiques à la strate, mais aussi (2) les estimations spécifiques à la strate ne diffèrent pas de plus de 10% du brut. Nous disons que ce n’est pas un modificateur d’effet car 3,45 et 3,56 ne sont pas si différents — dans les deux cas, il y a un effet substantiel (environ 3,5 fois plus élevé). Nous rapporterions l’estimation grossière de l’association, car elle ne nécessite ni ajustement ni stratification pour tenir compte des effets du genre.
Oui ! Habituellement, nous le voyons lorsque la covariable en question est une variable continue, dichotomisée dans le but de vérifier la modification de l’effet. Par exemple, si nous pensons que l’âge pourrait être un modificateur d’effet, nous pourrions diviser notre échantillon en « vieux » et « jeune » pour l’analyse stratifiée — disons, plus de 50 ans contre 50 ans ou moins. Dans la mesure où les 51 ans ne sont pas comme les 70 ans, nous pourrions manquer certaines nuances importantes dans les résultats, peut-être parce qu’il existe dans les données une modification supplémentaire des effets avec plus de catégories (ce qui réduirait le pouvoir à presque rien, si nous devions rendre compte séparément des strates supplémentaires) ou une confusion « résiduelle » comme discuté dans le chapitre précédent. D’autres détails dépassent le cadre de ce livre, mais sachez que la même covariable peut théoriquement agir à la fois comme un facteur de confusion et un modificateur d’effet — mais que l’on voit rarement cela dans la pratique.
Conclusion
Contrairement à la confusion, dont nous voulons éliminer les effets dans notre analyse, la modification des effets est une découverte intéressante en soi, et nous la rapportons. Pour vérifier la modification de l’effet, effectuez une analyse stratifiée. Si les mesures d’association spécifiques à la strate sont différentes les unes des autres et que le brut se situe entre elles, il est probable que la variable en question agisse comme un modificateur d’effet. Rapportez les résultats séparément pour chaque strate de la covariable.
Une table finale, mise-tout-ensemble:
| Si ce sont vos SRO/RR: | ||||
| Brut/Non ajusté | Strate | Strate | Alors la covariable est… | Et vous rapporteriez… |
| 2.0 | 1.0 | 3.2 | un modificateur d’effet | les 2 mesures d’association spécifiques à la strate |
| 2.0 | 3.5 | 3.6 | un facteur de confusion | une mesure ajustée |
| 2.0 | 1.9 | 2.0 | rien d’intéressant | la mesure brute |
Une erreur systématique dans une étude (certaines personnes appellent cela un biais; je préfère ne pas le faire) qui est causée par une troisième variable interférant dans la relation exposition-maladie.
Fait référence au scénario où la relation entre une exposition et un résultat varie sur la base d’une troisième variable. Par exemple, peut-être que le yoga prévient les blessures au LCA chez les femmes mais pas chez les hommes. Le sexe dans ce scénario est le modificateur d’effet. La modification de l’effet n’est pas la même chose que la confusion.
La probabilité que votre étude trouve quelque chose qui est là. Puissance = 1-β ; beta est le taux d’erreur de type II. Les petites études, ou études d’événements rares, sont généralement sous-alimentées.
Combien d’enfants une femme a eu. Les femmes nullipares (aka nulliparas) n’ont pas encore eu leur premier enfant (elles peuvent être enceintes, mais n’ont pas encore eu d’enfant), et les femmes parous ont eu au moins un enfant précédent. Les multiparas ont eu au moins deux enfants précédents; les primiparas ont eu un enfant précédent.
C’est la première grossesse d’une femme.
Cette femme a eu d’autres enfants.