KDnuggets

Par Sydney Firmin, Alteryx.

 » Essentiellement, tous les modèles sont faux, mais certains modèles sont utiles. »- George Box

Cette célèbre citation de George Box a été enregistrée pour la première fois en 1976 dans l’article « Science and Statistics », publié dans le Journal of the American Statistical Association. C’est une citation importante dans le domaine des statistiques et des modèles analytiques et peut être décomposée en deux parties.

Tous les modèles se trompent

Pour approfondir cette déclaration, nous devons définir et examiner ce qu’est un modèle.

Pour le contexte de cet article, un modèle peut être considéré comme une représentation simplifiée d’un système ou d’un objet. Les modèles statistiques rapprochent les modèles d’un ensemble de données en faisant des hypothèses sur les données ainsi que sur l’environnement dans lequel elles ont été recueillies et appliquées.

Les trois grandes catégories d’hypothèses formulées par les modèles statistiques sont les hypothèses de répartition (hypothèses sur la distribution des valeurs dans une variable ou la distribution des erreurs d’observation), les hypothèses structurelles (hypothèses sur la relation fonctionnelle entre les variables) et les hypothèses de variation croisée (distribution de probabilité conjointe).

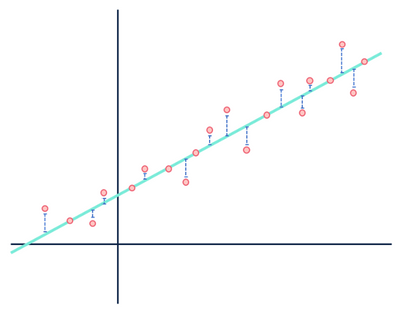
Par exemple, un modèle de régression linéaire suppose que les relations entre les variables d’un ensemble de données sont linéaires (et seulement linéaires). Aux yeux d’un modèle linéaire, toute distance entre les observations qui composent l’ensemble de données et la ligne modélisée n’est que du bruit (c’est-à-dire des fluctuations aléatoires ou inexpliquées des données) et peut finalement être ignorée.

Ne vous souciez pas des distances en bleu.

George Box a déclaré que tous les modèles sont erronés, en particulier dans le contexte des modèles statistiques. Parce que la nature même d’un modèle est une représentation simplifiée et idéalisée de quelque chose, tous les modèles seront faux dans un certain sens. Les modèles ne seront jamais « la vérité » si la vérité signifie entièrement représentative de la réalité. Il est très important de tenir compte des hypothèses formulées lors de la génération d’un modèle, car les modèles ne sont vraiment utiles que lorsque les hypothèses sont maintenues.

Cartes et miniatures

Des observations similaires à « tous les modèles sont faux » de Box sont présentes dans de nombreux domaines différents.

Il existe un aphorisme qui fait référence à la relation carte-territoire, attribuée à Alfred Korzybski:

Une carte n’est pas le territoire qu’elle représente, mais, si elle est correcte, elle a une structure similaire au territoire, ce qui explique son utilité.

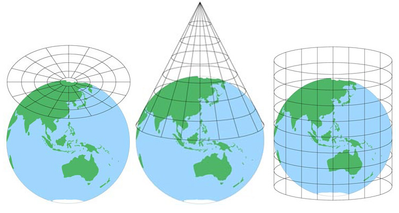
Les cartes sont utiles car ce sont des abstractions d’un objet réel à une échelle plus gérable, mais elles excluront toujours un certain niveau de détail. Selon la superficie d’une carte, il peut également y avoir une certaine distorsion due à la projection de la carte (causée par le processus délicat de conversion d’un globe sphérique en une représentation plate).

( Source de l’image.)

La seule carte vraiment précise serait une réplication 1:1 du territoire qu’elle représente. Cependant, une carte comme celle-ci ne serait pas plus utile que de naviguer sur le territoire lui-même.

Considérons la citation du poète Paul Valéry:

Tout ce qui est simple est faux. Tout ce qui est complexe est inutilisable.

Nommé d’après un professeur de commerce de Stanford, le paradoxe de Bonini décrit le défi de créer des modèles ou des simulations utiles et complets de systèmes complexes. Il y a souvent un équilibre entre la complexité et la précision dans le développement de modèles. Si l’objectif d’un modèle est de rendre une relation ou un système plus clair, une complexité accrue va à l’encontre de cet objectif (bien que cela puisse rendre le modèle plus précis).

À un niveau élevé, la relation carte-territoire décrit également la relation entre un objet et une représentation de l’objet.

Si vous avez déjà suivi un cours de philosophie, vous êtes peut-être tombé sur l’œuvre La Trahison des Images de l’artiste surréaliste René Magritte.

Le texte se traduit par « Ce n’est pas un tuyau. » Et ce n’est pas le cas. Nous ne pouvons pas bourrer cette image (numérique) de tabac et la fumer car ce n’est qu’une représentation d’un objet réel.

Les modèles sont des abstractions. Comme les cartes, ou les modèles architecturaux miniatures, ou les schémas, ils ne peuvent pas capturer tous les détails de l’objet ou du système sur lequel ils sont basés, ne serait-ce que parce qu’ils n’existent pas dans le monde réel et ne fonctionnent pas de la même manière.

Si Tous Les Modèles Sont Faux, Pourquoi S’Embêter?

L’aphorisme de George Box n’est pas sans ses critiques.

Le problème que rencontrent de nombreux statisticiens avec cette citation semble se diviser en deux catégories:

1. Les modèles se trompent est une déclaration évidente. Bien sûr, tous les modèles sont faux, ce sont des modèles.
2. Cette citation est utilisée comme excuse pour les mauvais modèles.

Le statisticien J. Michael Steele a critiqué l’adage (voir cet essai personnel). L’argument principal de Steele est que  » faux  » n’entre en jeu que si le modèle ne répond pas correctement à la question à laquelle il prétend répondre (p. ex., qu’un bâtiment sur une carte est mal étiqueté, pas que le bâtiment soit représenté par un petit carré). Steele poursuit en déclarant:

La majorité des méthodes statistiques publiées ont faim d’un exemple honnête.

Steele soutient que les modèles statistiques ne sont souvent pas à la hauteur d’une mesure adéquate de la condition physique et que de nombreux modèles développés par les statisticiens ne sont pas suffisants pour les cas d’utilisation prévus.

Dans l’article La statistique comme une science, pas un Art: La façon de survivre dans la science des données, Mark van der Laan (Statistics at UC Berkeley) attribue la citation de la boîte comme une cause contributive de mauvais modèles statistiques et la rejette comme « un non-sens complet. » Il continue à écrire:

Le fondement de la statistique (…) n’aurait pas pu être de choisir arbitrairement un modèle statistique « pratique « . Cependant, c’est précisément ce que font allègrement la plupart des statisticiens, se référant fièrement à la citation: « Tous les modèles sont faux, mais certains sont utiles. »Pour cette raison, les modèles si irréalistes qu’ils sont indexés par un paramètre de dimension finie restent le statu quo, même si tout le monde convient qu’ils sont connus pour être faux.

En guise de solution, Van der Laan appelle les statisticiens à cesser d’utiliser la citation de Box et à s’engager à prendre au sérieux les données, les statistiques et la méthode scientifique. Il appelle les statisticiens à passer du temps à apprendre comment les données d’un ensemble de données donné ont été générées et à s’engager à développer des modèles statistiques réalistes utilisant l’apprentissage automatique et des techniques d’estimation adaptatives aux données par rapport aux modèles paramétriques plus traditionnels.

Cet article contient les réponses des statisticiens Michael Lavine et Christopher Tong, ainsi qu’une réponse aux réponses de l’auteur original. Les deux statisticiens réfuteurs citent des exemples où les modèles sont connus pour être erronés, mais sont souvent utilisés parce qu’ils sont utiles et adaptés à un problème donné. Leurs exemples incluent les trois modèles de lumière différents trouvés dans le domaine de l’optique (optique géométrique, optique physique et optique quantique; les trois modèles représentent la lumière différemment, sont « faux » dans un certain sens et sont encore utilisés aujourd’hui), et la relation (presque) linéaire entre le journal du flux de carbone et la température du sol trouvée dans les données collectées dans la forêt de Harvard.

À son tour, Van der Laan répond à ces exemples et à d’autres critiques de son article, en particulier à son concept de trouver un « vrai » modèle. Les lettres de réponse valent vraiment la peine d’être lues si vous êtes intéressé. Cela représente un domaine de débat actif dans les domaines de la statistique et de la science des données.

Mais Certains Modèles Sont utiles

Malgré les limitations des modèles, de nombreux modèles peuvent être très utiles. Parce qu’ils sont simplifiés, les modèles sont souvent utiles pour comprendre un certain composant ou une certaine facette d’un système.

Dans le contexte de la science des données, l’apprentissage automatique et les modèles statistiques peuvent être utiles pour estimer (prédire) des valeurs inconnues. Dans de nombreux contextes, si les hypothèses du modèle se maintiennent, une estimation incertaine fournie par un modèle statistique solide peut encore être très utile pour prendre des décisions.

La deuxième moitié moins citée de la sagesse de George Box est la suivante:

 » La question pratique est de savoir à quel point les modèles doivent être erronés pour ne pas être utiles. » – George Box

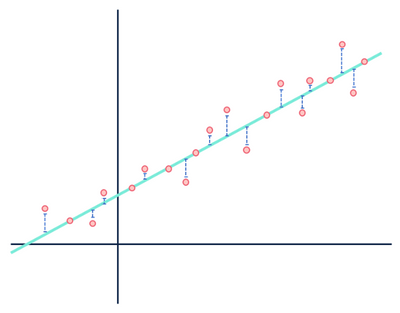
Jetons un autre coup d’œil à notre exemple de régression linéaire:

La plupart du temps, j’ai passé trop de temps sur cette image pour l’utiliser une seule fois.

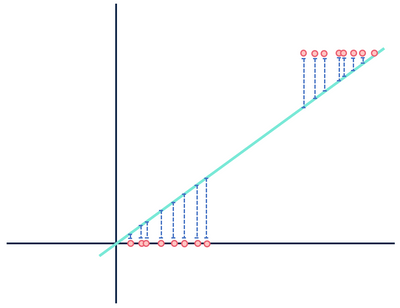
Examinons maintenant un autre modèle de régression linéaire théorique adapté à un ensemble de données différent.

Ne vous souciez pas des distances wait attendez, ça ne peut pas être juste.

Les deux chiffres montrent une erreur, mais un ensemble de données démontre une relation clairement linéaire tandis que l’autre est logistique. Les deux modèles sont « faux », mais l’un capture clairement une relation réelle entre les variables, tandis que l’autre ne le fait pas, rendant l’un utile et l’autre inutile. L’élimination des distances en bleu en tant que bruit est raisonnable si les données ont une relation linéaire, mais cette hypothèse s’effondre lorsque la relation a une forme fonctionnelle différente de celle du modèle sélectionné.

Faire de bons modèles

Le fait que les modèles soient faux ou limités dans la portée de ce qu’ils représentent peut sembler évident pour beaucoup de gens qui travaillent avec des modèles, mais malheureusement, beaucoup de gens ne s’en rendent pas compte ou n’y pensent pas beaucoup. C’est pourquoi je pense qu’il est important de garder les mots de George Box à l’esprit lors de l’élaboration d’un modèle. Il ne devrait pas être utilisé comme excuse pour construire de mauvais modèles.

Pour en savoir plus, Steele a de bonnes notes de classe: Le Modèle A-t-il un sens? et le Modèle A-T-Il Un Sens? Partie II: Exploiter la suffisance. Une autre excellente ressource est l’article « Tous les modèles se trompent… »: une introduction à l’incertitude des modèles lors d’un atelier de sélection de modèles tenu en 2011 à Groningue.

Une autre lecture intéressante est Quand Tous les modèles se trompent des questions de Science et de technologie, ce qui fait appel aux mots de Box comme un appel à une transparence plus stricte dans les modèles scientifiques et statistiques.

L’important à retenir de tout cela est de vous assurer de comprendre quels aspects de vos données sont capturés par votre modèle et quels aspects ne le sont pas. Il est essentiel de vérifier vos hypothèses et vos points de départ. En tant que statisticien ou data scientist, il est de votre responsabilité de produire des modèles rigoureux et de connaître leurs limites. Signalez toujours votre incertitude ainsi que la portée de votre modèle. Dans cet esprit, vous pourrez créer des modèles qui, bien que peut-être faux, peuvent certainement être utiles.

Original. Republié avec permission.

Bio: Géographe de formation et geek des données dans l’âme, Sydney croit fermement que les données et les connaissances sont les plus précieuses lorsqu’elles peuvent être clairement communiquées et comprises. Dans son rôle actuel d’ingénieure de contenu en Science des données, elle passe ses journées à faire ce qu’elle aime le plus: transformer les connaissances techniques et la recherche en contenu engageant, créatif et amusant pour la communauté Alteryx.

Liés:

• Les 3 Plus grandes Erreurs d’Apprentissage de la Science des Données
• 3 Gros Problèmes avec le Big Data et Comment Les Résoudre
• Choisir Entre des Modèles Candidats