Le système solaire: La Terre et la Lune
Les planètes sont à des dizaines et des centaines de millions de kilomètres de nous. Pour éviter l’utilisation de nombres aussi importants, l’Unité astronomique (UA) est adoptée comme unité de distance, c’est-à-dire la distance moyenne entre la Terre et le Soleil, 149 600 000 km.La lumière prend 8 minutes et 19 secondes pour couvrir cette distance.
La taille du Système solaire dépasse l’orbite de Pluton à 40 UA et est définie comme celle dans laquelle la force d’attraction du Soleil est égale à la force d’attraction des étoiles les plus proches de nous. Les dimensions du système solaire seraient alors de l’ordre de 1,5 105 UA. Évidemment, ces dimensions sont très petites par rapport aux dimensions de la galaxie ou de l’Univers visible. Les unités prises pour mesurer ces distances énormes sont l’année-lumière et le parsec qui équivaut à 206 265 UA ou 3,26 années-lumière.
Les planètes du Système solaire sont divisées en deux groupes: le groupe terrestre formé par Mercure, Vénus, la Terre et Mars et le groupe des planètes géantes formé par Jupiter, Saturne, Uranus et Neptune.
Toutes les planètes sauf Vénus et Mercure ont des satellites, dont la plupart appartiennent aux planètes géantes. La Terre, Jupiter, Saturne et Neptune ont les plus gros satellites: la Lune, les satellites de Jupiter découverts par Galilée (Io, Europa, Ganymède, Callisto), le satellite Titan de Saturne et Triton de Neptune.
Les astéroïdes occupent une vaste région annulaire entre les orbites de Mars et de Jupiter, à une distance moyenne de 2,75 UA du Soleil. Le plus grand astéroïde est Cérès qui a un diamètre de 1000 km.
Les comètes, qui ont été cataloguées environ 600, sont divisées en deux groupes, à courte période (moins de 20 ans) et à longue période (plus de 20 ans). Il existe plusieurs hypothèses sur l’origine des comètes, dont celle de l’astronome néerlandais J. Oort.
En plus des corps mentionnés dans l’espace interplanétaire, il existe un grand nombre de particules de tailles différentes, principalement celles d’une masse de millièmes ou de millionièmes de gramme, appelées poussières météoriques. La formation de ces particules est probablement due à la collision de corps plus gros (astéroïdes) et à leur fragmentation successive tout au long de l’existence et de l’évolution du Système solaire.
La poussière météorique est responsable du phénomène de lumière zodiacale, qui s’observe après le crépuscule ou avant l’aube, en raison de la dispersion de la lumière par ces particules de poussière. La plupart des particules s’évaporent en entrant dans l’atmosphère terrestre (à des altitudes comprises entre 80 et 120 km), seule une faible proportion atteignant la surface de la terre.
regardons maintenant quelques données relatives aux planètes du Système solaire
Premier du Soleil
| masse du corps céleste | Radio | |
|---|---|---|
| Soleil | 6,96 * 108 m | 1,98 * 1030 kg |
Puis, hors de la Terre
| corps céleste | demi-grand axe | Période | Masse |
|---|---|---|---|
| Terre | 149,6 * 109 m | 1 an = 365,26 jours | 5.98 · 1024 kg |
et le reste des planètes
| Planète | demi-grand axe (AU) | Excentricité | Période (années) | Masse |
|---|---|---|---|---|
| Mercure | 0.387 | 0.206 | 0.24 | 0.06 |
| Vénus | 0.723 | 0.007 | 0.62 | 0.82 |
| Terre | 1.000 | 0.017 | 1.00 | 1.00 |
| Mars | 1.524 | 0.093 | 1.88 | 0.11 |
| Jupiter | 5.203 | 0.048 | 11.86 | 318 |
| Saturne | 9.539 | 0.056 | 29.46 | 95.1 |
| Uranus | 19.182 | 0.047 | 84.01 | 14.6 |
| Neptune | 30.058 | 0.009 | 164.8 | 17.2 |
Dans le tableau suivant sont fournis comme données supplémentaires:
- L’inclinaison du plan de l’orbite de la planète par rapport à l’écliptique (plan de l’orbite de la Terre)
- La période de rotation autour de son axe. Il a été très difficile de mesurer cette magnitude pour des planètes comme Mercure et Vénus. Les coquilles gazeuses de Jupiter, Saturne, Uranus et Neptune possèdent la propriété de rotation différentielle, c’est-à-dire que leurs périodes de rotation varient en fonction de la latitude.
- L’inclinaison de l’axe de rotation par rapport au plan de l’orbite. Dans le cas de Vénus, il est de 177º ce qui équivaut à dire que l’inclinaison de l’axe est de 3º mais que le sens de rotation est inverse. Le même argument s’applique à Uranus, ce qui indique que l’axe de rotation d’Uranus est presque dans le plan de son orbite.
| Planète | Inclinaison de l’orbite | Période de rotation | Densité g/cm3 | Équateur radio (km) | inclinaison de l’axe | No. des satellites |
|---|---|---|---|---|---|---|
| Mercure | 7e.0 | 58d.6 | 5.44 | 2 439 | < 30º | 0 |
| Vénus | 3ème.4 | 243d | 5.24 | 6 051 | 177 ° | 0 |
| Terre | 0 | 23 heures.9 | 5.52 | 6 378 | le 23.5 | 1 |
| Mars | 1er.8 | 24h.6 | 3.95 | 3 394 | 25º.2 | 2 |
| Jupiter | 1er.3 | 9h.9 | 1.33 | 71 398 | 3ème.1 | 16 |
| Saturne | 2ème.5 | 10h.2 | 0.69 | 60 000 | 26º.4 | 17 |
| Uranus | 0º.8 | 10h.8 | 1.26 | 25 400 | 98º | 5 |
| Neptune | 1er.8 | 15h.8 | 1.67 | 24 750 | 29º | 2 |
Satellites
Enfin, nous fournissons quelques données concernant les principaux satellites des planètes. Jupiter et Saturne ont de nombreux satellites beaucoup plus gros que ceux de Mars, mais nous ne mentionnons que ceux de taille similaire ou plus grande que notre Lune.
| Planète | Satellites | Densité g/cm3 | Rayon moyen (km) | Orbite radio (103 km) | Période (jours) |
|---|---|---|---|---|---|
| Terre | Lune | 3.33 | 1 738 | 384.4 | 27.32 |
| Mars | Phobos | 2.1 | 13.5 | 9.38 | 0.319 |
| Deimos | 2.1 | 7.5 | 23.46 | 1.262 | |
| Jupiter | Io | 3.53 | 1 820 | 421.6 | 1.769 |
| Europe | 3.03 | 1 565 | 670.9 | 3.551 | |
| Ganymède | 1.93 | 2 638 | 1 070 | 7.155 | |
| Calisto | 1.83 | 2 410 | 1 880 | 16.689 | |
| Saturne | Titan | 1.9 | 2 575 | 1 221.9 | 15.95 |
| Neptune | Triton | 2 200 | 394.7 | 5.84 |
Activités
- Déterminer la masse de la planète Jupiter à partir des données radio et de la période de révolution de l’un de ses satellites.
- Déterminer le rayon de l’orbite d’un satellite de la planète Jupiter à partir de la masse de cette planète et de la période de révolution du satellite.
- Déterminer l’intensité du champ gravitationnel g à la surface des planètes et de certains satellites, à partir des données de leur masse M et de leur rayon R ou de leur densité ρ et de leur rayon.
Exemple : déterminer la masse de la planète Jupiter en sachant que le rayon de l’orbite d’Io est de 421 600 km et que sa période de révolution est de 1 769 jours. Fait: la constante G est de 6,67 * 10-11 Nm2 / kg2
Exemple: Calculez le rayon de l’orbite du satellite Callisto en sachant que sa période de révolution est de 16,689 jours et que la masse de la planète Jupiter est de 1,901 · 1027 kg. Données: la constante G est de 6,67 * 10-11 Nm2/ kg2
g = G M R 2 = 4π 3 GpR
Données : la constante G est 6.67 * 10-11 Nm2 / kg2
La Lune
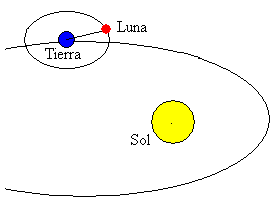
La Lune est l’un des plus grands corps du système solaire. Son orbite est presque circulaire (excentricité ε = 0,05) et le plan de son orbite est incliné de 5º par rapport au plan de l’orbite terrestre.
La distance moyenne entre le centre de la Terre et la Lune est de 384 400 km.Sa période de rotation autour de la Terre est de 27 322 jours. Le changement de position de la Lune par rapport au Soleil donne naissance aux phases de la Lune.
La Lune présente toujours la même face à l’observateur terrestre, en raison de l’effet des forces de marée que la Terre exerce sur la Lune. Ce qui signifie que la période de rotation de la Lune autour de son axe coïncide avec le temps nécessaire pour compléter une orbite autour de la Terre.
La Lune est l’objet céleste qui a le plus fasciné l’espèce humaine. L’ex-Union soviétique a d’abord envoyé un navire automatique qui a atterri à la surface de la Lune en 1959. Le 20 juillet 1969, Neil Armstrong accompagné d’Edwin Aldrin sont les premiers hommes à marcher à la surface de la Lune dans le cadre de la mission Apollo 11. La dernière visite d’astronautes américains sur la Lune a eu lieu en 1972.
L’origine de la Lune semble incertaine, il existe plusieurs théories:
-
il a été formé en même temps que la Terre avec le matériau d’une nébuleuse
-
un corps céleste est divisé en deux parties, donnant naissance à la Terre et à la Lune
-
Que la Lune s’est formée ailleurs et a été capturée par la Terre
-
Que la Terre est entrée en collision avec un objet céleste de grande taille (environ la taille de Mars ou plus), et que la Lune s’est formée avec le matériau expulsé de cette collision.
Cette dernière théorie semble, pour le moment, la plus acceptée par la communauté scientifique.
Chemin de la Lune
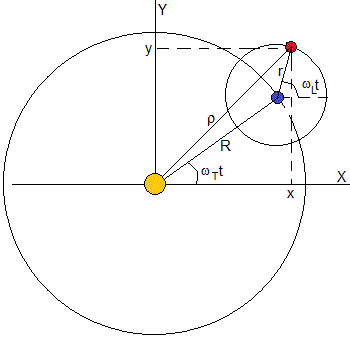
Considérons une planète et son satellite. La planète décrit une orbite circulaire de rayon R autour de son étoile avec une vitesse angulaire constante wT = 2π / PT, PT étant la période ou le temps qui conduit à un tour complet. Le satellite décrit une coplanaire d’orbite circulaire de rayon r à vitesse angulaire constante wL = 2π/PL, étant PL la période ou le temps nécessaire pour effectuer une révolution complète
la position du satellite par rapport à un système de référence dont l’origine est l’étoile, est
x = Rcos(ω T) + rcos(ω L t) y = Risiko (ω T) + risiko (ω L t)
Est α = wT/ wL
{ x = Rcos (α ω L t) + rcos (ω L t) y = Risiko (α ω L t) + risiko (ω L t) { x = Rcos (α 2π P L t) + rcos (2π P L t) y = Risiko (α 2π P L t) + risiko (2π P L t)
nous appellerons τ = t/PL
x R = cos(α·2πτ) + r R cos(2πτ) et R = sin(α·2πτ) + r r sin(2πτ)
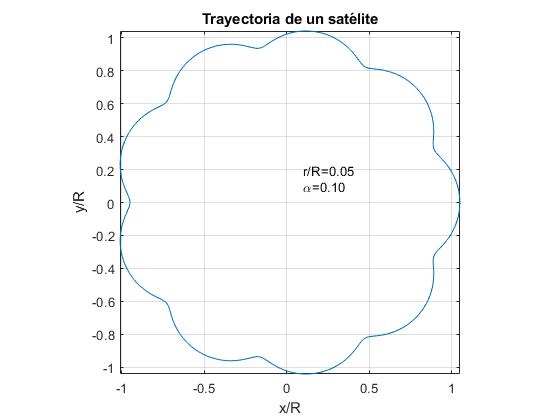
nous représentons la trajectoire d’un satellite pour α = 0,1 et pour trois valeurs du rapport r/R.
- r/R < α. Exemple, r/R = 0,05
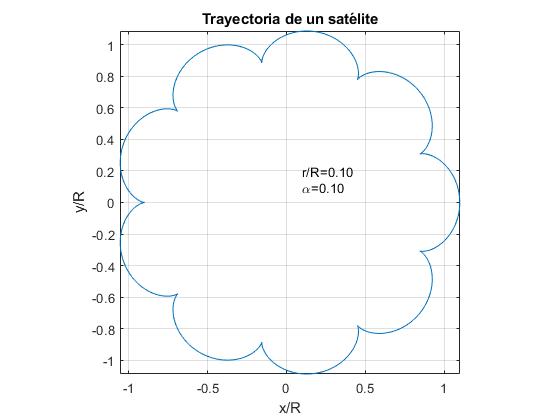
- r/R = α. Exemple, r/R = 0,1
- r/R > α. Exemple, r/R=0.15
alfa=0.1;r=0.15;fplot(@(t) r*cos(2*pi*t)+cos(2*pi*alfa*t), @(t) r*sin(2*pi*t)+sin(2*pi*alfa*t),)text(0.1,0.1,sprintf('\alpha=%1.2f',alfa))text(0.1,0.2,sprintf('r/R=%1.2f',r))axis equalgrid onxlabel('x/R')ylabel('y/R')title('Trayectoria de un satélite')
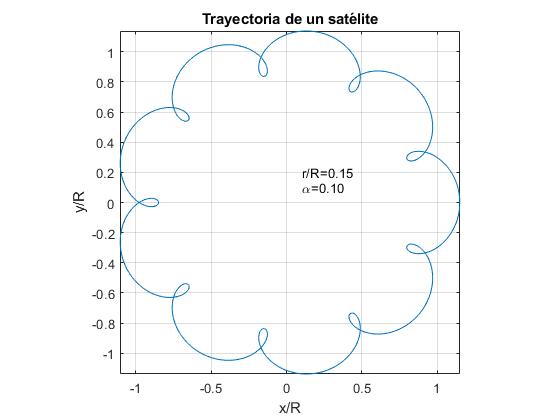
Pour le cas de la Terre et de la Lune, les données sont:
- rayon de l’orbite lunaire : r = 384,4 * 106 m, période PL = 27,32 d
- rayon de l’orbite terrestre: R = 149,6 * 109 m, période PT = 365,26 d
α = POIDS / poids = PL / PT = 0,0748. r / R = 0,0026
L’orbite de la Lune ressemblera au premier chiffre. Dans la représentation graphique de la trajectoire de la Lune pour ces valeurs de α et r/R n’apprécie pas les oscillations de la distance radiale entre le Soleil et la Lune
Accélération de la Lune
La distance ρ du Soleil à la Lune, est
ρ 2 = x 2 + y 2 = R 2 + r 2 + 2rRcos ((ω L−ω T) t)
on calcule les composantes rectangulaires de l’accélération
{ dx dt = − ω T Risiko (ω T) − ω L risiko (ω L t) dy dt = ω T Rco (ω T) + ω L rco (ω L t) { a x = d 2 x d t 2 = − ω T 2 Rco (ω T) − ω L 2 rco (ω L t) y = d 2 y d t 2 = − ω T 2 Risiko (ω T) − ω L 2 risiko (ω L t)
la composante radiale de l’accélération
à ρ = a → · ρ → ρ = a x x + a y x 2 + y 2 = − ω T 2 R 2 + ω L 2 r 2 + (ω T 2 + ω L 2) Rrcos ((ω L−ω T) t) R 2 + r 2 + 2 rr cos ((ω L−ω T) t)
Les valeurs minimale et maximale sont obtenues lorsque cos((wL-wT)t)=±1
a max = – ω T 2 R 2 + ω L 2 r 2 + (ω T 2 + ω L 2) Rr R 2 + r 2 + 2 rr = − (ω T 2 R + ω L 2 r) min = − ω T 2 R 2 + ω L 2 r 2 − (ω T 2 + ω L 2) Rr R 2 + r 2 -2 rr = – (ω T 2 R – ω L 2 r )
>> R=149.6e9; %Tierra>> r=384.4e3; %Luna>> wT=2*pi/(365*24*60*60) %velocidad angular TierrawT = 1.9924e-07>> wL=2*pi/(27.32*24*60*60) %velocidad angular TierrawL = 2.6619e-06>> aM=-(wT^2*R+wL^2*r)aM = -0.0059>> am=-(wT^2*R-wL^2*r)am = -0.0059
La Lune est le seul satellite du Système Solaire, dont la composante radiale de l’accélération est négative, on dit que « la Lune tombe vers le Soleil »,
phases de la Lune
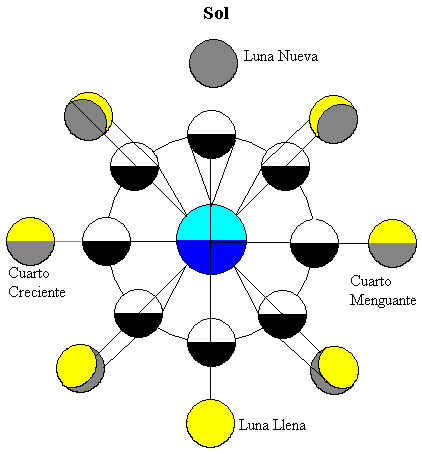
La figure montre la Lune dans différentes positions de son orbite autour de la Terre. Le Soleil est loin d’éclairer les deux corps célestes (en haut de la figure)
La moitié de la Lune est éclairée par le Soleil (en couleur blanche) et la moitié de la Lune la plus proche de la Terre est visible par l’observateur terrestre. Lorsque la Lune se déplace autour de la Terre, nous voyons différentes fractions de la partie éclairée par le Soleil (les zones jaunes).
-
Lorsque la Lune est entre la Terre et le Soleil, la partie de la Lune la plus proche de la Terre est sombre, nous ne pouvons donc pas voir la Lune, cette phase s’appelle la Nouvelle Lune.
-
Lorsque la Terre est entre le Soleil et la Lune, la partie de la Lune la plus proche de la Terre est la moitié éclairée, cette phase est appelée Pleine Lune.
-
Lorsque la Lune est dans des positions intermédiaires, seule la moitié de la partie la plus proche de la Terre est éclairée. Par conséquent, nous ne voyons qu’un quart de Lune, ces deux phases sont appelées Quarts, Croissantes ou décroissantes selon que la partie éclairée visible depuis la Terre a tendance à croître ou à diminuer.
Note: Ce programme interactif tente d’expliquer les phases de la Lune, mais il s’agit d’une représentation fidèle de l’orbite de la Lune, qui forme un angle de 5 ° avec le plan de l’écliptique (l’orbite terrestre autour du Soleil), ou l’orientation de l’axe de la Terre qui est d’environ 23º avec la normale au plan de l’écliptique.
Une ligne rouge a été tracée sur la Lune afin que le lecteur puisse apprécier la coïncidence de la période de rotation de la Lune autour de son axe et du temps nécessaire pour compléter une orbite autour de la Terre et donc la Lune a toujours la même face à la Terre.
Éclipses de Lune
Les éclipses de Lune se produisent chaque fois que la Lune est en Pleine phase et chaque fois que le Soleil, la Terre et la Lune sont en ligne droite. Ensuite, la Lune est dans l’ombre produite par la Terre comme le montre la figure.
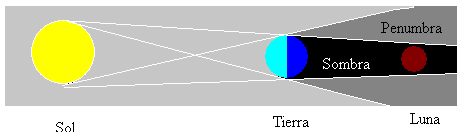
Il existe d’autres types d’éclipse lunaire, qui dépendent de l’alignement des trois corps célestes. La Lune peut être dans une zone non éclairée (ombre) ou partiellement éclairée (pénombre).
L’Éclipse solaire se produit lorsque la Lune se tient entre le Soleil et la Terre, la Lune est dans une Nouvelle phase. La Lune est 400 fois plus petite que le Soleil mais la Lune est 400 fois plus proche de la Terre, donc la taille apparente des deux corps vus de la Terre est presque la même. La Lune peut ainsi produire une éclipse totale du Soleil, si elle est observée dans la zone d’ombre projetée par la Lune sur Terre.
Données sur la Lune
| Masse (kg) | 7.349·1022 |
| Rayon (km) | 1737. 4 |
| Densité moyenne (g/cm3) | 3.34 |
| distance moyenne à la Terre (km) | 384 000 |
| Période d’orbite (jours) | 27.32166 |
| Accélération de la gravité à l’équateur (m/s2) | 1.62 |
| Excentricité de l’orbite | 0.0549 |
| Inclinaison de l’orbite (degrés) | 5.1454 |
-
Calculez le rayon de l’orbite circulaire de la Lune autour de la Terre en sachant que la période est de 27,32 jours. Calculez également la vitesse de la Lune. Données: G = 6,67 * 10-11 Nm2 / kg2, la masse de la Terre est de M = 5,98 * 1024 kg.
-
Calculez l’accélération de la gravité g à la surface de la Lune.
-
Calculez le quotient entre le diamètre du Soleil et le diamètre de la Lune. Calculez le rapport entre la distance moyenne entre le Soleil et la Terre, et la Lune et la Terre. Données: Rayon du soleil 6,96 * 108 m, distance Terre du milieu-Soleil 1,49 * 1011 m
-
Calculez la position du centre de masse du système Terre-Lune, mesurée à partir du centre de la Terre.
-
Calculez la force d’attraction de la Terre sur la Lune, comparez-la à la force d’attraction du Soleil sur la Lune. Référence: Masse solaire, 1,98 * 1030 kg
Références
M. Marov. Planètes du Système Solaire. Maison d’édition Mir.
En savoir plus sur les planètes Dans Combien de planètes y a-t-il dans notre système solaire?. ComofuncionaQue.com
Pour la section ‘Trajectoire de la Lune’
David C. Johnston. Chemins cycloïdaux en physique en tant que superpositions de mouvements de translation et de rotation. Être. J. Phys.87 (10), Octobre 2019, pp. 808-810
La Lune Vire Toujours Vers le Soleil. Pages de mathématiques.