Modèle de Markov caché: Définition et aperçu simples

Définitions statistiques >

Le modèle de Markov caché (HMM) est un moyen relativement simple de modéliser des données séquentielles. Un modèle de Markov caché implique que le modèle de Markov sous-jacent aux données vous est caché ou inconnu. Plus précisément, vous ne connaissez que des données d’observation et non des informations sur les États. En d’autres termes, il existe un type spécifique de modèle qui produit les données (un modèle de Markov) mais vous ne savez pas quels processus les produisent. Vous utilisez essentiellement vos connaissances des modèles de Markov pour faire une supposition éclairée sur la structure du modèle.

Qu’est-ce qu’un modèle Markov ?

Pour découvrir le Modèle de Markov Caché, vous devez d’abord comprendre ce qu’est un Modèle de Markov. Ici, je vais créer un exemple simple en utilisant deux éléments très familiers en probabilité: des dés et des sacs de boules colorées.

Les composants du modèle, que vous utiliserez pour créer le modèle aléatoire, sont:

• Un dé rouge à six faces.
• Une matrice noire à dix faces.
• Un sac rouge avec dix boules. Neuf boules sont rouges, une est noire.
• Un sac noir avec vingt balles. Une boule est rouge, dix-neuf sont noires.

 » Noir » et « Rouge » sont les deux états de ce modèle (en d’autres termes, vous pouvez être noir ou vous pouvez être rouge).
Créez maintenant le modèle en suivant ces étapes :

1. ÉTAPE D’ÉMISSION: Rouler un dé. Notez le nombre qui apparaît. C’est l’émission. Dans le graphique ci—dessus, j’ai choisi un dé rouge pour commencer (arbitraire – j’aurais pu choisir le noir) et j’ai roulé 2.
2. ÉTAPE DE TRANSITION: Choisissez au hasard une balle dans le sac avec la couleur qui correspond au dé que vous avez roulé à l’étape 1. J’ai roulé un dé rouge, alors je vais choisir une balle dans le sac rouge. J’ai sorti une boule noire, donc je vais passer au dé noir pour la prochaine émission.

Vous pouvez ensuite répéter ces étapes jusqu’à un certain nombre d’émissions. Par exemple, répéter cette séquence d’étapes 10 fois peut vous donner l’ensemble {2,3,6,1,1,4,5,3,4,1}. Le processus de transition d’un état à l’autre est appelé processus de Markov.

La transition du rouge au noir ou du noir au rouge comporte des probabilités différentes car il y a différents nombres de boules noires et rouges dans les sacs. Le diagramme suivant montre les probabilités pour ce modèle particulier, qui a deux états (noir et rouge):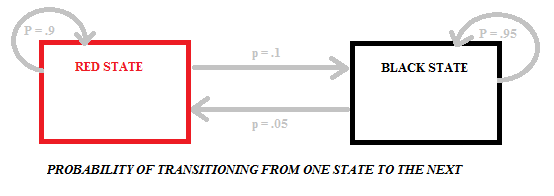

La notation cachée du modèle de Markov

λ =(A, B, π), est une notation abrégée pour un HMM. D’autres notations sont utilisées dans les modèles de Markov cachés:

• A = probabilités de transition d’état (aij)
• B = matrice de probabilité d’observation (bj(k))
• N = nombre d’états dans le modèle {1,2NN} ou l’état à l’instant t →st
• M = nombre de symboles d’observation distincts par état
• Q = {q0 , q1, . . . , qN-1} = états distincts du processus de Markov
• T = longueur de la séquence d’observation
• V = {0, 1,. . . , M-1 } = ensemble d’observations possibles
• O =(O0, O1,. . . , OT-1) = séquence d’observation
• π = distribution d’état initiale (ni)
• s = état ou séquence d’état (s1, s2… sn)
• xk = état caché
• zk = observation.

Trois problèmes de base

Trois problèmes de base peuvent être résolus avec des modèles de Markov cachés:

1. Étant donné le modèle de Markov Masquéλ = (A, B, π) et une séquence d’observations O, trouvez la probabilité d’une observation P (O |λ). C’est parfois ce qu’on appelle le problème de l’évaluation.
2. Étant donné le modèle de Markov Masquéλ= (A, B, π) et une séquence d’observation O, trouvez la séquence d’état la plus probable (s1, s2… sn). C’est parfois appelé un problème de décodage.
3. Trouvez une séquence d’observation (O1, O2OnOn et Modèle de Markov Caché λ = (A, B, π) qui maximise la probabilité de O. On parle parfois de Problème d’apprentissage ou d’optimisation.

Rabiner, L.R. « Un tutoriel sur les modèles de Markov cachés et les applications sélectionnées en reconnaissance vocale », Proceedings of the IEEE, vol.77, p. 257-286, Fév. 1989.
Timbre, M. (2013). Une Introduction Révélatrice aux Modèles cachés de Markov. Récupéré le 8/6/2013 de: http://www.cs.sjsu.edu/~stamp/RUA/HMM.pdf

——————————————————————————

Besoin d’aide pour une question de devoirs ou de test? Avec Chegg Study, vous pouvez obtenir des solutions étape par étape à vos questions d’un expert dans le domaine. Vos 30 premières minutes avec un tuteur Chegg sont gratuites!