Que sont les discussions numériques?

Les discussions numériques (ou « discussions mathématiques ») sont de courtes discussions entre un enseignant et des élèves sur la façon de résoudre un problème de mathématiques mentales particulier. L’accent n’est pas mis sur la bonne réponse, mais sur toutes les méthodes possibles pour trouver la réponse. Chaque élève a une chance d’expliquer sa méthode, et tout le monde apprendra des méthodes des autres!

Pour commencer une conversation numérique, l’enseignant donne aux élèves un COURT problème de mathématiques à résoudre — mais les élèves ne sont pas autorisés à utiliser une calculatrice ou un crayon papier &. L’idée est de le résoudre dans sa tête ! Par exemple, vous pouvez demander aux élèves de 4e à 12e année de résoudre 5 × 18 en utilisant les mathématiques mentales.

(La discussion ci-dessous est basée sur la vidéo de Jo Boaler sur les discussions numériques de son site web Youcubed.)

L’image ci-dessous montre des illustrations visuelles de QUATRE façons différentes de trouver 5 × 18. Ils se trouvent également dans la vidéo ci-dessous.

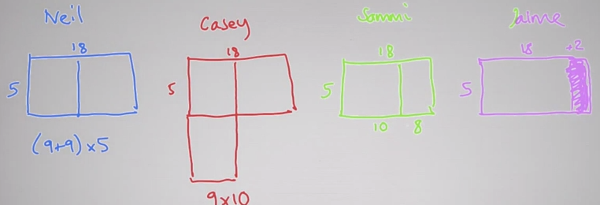
1. La méthode de Neil était de casser 18 en 9 + 9. Il a calculé 5 × 9 et 5 × 9, et les a ajoutés.
2. Casey a utilisé le doublement de moitié &: il a pris la moitié de 18 et le double de 5, et les a multipliés: 9 × 10 = 90.
3. Sammi a utilisé la propriété distributive, divisant 18 en 10 +8. Elle a multiplié 5 × 10 et 5 × 8 et les a ajoutés.
4. Jaime a résolu 5 × 20 = 100, puis en a soustrait 5 × 2.

Comme vous pouvez le constater, il existe en effet de nombreuses façons de résoudre ce problème!

Les discussions sur les nombres favorisent le sens des nombres — la capacité de travailler avec les nombres en les brisant et en les décomposant en parties. Et cette capacité s’est avérée être d’une importance primordiale pour que les étudiants puissent maîtriser l’algèbre.

D’autres problèmes que vous pouvez essayer sont 12 × 15 et 21 × 9. Bien sûr, vous pouvez utiliser ce concept avec d’autres opérations et avec des fractions et des décimales. Comment résoudrais-tu 2,75 × 20 ou 398 -199? Vous pouvez utiliser des additions et des soustractions à deux chiffres (telles que 25 + 26 et 71 − 32) pour les étudiants plus jeunes.

Voici une autre ressource pour les discussions numériques (ils les appellent « chaînes de nombres »): Numberstrings.com .

Jo Boaler de l’Université de Stanford a fait une très bonne vidéo sur les bases des discussions numériques. Veuillez le regarder ci-dessous pour en savoir beaucoup plus!

J’aime beaucoup le concept de discussions numériques. Les élèves peuvent voir qu’il existe de NOMBREUSES façons de voir le problème et de trouver la réponse. Il aide également les élèves à communiquer sur les mathématiques — qui sont une compétence très importante — et à devenir plus confiants en classe. En fait, les discussions numériques sont un excellent moyen d’aider les élèves à surmonter la peur de présenter leurs solutions aux autres, car les tâches sont courtes et relativement faciles (l’enseignant doit bien sûr ajuster le problème de mathématiques mentales au niveau des élèves).

Alors regardez la vidéo ci-dessus.

J’ai toujours mis l’accent sur le sens des nombres et les mathématiques mentales dans mes livres de mathématiques Gigantesques — à tel point que de nombreux enfants qui utilisent d’autres programmes de mathématiques ont des difficultés avec les questions de mathématiques mentales dans les tests de classement.

Certains de mes livres avec des stratégies de mathématiques mentales incluent:

• Ajouter & Soustraire 2-B — addition et soustraction de nombres à deux chiffres, y compris avec les mathématiques mentales
• Ajouter & Soustraire 3 – addition et soustraction de nombres à trois chiffres, y compris avec les mathématiques mentales
• Multiplication 2 — multiplication à plusieurs chiffres, y compris les problèmes de mathématiques mentales tels que 6 × 20 et 7 × 31
• Décimales 1 – introduction aux décimales. Vous apprendrez à résoudre des problèmes tels que 0,05 + 0,2 et 6 × 0,8 en utilisant les mathématiques mentales

Par Maria Miller