Un cercle est divisé uniformément en six triangles égaux

Salut Marilynn,

Tout d’abord, je vais vous dire mes hypothèses sur à quoi ressemble votre image:

1. Chaque triangle a un sommet (coin) au centre du cercle
2. Chaque triangle a des coins sur la circonférence du cercle (donc, deux côtés de chaque triangle est un rayon)
3. Les triangles partagent des côtés (il n’y a pas de baille entre les triangles)

L’image globale ressemble à une fleur – chaque triangle est un pétale.

La zone inconnue est ce qui reste autour de l’extérieur du cercle, entre la circonférence et le côté extérieur de chaque triangle. Cette zone inconnue est divisée en six sections congruentes (égales dans tous les sens – comme les triangles sont « égaux » dans tous les sens – y compris l’aire, la longueur du côté et la longueur de l’arc). Il n’est pas clair si vous voulez dire que l’aire d’un arc est Pi (pas réellement une tarte divisée, bien que prononcée de la même manière), ou que les six sections prises ensemble sont Pi. Dans ce qui suit, je supposerai que l’une des sections extérieures a une superficie de Pi, de sorte que la superficie des six sections prises ensemble est de 6 fois Pi. Nous devons trouver le rayon du cercle, appelez-le r.

J’utiliserai également P pour représenter Pi (ou env. 3.14). Maintenant, il y a beaucoup d’informations que nous pouvons garnir des triangles:

1. Les angles au centre sont tous de 60 degrés. En effet, les six angles au centre sont tous égaux et un cercle a 360 degrés. Il en va de même pour 360, divisés par 6.
2. Chaque triangle est isocèle. En effet, deux côtés sont égaux (les côtés qui sont un rayon).
3. Chaque triangle est en fait équilatéral. Parce qu’il s’agit d’iscocèles, les deux angles extérieurs sont également égaux. Mais il y a 180 degrés dans un triangle, 60 sont déjà utilisés dans l’angle central, laissant 180-60 = 120 degrés pour les angles extérieurs. Mais, 120 divisé par 2 est de 60 degrés, donc les trois angles sont égaux, il s’agit donc d’isoscles.
4. Chaque côté de chaque triangle est de longueur r. C’est parce que nous avons 6 triangles équilatéraux congruents (« égaux » dans tous les sens), et parce que deux côtés de chaque triangle est un rayon.

À partir de la géométrie des triangles, nous devons faire de l’algèbre. Parce que nous connaissons une aire et que nous avons besoin d’un rayon, nous avons besoin d’une formule (ou d’une équation) pour le rayon en termes d’aire (dans ce qui suit, gardez à l’esprit l’objectif d’une formule). L’aire du cercle est P * r2 (r2 signifie r au carré, et * signifie multiplier) L’aire des sections restantes à l’extérieur des triangles, mais à l’intérieur du cercle (une aire que nous n’avons déjà pas 6 * P), peut également être trouvée en soustrayant l’aire des triangles de l’aire du cercle. Nous devons trouver une zone de l’un des triangles équilatéraux.

Méthode 1 pour calculer une aire d’un triangle
L’aire d’un triangle est b * h / 2 C’est là qu’une trigonométrie est nécessaire: Tracez une ligne d’un sommet à un côté opposé qui divise le côté opposé en deux et est à angle droit. Cela divise le triangle équilatéral en deux triangles rectangles congruents, et le nouveau côté est la hauteur, appelez-le h. Nous devons trouver h.

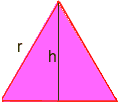
En utilisant trig dans l’un des triangles rectangles, nous avons sin60 = h / r Mais sin60 = sqr(3) / 2, où sqr(3) signifie la racine carrée de trois, donc sqr(3) / 2 = h / r multiplie les deux côtés par r pour obtenir h = r * sqr(3) / 2 r Maintenant, l’aire d’un triangle équilatéral est b * h / 2 =(r) *(r * sqr(3)/2)/2 = ( r2) * sqr(3) / 4 r = sqr(6 *P /(P-6 * sqr(3) / 4)) Utilisez l’ordre des opérations pour calculer sur une calculatrice (avec P = 3,14): r = 5,896… Ainsi, le rayon du cercle est d’env. 5.9. Paul