Utiliser des logarithmes dans le Monde Réel

Les logarithmes sont partout. Avez-vous déjà utilisé les phrases suivantes?

• 6 chiffres
• Deux chiffres
• Ordre de grandeur
• Taux d’intérêt

Vous décrivez les nombres en fonction de leurs puissances de 10, un logarithme. Et un taux d’intérêt est le logarithme de la croissance d’un investissement.

Surpris que les logarithmes soient si courants? Moi aussi. La plupart des tentatives de mathématiques Dans le Monde réel (TM) soulignent les logarithmes dans une formule arcanique, ou prétendent que nous sommes des géologues fascinés par l’échelle de Richter. « Les scientifiques se soucient des journaux, et vous devriez aussi. Aussi, pouvez-vous imaginer un monde sans zinc? »

Non, non, non, non non, non non! (Maman mia!)

Les mathématiques expriment des concepts avec des notations comme « ln » ou « log ». Trouver « les mathématiques dans le monde réel » signifie rencontrer des idées dans la vie et voir comment elles pourraient être écrites avec la notation. Ne cherchez pas les symboles littéraux! À quand remonte la dernière fois que vous avez écrit un signe de division ? À quand remonte la dernière fois que vous avez coupé de la nourriture?

Ok, ok, on comprend: de quoi parlent les logarithmes ?

Les logarithmes trouvent la cause d’un effet, c’est-à-dire l’entrée pour une sortie

Un « effet » courant consiste à voir quelque chose grandir, comme passer de \$100 à \ \150 en 5 ans. Comment cela s’est-il passé? Nous ne sommes pas sûrs, mais le logarithme trouve une cause possible: un retour continu de ln (150/100) / 5 = 8,1% expliquerait ce changement. Ce n’est peut-être pas la cause réelle (toute la croissance s’est-elle produite au cours de la dernière année?), mais c’est une moyenne lisse que nous pouvons comparer à d’autres changements.

D’ailleurs, la notion de « cause à effet » est nuancée. Pourquoi 1000 est-il plus grand que 100?

• 100 est 10 qui a grandi d’elle-même pendant 2 périodes ($10 * 10$)
• 1000 est 10 qui a grandi de lui-même pendant 3 périodes de temps ($10 * 10 * 10$)

Nous pouvons considérer les nombres comme des sorties (1000 est « 1000 sorties ») et des entrées (« Combien de fois 10 doit-il croître pour faire ces sorties? »). Donc,

1000 outputs > 100 outputs

parce que

3 inputs > 2 inputs

Ou en d’autres termes:

log(1000) > log(100)

Pourquoi est-ce utile?

Les logarithmes placent les nombres à une échelle humaine.

De grands nombres nous brisent le cerveau. Des millions et des billions sont « vraiment gros » même si un million de secondes représente 12 jours et un billion de secondes représente 30 000 ans. C’est la différence entre une année de vacances américaine et l’ensemble de la civilisation humaine.

L’astuce pour surmonter la « cécité des nombres énormes » consiste à écrire des nombres en termes d' »entrées » (c’est-à-dire leur base de puissance 10). Cette échelle plus petite (0 à 100) est beaucoup plus facile à saisir:

• puissance de 0 = $10^0$ = 1 (un seul article)
• puissance de 1 = $10^1$ = 10
• puissance de 3 = $10^3$ = mille
• puissance 6 = $10^6$ = millions de dollars
• puissance de 9 = $10^9$ = milliards de dollars
• puissance de 12 = $10^12$ = billion
• puissance de 23 = $10^23$ = nombre de molécules dans une dizaine de grammes de carbone
• puissance de 80 = $10^80$ = nombre de molécules dans l’univers

Une échelle de 0 à 80 nous a pris à partir d’un seul point pour le nombre de choses dans l’univers. Pas trop minable.

Les logarithmes comptent la multiplication en étapes

Les logarithmes décrivent les changements en termes de multiplication: dans les exemples ci-dessus, chaque étape est 10 fois plus grande. Avec le log naturel, chaque pas est « e » (2.71828…) fois plus.

Lorsqu’il s’agit d’une série de multiplications, les logarithmes aident à les « compter », tout comme les additions pour nous lorsque des effets sont ajoutés.

Montrez-moi le calcul

Temps pour la viande: voyons où les logarithmes apparaissent!

Salaire à six chiffres ou dépense à 2 chiffres

Nous décrivons les nombres en termes de leurs chiffres, c’est-à-dire combien de pouvoirs de 10 ils ont (sont-ils dans les dizaines, les centaines, les milliers, les dix-milliers, etc.). Ajouter un chiffre signifie « multiplier par 10 », c’est-à-dire

Les logarithmes comptent le nombre de multiplications ajoutées, donc en commençant par 1 (un seul chiffre), nous ajoutons 5 chiffres supplémentaires (110^ 55) et 100 000 obtiennent un résultat à 6 chiffres. Parler de « 6 » au lieu de « cent mille » est l’essence des logarithmes. Cela donne un sens approximatif de l’échelle sans sauter dans les détails.

Question bonus: Comment décririez-vous 500 000? Dire « chiffre 6 » est trompeur car les chiffres 6 impliquent souvent quelque chose de plus proche de 100 000. Le « chiffre 6.5 » fonctionnerait-il?

Pas vraiment. Dans nos têtes, 6,5 signifie « à mi-chemin » entre 6 et 7 chiffres, mais c’est un état d’esprit d’additionneur. Avec logarithmes a ».5″ signifie à mi-chemin en termes de multiplication, c’est-à-dire la racine carrée ($9^.5 means signifie que la racine carrée de 9 — 3 est à mi-chemin en termes de multiplication car elle est de 1 à 3 et de 3 à 9).

En prenant log (500 000), nous obtenons 5,7, ajoutons 1 pour le chiffre supplémentaire, et nous pouvons dire « 500 000 est un 6.7 chiffre numéro « . Essayez-le ici:

Ordre de grandeur

Nous, les geeks, adorons cette phrase. Cela signifie à peu près « différence 10x », mais cela semble plus cool que « 1 chiffre plus grand ».

Dans les ordinateurs, où tout est compté avec des bits (1 ou 0), chaque bit a un effet de doublement (pas 10x). Donc, passer de 8 à 16 bits est « 8 ordres de grandeur » ou $2 ^8 = 256 times fois plus grand. (« Plus grand » dans ce cas se réfère à la quantité de mémoire qui peut être adressée.) Passer de 16 à 32 bits signifie 16 ordres de grandeur supplémentaires, ou $2^16 ~ ~ 65 536 fois plus de mémoire pouvant être adressée.

Taux d’intérêt

Comment calculons-nous les taux de croissance? Un pays n’a pas l’intention de croître à 8,56% par an. Vous regardez le PIB une année et le PIB l’année suivante, et prenez le logarithme pour trouver le taux de croissance implicite.

Mes deux interprétations préférées du logarithme naturel (ln(x)), c’est-à-dire le logarithme naturel de 1.5:

• En supposant une croissance de 100%, combien de temps devez-vous croître pour atteindre 1,5? (.405, moins de la moitié de la période)
• En supposant 1 unité de temps, à quelle vitesse devez-vous croître pour atteindre 1,5? (40.5 % par an, composés en continu)

Les logarithmes sont la façon dont nous déterminons à quelle vitesse nous grandissons.

Échelle de mesure: Google PageRank

Google donne à chaque page du Web un score (PageRank) qui est une mesure approximative de l’autorité / de l’importance. C’est une échelle logarithmique, qui dans ma tête signifie « PageRank compte le nombre de chiffres dans votre score ».

Ainsi, un site avec pagerank 2 (« 2 chiffres ») est 10 fois plus populaire qu’un site PageRank 1. Mon site est PageRank 5 et CNN a PageRank 9, donc il y a une différence de 4 ordres de grandeur ($10^4$ = 10,000).

Grosso modo, je reçois environ 7000 visites/jour. En utilisant mes calculs d’enveloppe, je peux deviner que CNN reçoit environ 7000 * 10 000 = 70 millions de visites / jour. (Comment ai-je fait ça? Dans ma tête, je pense que7 7k * 10k = 70 * k * k = 70 * M$). Ils pourraient en avoir quelques fois plus que cela (100M, 200M) mais probablement pas jusqu’à 700M.

Google transmet beaucoup d’informations avec une échelle très approximative (1-10).

Échelle de mesure: Richter, Décibel, etc.

Soupir. Nous en sommes à l’exemple typique des « logarithmes dans le monde réel »: échelle de Richter et décibels. L’idée est de mettre les événements qui peuvent varier considérablement (tremblements de terre) sur une seule échelle avec une petite plage (généralement de 1 à 10). Tout comme le PageRank, chaque augmentation de 1 point est une amélioration de puissance de 10 fois. Le plus grand tremblement de terre enregistré par l’homme était de 9,5; l’impact de la péninsule du Yucatán, qui a probablement fait disparaître les dinosaures, était de 13.

Les décibels sont similaires, bien qu’ils puissent être négatifs. Les sons peuvent passer d’intensément silencieux (goutte d’épingle) à extrêmement bruyant (avion) et notre cerveau peut tout traiter. En réalité, le son du moteur d’un avion est des millions (des milliards, des billions) de fois plus puissant qu’un pindrop, et il est gênant d’avoir une échelle qui va de 1 à un gazillion. Les journaux gardent tout à une échelle raisonnable.

Graphes logarithmiques

Vous verrez souvent des éléments tracés sur une « échelle de journal ». Dans ma tête, cela signifie qu’un côté compte le « nombre de chiffres » ou le « nombre de multiplications », pas la valeur elle-même. Encore une fois, cela permet de montrer des événements très variés sur une seule échelle (allant de 1 à 10, pas de 1 à des milliards).

La loi de Moore en est un excellent exemple: nous doublons le nombre de transistors tous les 18 mois (image reproduite avec l’aimable autorisation de Wikipedia).

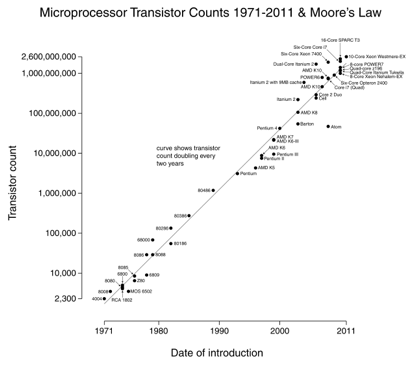
La chose intéressante à propos des graphes à échelle log est que les changements exponentiels (vitesse du processeur) apparaissent comme une ligne droite. Une croissance de 10 fois par an signifie que vous progressez régulièrement dans l’échelle des « chiffres ».

En avant et en haut

Si un concept est bien connu mais pas bien aimé, cela signifie que nous devons construire notre intuition. Trouvez les analogies qui fonctionnent, et ne vous contentez pas de la pente qu’un manuel va trotter. Dans ma tête:

• Les logarithmes trouvent la cause première d’un effet (voir croissance, trouver le taux d’intérêt)
• Ils aident à compter les multiplications ou les chiffres, avec en prime des comptages partiels (500k est un nombre à 6,7 chiffres)

Bon calcul.

Autres Articles De Cette Série

1. Un Guide Intuitif Des Fonctions Exponentielles & e
2. Démystifier le Logarithme Naturel (ln)
3. Un Guide Visuel des Taux d’Intérêt Simples, Composés et Continus
4. Définitions Communes de e (Colorisé)
5. Comprendre les exposants (Pourquoi 0^0 = 1?)
6. Utiliser des Logarithmes dans le Monde Réel
7. Comment Penser Avec Des Exposants Et Des Logarithmes
8. Comprendre La Croissance Discrète par rapport À La Croissance Continue
9. Que signifie vraiment un exposant?
10. Q: Pourquoi e est-il spécial? (2.718…, pas 2, 3,7 ou un autre numéro?)