A Naprendszer: a Föld és a Hold
a bolygók tíz-és százmillió kilométerre vannak tőlünk. Az ilyen nagy számok használatának elkerülése érdekében a csillagászati egységet (Au) a távolság mértékegységeként, azaz a Föld és a nap közötti átlagos távolság 149.600.000 km.A fény 8 perc 19 másodpercet vesz igénybe, hogy megtegye ezt a távolságot.
a Naprendszer mérete meghaladja a Plútó pályáját 40 AU-nál, és úgy definiálják, hogy a nap vonzóereje megegyezik a hozzánk legközelebb eső csillagok vonzóerejével. A Naprendszer méretei ekkor 1, 5 105 AU nagyságúak lennének. Nyilvánvaló, hogy ezek a méretek nagyon kicsiek a galaxis vagy a látható univerzum méreteihez képest. Az ilyen hatalmas távolságok mérésére szolgáló egységek a fényév és a parsec, amely 206 265 AU vagy 3,26 fényévnek felel meg.
a Naprendszer bolygói két csoportra oszthatók: a Merkúr, a Vénusz, a Föld és a Mars által alkotott földi csoportra, valamint az óriásbolygók csoportjára, amelyet a Jupiter, a Szaturnusz, az Uránusz és a Neptunusz alkot.
a Vénusz és a Merkúr kivételével minden bolygó rendelkezik műholdakkal, amelyek többsége az óriásbolygókhoz tartozik. A Föld, a Jupiter, a Szaturnusz és a Neptunusz rendelkezik a legnagyobb műholdakkal: a Hold, a Jupiter műholdjai, amelyeket Galileo fedezett fel (Io, Europa, Ganymede, Callisto), a Szaturnusz műholdas titánja és a Neptunusz Tritonja.
az aszteroidák hatalmas gyűrűs régiót foglalnak el a Mars és a Jupiter pályái között, átlagosan 2,75 AU távolságra a naptól. A legnagyobb aszteroida a Ceres, amelynek átmérője 1000 km.
az üstökösök, amelyeket 600 körül katalogizáltak, két csoportra oszthatók: rövid (20 év alatt) és hosszú (20 év felett). Számos hipotézis létezik az üstökösök eredetéről, köztük a holland csillagász J. Oort.
a bolygóközi térben említett testeken kívül számos különböző méretű részecske van, főleg azok, amelyek tömege ezred vagy milliomod gramm, amelyeket meteorikus pornak neveznek. Ezeknek a részecskéknek a kialakulása valószínűleg a nagyobb testek (aszteroidák) ütközésének és a Naprendszer létezésének és evolúciójának egymást követő széttöredezettségének köszönhető.
a meteorikus por felelős a zodiákus fény jelenségéért, amelyet alkonyat után vagy hajnal előtt figyelnek meg, mivel ezek a porrészecskék szétszórják a fényt. A legtöbb részecske elpárolog, amikor belép a Föld légkörébe (80-120 km magasságban), csak kis része éri el a Föld felszínét.
most nézzük meg a Naprendszer bolygóival kapcsolatos adatokat
először a nap
| égitest | Rádió | tömeg |
|---|---|---|
| V | 6,96·108 m | 1,98 * 1030 kg |
azután, ki a földről
| égitest | fél-fő tengely | időszak | tömeg |
|---|---|---|---|
| Föld | 149,6·109 m | 1 év=365,26 nap | 5.98·1024 kg |
a többi bolygó
| bolygó | fél-nagy tengely (AU) | excentricitás | időszak (év) | tömeg |
|---|---|---|---|---|
| higany | 0.387 | 0.206 | 0.24 | 0.06 |
| Vénusz | 0.723 | 0.007 | 0.62 | 0.82 |
| Föld | 1.000 | 0.017 | 1.00 | 1.00 |
| Mars | 1.524 | 0.093 | 1.88 | 0.11 |
| Jupiter | 5.203 | 0.048 | 11.86 | 318 |
| Szaturnusz | 9.539 | 0.056 | 29.46 | 95.1 |
| Uránusz | 19.182 | 0.047 | 84.01 | 14.6 |
| Neptunusz | 30.058 | 0.009 | 164.8 | 17.2 |
az alábbi táblázat kiegészítő adatokként szolgál:
- a bolygó pályájának síkjának dőlése az ekliptikához képest (a Föld pályájának síkja)
- a tengelye körüli forgási idő. Nagyon nehéz volt mérni ezt a nagyságrendet olyan bolygóknál, mint a Merkúr és a Vénusz. A Jupiter, a Szaturnusz, az Uránusz és a Neptunusz gázhéjai rendelkeznek a differenciális forgás tulajdonságával, Vagyis forgási periódusuk a szélességtől függően változik.
- a forgástengely dőlése a pálya síkjához viszonyítva. A Vénusz esetében ez 177 6x, ami egyenértékű azzal, hogy azt mondjuk, hogy a tengely dőlésszöge 3, de a forgásirány inverz. Ugyanez az érv vonatkozik az Uránuszra is, ami azt jelzi, hogy az urán forgástengelye szinte pályája síkjában van.
| bolygó | a pálya dőlésszöge | forgási periódus | sűrűség g/cm3 | rádió Egyenlítő (km) | tengely dőlés | nem. műholdak |
|---|---|---|---|---|---|---|
| higany | 7.0 | 58d.6 | 5.44 | 2 439 | <30 ons | 0 |
| Vénusz | 3.4 | 243d | 5.24 | 6 051 | 177 ° | 0 |
| Föld | 0 | 23 óra.9 | 5.52 | 6 378 | 23.5 | 1 |
| Mars | 1. 8 | 24 óra.6 | 3.95 | 3 394 | 25 db.2 | 2 |
| Jupiter | 1st. 3 | 9h.9 | 1.33 | 71 398 | 3.1 | 16 |
| Szaturnusz | 2.5 | 10 óra.2 | 0.69 | 60 000 | 26 db.4 | 17 |
| Uránusz | 0 ons.8 | 10 óra.8 | 1.26 | 25 400 | 98 ons | 5 |
| Neptunusz | 1. 8 | 15 óra.8 | 1.67 | 24 750 | 29 ons | 2 |
műholdak
végül néhány adatot szolgáltatunk a bolygók főbb műholdjairól. A Jupiternek és a Szaturnusznak sok olyan műholdja van, amelyek sokkal nagyobbak, mint a Marsé, de csak azokat említjük, amelyek hasonló méretűek vagy nagyobbak, mint a Holdunk.
| bolygó | műholdak | sűrűség g/cm3 | átlagos sugár (km) | Rádiópálya (103 km) | időszak (napok) |
|---|---|---|---|---|---|
| Föld | Hold | 3.33 | 1 738 | 384.4 | 27.32 |
| Mars | Phobos | 2.1 | 13.5 | 9.38 | 0.319 |
| Deimos | 2.1 | 7.5 | 23.46 | 1.262 | |
| Jupiter | Io | 3.53 | 1 820 | 421.6 | 1.769 |
| Európa | 3.03 | 1 565 | 670.9 | 3.551 | |
| Ganümédész | 1.93 | 2 638 | 1 070 | 7.155 | |
| Calisto | 1.83 | 2 410 | 1 880 | 16.689 | |
| Szaturnusz | Titán | 1.9 | 2 575 | 1 221.9 | 15.95 |
| Neptunusz | Gőte | 2 200 | 394.7 | 5.84 |
tevékenységek
- határozza meg a Jupiter bolygó tömegét a rádióadatokból és az egyik műhold forradalmi időszakából.
- határozza meg a Jupiter bolygó műholdjának pályájának sugarát a bolygó tömegéből és a műhold forradalmi időszakából.
- határozza meg a G gravitációs mező intenzitását a bolygók és egyes műholdak felszínén m tömegük és R sugaruk, vagy sűrűségük és sugaruk adatai alapján.
példa: határozzuk meg a Jupiter bolygó tömegét, tudva, hogy az Io pályájának sugara 421 600 km, a fordulási ideje pedig 1769 nap. Tény: a G állandó értéke 6,67 * 10-11 Nm2 / kg2
példa: Számítsa ki a Callisto műhold pályájának sugarát, tudva, hogy forradalmi periódusa 16,689 nap, a Jupiter bolygó tömege pedig 1,901·1027 kg. Adatok: a G állandó értéke 6,67 * 10-11 nm2 / kg2
g=G M R 2 = 4 ons 3 GPR
adatok: a G állandó 6.67 * 10-11 Nm2 / kg2
a Hold
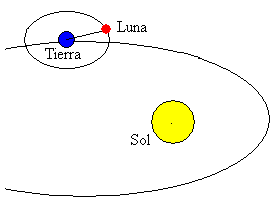
a Hold a Naprendszer egyik legnagyobb teste. Pályája majdnem kör alakú (excentricitás=0,05), pályája síkja pedig 5 db-ra hajlik a Föld pályájának síkjához képest.
a Föld és a Hold középpontja közötti átlagos távolság 384 400 km.Forgási ideje a Föld körül 27 322 nap. A Hold helyzetének változása a Naphoz képest a hold fázisait eredményezi.
a Hold mindig ugyanazt az arcot mutatja a földi megfigyelőnek, a Föld által a Holdra gyakorolt árapályerők hatása miatt. Ami azt jelenti, hogy a Hold tengelye körüli forgási ideje egybeesik azzal az idővel, amely a Föld körüli pálya befejezéséhez szükséges.
a Hold az égi tárgy, amely leginkább lenyűgözte az emberi fajt. A volt Szovjetunió először küldött egy automatikus hajót, amely 1959-ben landolt a Hold felszínén. Július 20, 1969 Neil Armstrong kíséretében Edwin Aldrin voltak az első emberek járni a felszínen a Hold részeként az Apollo 11 küldetés. Az amerikai űrhajósok utolsó látogatására a Holdra 1972-ben került sor.
a Hold eredete bizonytalannak tűnik, számos elmélet létezik:
-
egyidejűleg alakult ki a Föld a köd anyagával
-
az égitest két részre oszlik, így létrejön a Föld és a Hold
-
hogy a Hold máshol alakult ki, és a Föld elfogta
-
hogy a Föld összeütközött egy nagy méretű (körülbelül Mars méretű vagy annál nagyobb) égi objektummal, és hogy a Hold az ütközésből kiűzött anyaggal jött létre.
ez utóbbi elmélet jelenleg a tudományos közösség által leginkább elfogadottnak tűnik.
Hold Út
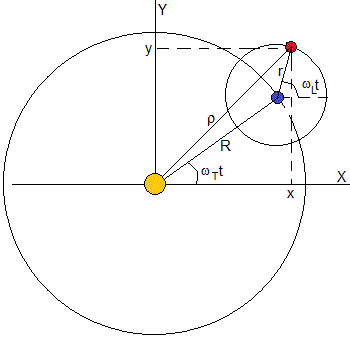
Fontolja meg egy bolygót, valamint a műhold. A bolygó írja le egy kör alakú pályán az R sugarú körbe a csillag állandó szögsebesség wT=2π/PT, PT, hogy az az időszak, vagy az idő, hogy vezet egy teljes fordulatot. A műholdas írja le egy kör alakú pályán coplanaria az r sugarú állandó szögsebesség wL=2π/PL, hogy PL az az időszak, vagy idő kell ahhoz, hogy egy teljes forradalom
a helyzet a műholdas tekintetében a referencia rendszer, amelynek eredete a csillag, az
x=Rcos( ω T )+rcos( ω L-t), y=Risiko( ω T )+risiko( ω L-t )
α=wT/wL
{ x=Rcos( α-ω L t )+rcos( ω L-t), y=Risiko( α-ω L t )+risiko( ω L-t ) { x=Rcos( 2π α O L t )+rcos( 2π O L t ) y=Risiko( 2π α O L t )+risiko( 2π O L t )
Hívjuk τ=t/PL
x R =cos( α·2πτ )+ r r cos( 2πτ ), illetve R =sin( α·2πτ )+ r r sin( 2πτ )
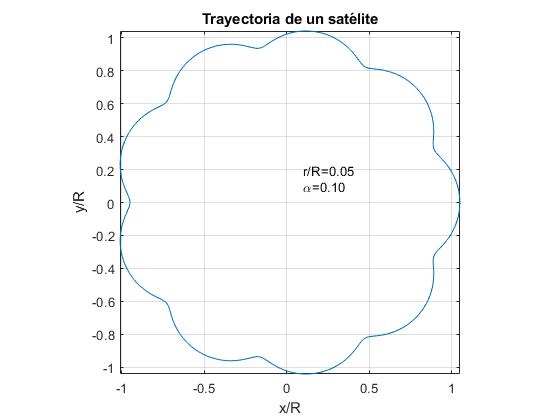
mi Képviseljük a pályára egy műholdat α=0.1, illetve a három érték aránya r/R
- r/R<α. Például, r / R=0.05
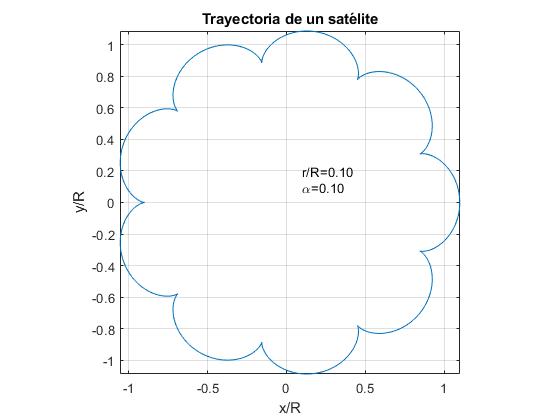
- r/R=α. Például, r / R=0.1
- r/R >α. Például, r / R=0.15
alfa=0.1;r=0.15;fplot(@(t) r*cos(2*pi*t)+cos(2*pi*alfa*t), @(t) r*sin(2*pi*t)+sin(2*pi*alfa*t),)text(0.1,0.1,sprintf('\alpha=%1.2f',alfa))text(0.1,0.2,sprintf('r/R=%1.2f',r))axis equalgrid onxlabel('x/R')ylabel('y/R')title('Trayectoria de un satélite')
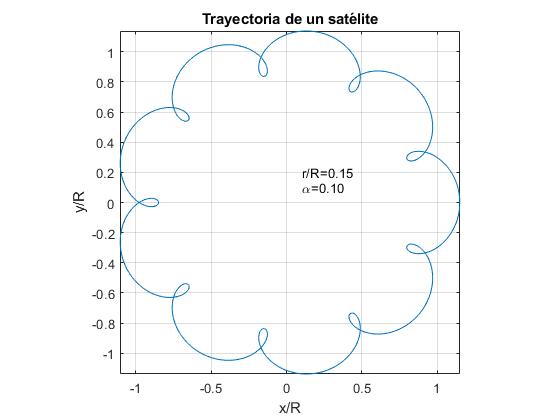
az eset a Föld, a Hold, az adatok:
- sugara, a Hold körüli pályára: r=384.4·106 m, időtartam PL = 27.32 d
- sugár a Föld körüli pályán: R = 149,6 * 109 m, PT időszak = 365,26 d
ons=tömeg/szélesség=PL/PT=0,0748. r / R=0,0026
a Hold pályája hasonlít az első számra. A grafikus ábrázolása a pályára a Holdat, hogy ezek az értékek az α r/R nem értékelem a rezgések a radiális távolság a Nap, a Hold
Gyorsulás a Hold
A távolság ρ a Nap, a Hold, a
ρ 2 = x 2 + y 2 = R 2 + r 2 +2rRcos( ( ω L − ω T), t )
kiszámítjuk a téglalap alakú alkatrészek gyorsulás
{ dx dt =− ω T Risiko( ω T )− ω L risiko( ω L-t ) dy dt = ω T Rcos( ω T )+ ω L rcos( ω L-t ) { x = d 2 x d t 2 =− ω T 2 Rcos( ω T )− ω L 2 rcos( ω L-t), y = d 2 y d t 2 =− ω T 2 Risiko( ω T )− ω L 2 risiko( ω L-t )
a radiális komponense A gyorsulás
hogy ρ = a → · ρ → ρ = x x+ y-x 2 + y 2 =− ω T 2 R 2 + ω L 2 r 2 +( ω T 2 + ω L 2 )Rrcos( ( ω L − ω T), t ) R 2 + r 2 +2 rr cos( ( ω L − ω T), t )
A minimális, illetve a maximális értéket kapunk, ha cos((wL-wT)t)=±1
egy max =− ω T 2 R 2 + ω L 2 r 2 +( ω T 2 + ω L 2 )Rr R 2 + r 2 +2 rr =−( ω T 2 R+ ω L 2 r ) min =− ω T 2 R 2 + ω L 2 r 2 −( ω T 2 + ω L 2 )Rr R 2 + r 2 -2 rr =−( ω T 2 R− ω L 2 r )
>> R=149.6e9; %Tierra>> r=384.4e3; %Luna>> wT=2*pi/(365*24*60*60) %velocidad angular TierrawT = 1.9924e-07>> wL=2*pi/(27.32*24*60*60) %velocidad angular TierrawL = 2.6619e-06>> aM=-(wT^2*R+wL^2*r)aM = -0.0059>> am=-(wT^2*R-wL^2*r)am = -0.0059
a Hold az egyetlen műhold a Naprendszerben, amelynek sugárirányú összetevője a gyorsulás negatív, azt mondják ,hogy’a Hold a Nap felé esik,’
a Hold fázisai
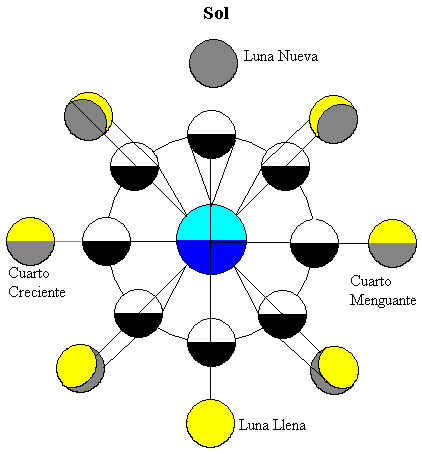
az ábra a Holdat különböző pozíciókban mutatja a Föld körüli pályáján. A nap messze van megvilágítva mindkét égitestet (az ábra tetején)
a Hold felét a nap világítja meg (fehér színben), a Földhöz legközelebb eső Hold felét pedig a földi megfigyelő látja. Mint a Hold mozog a Föld körül, látjuk a különböző frakciók a részét megvilágította a Nap (a sárga terület).
-
Amikor a Hold között, a Föld, a Nap, az a része, a Hold legközelebb a Föld sötét, így nem tudjuk a Hold, ez a szakasz az úgynevezett Új Hold.
-
Amikor a Föld között, a Nap, a Hold, az a része, a Hold legközelebb van a földhöz, a megvilágított felét, ebben a fázisban az úgynevezett Telihold.
-
Amikor a Hold a köztes pozíciók, csak a fele a legközelebbi része a Földön világít. Ezért mi csak a negyede, a Hold, a két fázis nevű Negyed, nő vagy Csökken, attól függően, hogy a megvilágított része látható a Földről a tendencia, hogy növekszik vagy csökken.
Megjegyzés: Ez az interaktív program megpróbálja megmagyarázni a hold fázisait, de ez a Hold pályájának hű ábrázolása, amely 5 db-os szöget képez az ekliptika síkjával (a Föld pályája a Nap körül), vagy a Föld tengelyének orientációja, amely körülbelül 23 db, a normál az ekliptika síkjához képest.
piros vonalat húztak a Holdon, hogy az olvasó értékelhesse a Hold tengelye körüli forgási periódusának egybeesését, valamint azt az időt, amely a Föld körüli pálya teljesítéséhez szükséges, ezért a Holdnak mindig ugyanaz az arca van a földdel.
holdfogyatkozások
holdfogyatkozások akkor fordulnak elő, amikor a Hold teljes fázisban van, és amikor a nap, a Föld és a Hold egyenes vonalban van. Ezután a Hold a Föld által termelt árnyékban van, amint az az ábrán látható.
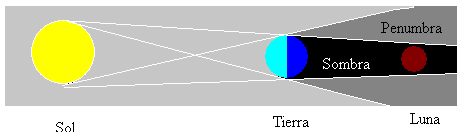
vannak más típusú holdfogyatkozások is, amelyek a három égitest összehangolásától függenek. A Hold lehet megvilágítatlan területen (árnyék) vagy részben megvilágított (félárnyék).
a Napfogyatkozás akkor következik be, amikor a Hold a nap és a Föld között áll, a Hold új fázisban van. A Hold 400-szor kisebb, mint a nap, de a Hold 400-szor közelebb van a Földhöz, tehát mindkét test látszólagos mérete a Földről nézve szinte azonos. A Hold tehát a nap teljes napfogyatkozását eredményezheti, ha megfigyelik a Hold által a Földön kivetített árnyékzónában.
Holdadatok
| Tömeg (kg) | 7.349·1022 |
| sugár (km) | 1737. 4 |
| átlagos sűrűség (g/cm3) | 3.34 |
| átlagos távolság a Földtől (km) | 384 000 |
| a pálya időtartama (napok) | 27.32166 |
| a gravitáció gyorsulása az egyenlítőn (m / s2) | 1.62 |
| a pálya excentricitása | 0.0549 |
| a pálya dőlése (fok) | 5.1454 |
-
Számítsa ki a Hold körpályájának sugarát a Föld körül, tudva, hogy az időszak 27,32 nap. Számítsa ki a Hold sebességét is. Adatok: G =6,67 * 10-11 Nm2 / kg2, a Föld tömege M=5,98 * 1024 kg.
-
Számítsa ki a G gravitáció gyorsulását a Hold felszínén.
-
Számítsa ki a nap és a Hold átmérője közötti hányadost. Számítsa ki a nap és a Föld, valamint a Hold és a Föld közötti átlagos távolság arányát. Adatok: nap sugara 6,96·108 m, Középfölde-nap távolság 1,49 * 1011 m
-
Számítsa ki a Föld-Hold rendszer tömegközéppontjának helyzetét, a Föld közepétől mérve.
-
Számítsa ki a Föld vonzerejét a Holdon, hasonlítsa össze a nap vonzerejével a Holdon. Nullapont: Nap tömege, 1,98 * 1030 kg
referenciák
M. Marov. A Naprendszer bolygói. Kiadó Mir.
További információ a bolygókról hány bolygó van a Naprendszerünkben?. ComofuncionaQue.com
a Hold pályájának szakaszához
David C. Johnston. Cikloidális utak a fizikában, mint a transzlációs és rotációs mozgások szuperpozíciói. Az vagyok. J. Phys.87 (10), 2019.október, 808-810
a Hold mindig a Nap felé fordul. Matek oldalak.