Bootstrap in R
a Bootstrap egy módszer a populációra vonatkozó következtetésekre a mintaadatok felhasználásával.Bradley Efron először mutatta be ebbenpapír 1979-ben.A Bootstrap a mintavételre támaszkodik a mintaadatok cseréjével. Ez a technika bármely statisztika standard hibájának becslésére használható, és ehhez konfidencia intervallumot (ci) kaphat. A Bootstrap különösen hasznosHa A CI-nek nincs zárt formája, vagy nagyon bonyolult.
tegyük fel, hogy van egy n elemből álló mintánk:X = {x1, x2,…, xn} és a T = t(X) statisztikai adatok CI-ben érdekeltek vagyunk. A Bootstrapframework egyszerű. Csak ismételjük meg a következő r-szorosátrendszer: az i-edik ismétléshez minta csere n elemekkel a rendelkezésre álló mintából (néhányat többször is kiválasztunk). Nevezzük ezt az új mintát i-edik bootstrap sample, Xiés calculatedesired statistic Ti = t (Xi).
ennek eredményeként statisztikánk R értékeit kapjuk: T1, T2,…, TR. Ennek alapján kiszámolhatjuk a CI-t a T-re. A percentilisek felvétele tűnik a legegyszerűbbnek.
Bootstrap működés közben
használjuk (még egyszer) a jól ismert iris adatkészletet. Vessen egy pillantást az első néhány sorra:
tegyük fel, hogy meg akarjuk találni a CIs-t a medián Sepal.Length, a mediánSepal.Width és a Spearman rangkorrelációs együtthatója között. A Rboot csomagját és egy függvényt fogjuk használni… boot. Ahhoz, hogy felhasználjuk erejét, létre kell hoznunk egy függvényt, amely kiszámítja a statisztikai adatokat az újramintázott adatokból. Legalább két érvet kell tartalmaznia: egy dataset és egy vektort, amely indices elemet tartalmaz egy adatkészletből, amelyet egy bootstrap minta létrehozásához választottak ki.
ha egyszerre több statisztika CIs-jét akarjuk kiszámítani, a függvényünknek egyetlen vektorként kell visszaadnia őket.
példánkban ez így nézhet ki:
library(boot)foo <- function(data, indices){ dt<-data c( cor(dt, dt, method='s'), median(dt), median(dt) )}foo kiválasztja a kívánt elemeket (mely számokat indices – ben tárolja)a data – ből, és kiszámítja az első két oszlop korrelációs együtthatóját (amethod='s' a Spearman rang együtthatójának kiválasztására szolgál, amethod='p' a Pearson-együtthatóval fog eredményezni) és azok mediánjait.
hozzáadhatunk néhány további érvet is, pl. hagyja, hogy a felhasználó válasszon típust odcorrelation coefficient:
foo <- function(data, indices, cor.type){ dt<-data c( cor(dt, dt, method=cor.type), median(dt), median(dt) )}ahhoz, hogy ez a bemutató általánosabb, fogom használni az utóbbi változatafoo.
most már használhatjuk a boot funkciót. Meg kell adnunk egy nevet oddataset, az imént létrehozott függvény, az ismétlések száma (R)és a függvényünk további argumentumai (például cor.type). Az alábbiakban iuse set.seed a példa reprodukálhatóságához.
set.seed(12345)myBootstrap <- boot(iris, foo, R=1000, cor.type='s')boot függvény egy objektumot az osztály hívott… (igen, igazad van!)boot. Két érdekes eleme van. $t a bootstrap eljárás által generált ourstatistic(s) R értékeit tartalmazza (bootstrap realizations ofT):
$t0 a statisztika (ok) értékeit tartalmazza eredeti, teljes, adatkészletben:
myBootstrap$t0## -0.1667777 5.8000000 3.0000000 boot objektum nyomtatása a konzolra további információkat nyújt:
original ugyanaz, mint $t0. A bias egy különbség a Bootstrap realizációk átlaga között (a $t – ból származók), az úgynevezett bootstrap estimateof T és az eredeti adatkészlet értéke (a $t0 – ból származók).
colMeans(myBootstrap$t)-myBootstrap$t0## 0.002546391 -0.013350000 0.007900000std. error a bootstrap becslés standard hibája, amely egyenlőa bootstrap megvalósítások standard eltérése.
apply(myBootstrap$t,2,sd)## 0.07573983 0.10295571 0.02726414különböző típusú bootstrap CIs
mielőtt elkezdenénk a CI-t, mindig érdemes egy pillantást vetni a bootstrap megvalósítások terjesztésére. Használhatjuk a plot függvényt, aindex megmondja, hogy a foo – ben kiszámított statisztikák közül melyiket kívánjuk megnézni. Itt a index=1 a Spearman korrelációs együtthatója az epális hossz és szélesség között, index=2 az OD sepal hosszának mediánja, ésindex=3az OD sepal szélességének mediánja.
plot(myBootstrap, index=1)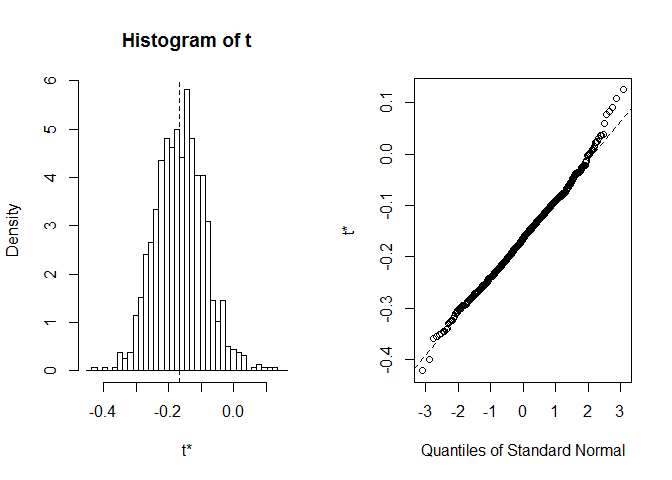
a bootstrap korrelációs együtthatók eloszlása elégnormálszerű. Keressük meg a CI-t. Használhatjuk boot.ci. Alapértelmezés szerint 95 százalékos CIs, de a conf paraméterrel módosítható.
boot.ci 5 típusú bootstrap CIs-t biztosít. Az egyik, a studentizedinterval egyedülálló. Meg kell becsülni a bootstrap varianciát. Nem adtuk meg, ezért a R figyelmeztetést nyomtat:bootstrap variances needed for studentized intervals. Varianceestimates lehet beszerezni a második szintű bootstrap vagy (könnyebb) withjackknife technika. Ez valahogy túlmutat ennek az oktatóanyagnak a keretein,ezért összpontosítsunk a bootstrap CIs fennmaradó négy típusára.
ha nem akarjuk mindet látni, kiválaszthatjuk a relevánsakat a type argumentumban. Lehetséges értékek norm, basic, stud, perc, bca ora vektor ezek.
a boot.ci függvény létrehozza az osztály objektumát… (igen, kitaláltad!)bootci. Elemeit ugyanúgy hívják, mint a typeargumentumban használt CI típusokat. A $norm egy 3 elemből álló vektor, amely konfidenciaszintű ci határokat tartalmaz.
boot.ci(myBootstrap, index=1, type='norm')$norm## conf ## 0.95 -0.3177714 -0.02087672$basic, $stud, $perc a $bca pedig 5 elemű Vektorok, amelyek tartalmazzák a CI kiszámításához használt percentiliseket is (erre később visszatérünk):
boot.ci(myBootstrap, index=1, type='basic')$basic## conf ## 0.95 975.98 25.03 -0.3211981 -0.03285178egy kis jelölés (sajnálom!)
ahhoz, hogy megértsük, mi a különböző típusú CI, be kell vezetnünknéhány jelölést. Szóval, hadd:
- t⋆ a bootstrap becslés (mármint a bootstraprealizations),
- t0 egy értéket a statisztika az eredeti adatállomány
- se⋆ egy standard hiba a bootstrap becslés,
- b lehet, hogy elfogultság, a bootstrap estimateb = t⋆ − t0
- α egy bizalmi szint, általában α = 0.95,
- za egy $1-\frac \alfa-2$-quantile of standardnormal engedély,
- θα egy α-százalékos eloszlása bootstraprealizations.
percentilis CI
a fenti jelöléssel a percentilis CI:
tehát ez csak releváns percentiliseket igényel. Semmi több.
normál CI
egy tipikus Wald CI a következő lenne:
de bootstrap esetben ki kell javítanunk az elfogultságot. Így válik:
$$ t_0 – b \pm z_\alpha \cdot se^\star \\2t_0-t^\star \pm z_\alpha \cdot se^\star$$
Basic ci
a percentilis CI általában nem ajánlott, mert rosszul teljesít, amikor furcsa farkú eloszlásokról van szó. Az alapvető CI (más néven pivotal vagy empirikus CI) sokkal robusztusabb ehhez. Az ésszerűség az, hogy kiszámoljuk a különbségeket az egyes bootstrap replikációk és t0 között, és felhasználjuk az eloszlásuk percentiliseit. L. Wasserman Allstatisztikájában
az alapvető CI végső képlete a következő:
BCa ci
a BCa torzítással korrigált, gyorsított. A képletmert nem túl bonyolult, de kissé értelmetlen, ezért kihagyom.Lásd Thomas J cikkét. Dicicio és BradleyEfron, ha érdeklik a részletek.
a metódus nevében említett gyorsítás megköveteli a bootstrap megvalósítások specifikus százalékainak használatát. Néha előfordulhat, hogyezek extrém százalékok lennének, esetleg kiugró értékek.A BCa ilyen esetekben instabil lehet.
nézzük meg a BCA CI-t a szirom szélességének mediánjára. Az eredeti adatkészletben ez a medián pontosan megegyezik 3.
BCa CI-t kapunk (2,9, 2,9). Ez furcsa, de szerencsére Rfigyelmeztetett minket, hogy extreme order statistics used as endpoints. Lássuk, mi történt pontosan itt:
plot(myBootstrap, index=3)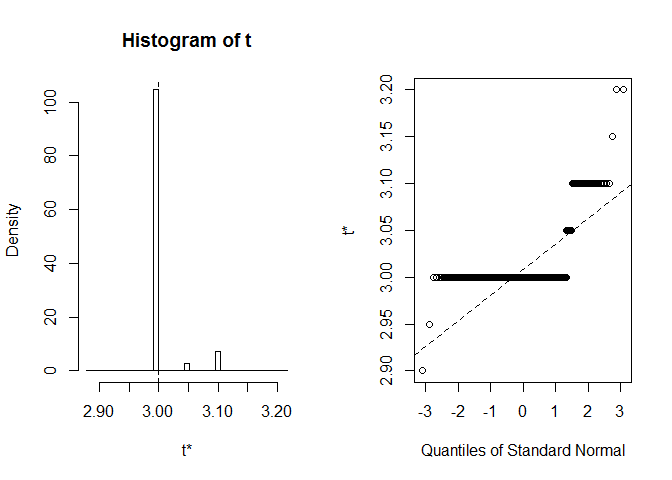
a bootstrap megvalósítások eloszlása szokatlan. Túlnyomó többségük (több mint 90%) 3S.
table(myBootstrap$t)#### 2.9 2.95 3 3.05 3.1 3.15 3.2## 1 1 908 24 63 1 2az eredmények replikációja
néha újra kell hoznunk a bootstrap replikációkat. Ha tudjuk használni R érte, ez nem jelent problémát. set.seed funkció megoldja a problémát.A bootstrap replikációk újrateremtése más szoftverekben sokkal többnehéz. Mi több, nagy R esetén az újraszámítás R – ban szintén nem lehet opció (például időhiány miatt).
tudjuk kezelni ezt a problémát, megtakarítás indexek elemeinek originaldataset, hogy kialakult minden bootstrap minta. Ezt teszi a boot.array függvény (indices=T argumentummal).
tableOfIndices<-boot.array(myBootstrap, indices=T)minden sor egy bootstrap minta. Eg., az első mintánk a következő elemeket tartalmazza:
Beállítás indices=F(alapértelmezett), választ kapunk a ” Howmany ahányszor az eredeti adatkészlet minden eleme megjelent az egyes bootstrapsample-ben?”. Például az első mintában: az adatkészlet 1. eleme megjelentegyszer, a 2. elem egyáltalán nem jelent meg, a 3.elem egyszer, 4. kétszer jelent meg stb.
egy ilyen táblázat lehetővé teszi számunkra, hogy újra bootstrap megvalósítás kívül R.Vagy magában a R – ban, amikor nem akarjuk használni a set.seed – et, és még egyszer elvégezni az összes számítást.
onceAgain<-apply(tableOfIndices, 1, foo, data=iris, cor.type='s')ellenőrizzük, hogy az eredmények megegyeznek-e:
Igen, vannak!
Ha többet szeretne megtudni a gépi tanulásról az R-ben, vegye be a DataCamp Machine Learning Toolbox tanfolyamát.