Egy kör egyenletesen oszlik hat egyenlő háromszögre

Szia Marilynn,

először elmondom a feltételezéseimet arról, hogy néz ki a képed:

1. minden háromszögnek van egy csúcsa (sarok) a kör közepén
2. minden háromszögnek sarkai vannak a kör kerületén (tehát minden háromszög két oldala sugár)
3. a háromszögek megosztják az oldalakat (a háromszögek között nincsenek gapes)

az összkép úgy néz ki, mint egy virág – minden háromszög egy szirom.

az ismeretlen terület az, ami a kör külső része körül marad, az egyes háromszögek kerülete és külső oldala között. Ez az ismeretlen terület hat egybevágó szakaszra oszlik (minden szempontból egyenlő – mint a háromszögek minden szempontból “egyenlőek” – beleértve a területet, az oldal hosszát és az ív hosszát). Nem világos, hogy egy ív területe Pi (valójában nem osztott pite, bár ugyanaz), vagy mind a hat szakasz együttvéve Pi. A következőkben feltételezem, hogy az egyik külső szakasz területe Pi, így mind a hat szakasz területe együttvéve 6-szor Pi. Meg kell találnunk A kör sugarát, nevezzük r.

a P-t is használom a Pi (vagy kb. 3.14). Most van egy csomó információ, amit a háromszögekből díszíthetünk:

1. a középpontban lévő szögek mind 60 fok. Ez azért van, mert a középpontban lévő hat szög egyenlő, és egy kör 360 fokos. Tehát 360 edivided által 6.
2. minden háromszög Egyenlő szárú. Ennek oka az, hogy két oldal egyenlő (az oldalak, amelyek sugara).
3. minden háromszög valójában egyenlő oldalú. Mivel ez iscoceles, a két külső szög is egyenlő. De egy háromszögben 180 fok van, a középső szögben már 60-at használnak, így a külső szögeknél 180-60=120 fok marad. De 120 osztva 2-vel 60 fok, tehát mindhárom szög egyenlő,tehát egyenlő.
4. minden háromszög minden oldala r hosszúságú. Ez azért van, mert 6 egybevágó (minden szempontból”egyenlő”) egyenlő oldalú háromszögünk van, és mert minden háromszög két oldala sugár.

a háromszögek geometriájából néhány algebrát kell tennünk. Mivel ismerünk egy területet, és szükségünk van egy sugárra, szükségünk van egy képletre (vagy egyenletre) a sugárra a terület szempontjából (a következőkben tartsuk szem előtt a képlet célját). A kör területe P * r2 (r2 azt jelenti, hogy R négyzet, * pedig szorzást jelent) a maradék szakaszok területe a háromszögeken kívül, de a körön belül (egy olyan terület, amelyet már nem 6*P), a háromszögek területének kivonásával is megtalálható a kör területéről. Meg kell találnunk az egyik egyenlő oldalú háromszög területét.

1. módszer háromszög területének kiszámításához
a háromszög területe b * h/2 Itt van szükség valamilyen trigonometriára: húzzon egy vonalat a csúcstól az ellenkező oldalra, amely az ellenkező oldalt kettéosztja, és derékszögben van. Ez az egyenlő oldalú háromszöget két egybevágó derékszögű háromszögre osztja, az új oldal pedig a magasság, nevezzük h. meg kell találnunk h.

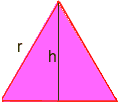
a trig használatával az egyik derékszögű háromszögben sin60 = h / r van, de sin60 = sqr (3) / 2, ahol sqr(3) három négyzetgyökét jelenti, tehát sqr(3)/2 = h/r szorozzuk meg mindkét oldalt r-vel, hogy h = r*sqr (3) / 2 r most egy egyenlő oldalú háromszög területe b*h/2 = (r)*(r*sqr(3)/2)/2 = (r2) * sqr(3)/4 r = sqr(6*P/(P-6*sqr (3)/4)) Használja a műveletek sorrendjét a számológépen történő kiszámításához (P=3,14): r= 5,896… Tehát a kör sugara kb. 5.9. Pál