különbség az IIR és a FIR szűrők között: a practical design guide
a digitális szűrő egy matematikai algoritmus, amely digitális adatkészleten (pl. szenzoradatokon) működik annak érdekében, hogy kinyerje az érdekes információkat és eltávolítsa a nem kívánt információkat. Az ilyen típusú technológiák alkalmazása magában foglalja a hibák eltávolítását az érzékelő adataiból, vagy akár a mért jel zajának tisztítását a könnyebb Adatelemzés érdekében. De hogyan válasszuk ki a legjobb típusú digitális szűrőt alkalmazásunkhoz? És mi a különbség az IIR szűrő és a FIR szűrő között?
a digitális szűrők a következő két kategóriába sorolhatók:
- végtelen impulzus válasz (IIR)
- véges impulzus válasz (FIR)
ahogy a nevek is sugallják, az egyes szűrőtípusokat az impulzusválasz hossza szerint kategorizálják. Mielőtt azonban részletes matematikai elemzéssel kezdenénk, érdemes felmérni az egyes szűrőtípusok teljesítményének és jellemzőinek különbségeit.
példa
az IIR és a FIR közötti különbségek szemléltetésére a 14.rendű FIR (folytonos vonal) és a 4. rendű Csebisev Iiir típusú (szaggatott vonal) frekvenciaválaszát az alábbi ábra mutatja 1. Figyeljük meg, hogy bár a magnitúdó spektrumok hasonló mértékű csillapítással rendelkeznek, az IIR szűrő fázisspektruma nemlineáris a passbandban (\(\small 0\rightarrow7.5Hz\)), és nagyon nemlineárisvá válik a cut-off frekvencián, \(\small f_c=7.5 Hz\). Vegye figyelembe azt is, hogy a FIR nagyobb számú együtthatót igényel (15 vs az IIR 10), hogy megfeleljen az IIR csillapítási jellemzőinek.
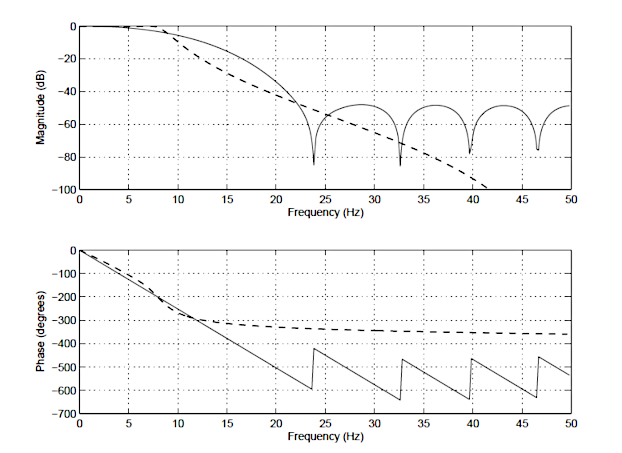
Ez csak néhány a különbség a két típusú szűrőket. Részletes összefoglaló a főbb előnyök, hátrányok minden típusú szűrő most követni.
IIR szűrők
az IIR (infinite impulse response) szűrőket általában olyan alkalmazásokhoz választják, ahol a lineáris fázis nem túl fontos és a memória korlátozott. Ők már széles körben elterjedt az audio kiegyenlítési, orvosbiológiai érzékelő jel feldolgozás, Sok/IIoT intelligens szenzorok, illetve a nagy sebességű távközlési/RF alkalmazások.
Előnyei
- Alacsony végrehajtási költség: kevesebb együtthatót és memóriát igényel, mint a FIR szűrők, hogy megfeleljenek egy hasonló specifikációnak, azaz a cut-off frekvenciának és a stopband csillapításnak.
- alacsony késleltetés: alkalmas valós idejű vezérlésre és nagyon nagy sebességű RF alkalmazásokra az együtthatók alacsony száma miatt.
- Analóg egyenértékű: használható az analóg szűrők jellemzőinek utánzására s-z síktérképezési transzformációk segítségével.
hátrányok
- nemlineáris fázis jellemzői: Az IIR szűrő fázisjellemzői általában nemlineárisak, különösen a levágási frekvenciák közelében. All-pass kiegyenlítő szűrőket lehet használni annak érdekében, hogy javítsa a passband fázis jellemzőit.
- részletesebb elemzés: több skálázást és numerikus túlcsordulási elemzést igényel, ha rögzített pontban hajtják végre. A Direct form II szűrőszerkezet különösen érzékeny a kvantálás hatásaira, és a tervezési fázisban különös gondosságot igényel.
- numerikus stabilitás: Számszerűen kevésbé stabil, mint FIR (véges impulzusválasz) társaik, a visszacsatolási utak miatt.
FIR szűrők
a FIR (véges impulzus válasz) szűrőket általában olyan alkalmazásokhoz választják, ahol a lineáris fázis fontos, és megfelelő mennyiségű memória és számítási teljesítmény áll rendelkezésre. Széles körben alkalmazzák az audio és Orvosbiológiai jeljavító alkalmazásokban. Teljesen nulla szerkezetük (az alábbiakban tárgyaljuk) biztosítja, hogy soha ne váljanak instabillá semmilyen típusú bemeneti jelnél, ami egyértelmű előnyt jelent számukra az IIR-rel szemben.
előnyök
- lineáris fázis: a fenyők könnyen megtervezhetők lineáris fázisra. Ez azt jelenti, hogy a szűrendő jelbe nem kerül fázistorzítás, mivel az összes frekvencia időben azonos mértékben eltolódik – így megtartva relatív harmonikus kapcsolataikat (azaz állandó csoport és fáziskésés). Ez természetesen nem vonatkozik az IIR szűrőkre, amelyek nemlineáris fázisjellemzővel rendelkeznek.
- stabilitás: mivel a FIRs nem használja a korábbi kimeneti értékeket a jelenlegi kimenet kiszámításához, azaz. nincs visszajelzésük, soha nem válhatnak instabillá bármilyen típusú bemeneti jel esetén, ami egyértelmű előnyt jelent számukra az IIR szűrőkkel szemben.
- tetszőleges frekvenciaválasz: a Parks-McClellan és az ASN FilterScript firarb() függvénye lehetővé teszi egy tetszőleges magnitúdójú FIR kialakítását. Ez azt jelenti, hogy a FIR könnyebben testreszabható, mint az IIR.
- fixpontos teljesítmény: a kvantálás hatásai kevésbé súlyosak, mint az IIR hatásai.
hátrányok
- magas számítási és memóriaigény: A fenyők általában sokkal több együtthatót igényelnek az éles határérték eléréséhez, mint az IIR társaik. Ennek az a következménye, hogy sokkal több memóriát és jelentősen nagyobb mennyiségű MAC (többszörös és felhalmozódó) műveletet igényelnek. Az Arm Cortex-M magjain alapuló modern mikrovezérlő architektúrák azonban ma már tartalmazzák a DSP hardveres támogatását a SIMD (signal instruction, multiple data) segítségével, amelyek jelentősen felgyorsítják a szűrési műveletet.
- magasabb késleltetés: a nagyobb együtthatók száma azt jelenti, hogy általában egy FIR kevésbé alkalmas, mint egy IIR gyors, nagy áteresztőképességű alkalmazásokhoz. Ez problematikussá válik a valós idejű zárt hurkú vezérlő alkalmazásoknál, ahol a FIR szűrőnek túl sok Csoportos késleltetése lehet a hurok stabilitásának eléréséhez.
- nincs analóg egyenértékű: a bilineáris, illesztett z-transzformáció (s-z leképezés) segítségével az analóg szűrő könnyen átalakítható ekvivalens IIR szűrővé. Ez azonban nem lehetséges egy FIR esetében, mivel nincs analóg megfelelője.
matematikai meghatározások
amint azt a bevezetőben tárgyaltuk, az IIR és a FIR név az egyes szűrőtípusok matematikai meghatározásaiból származik, azaz az IIR szűrőt elméletileg végtelen impulzusválasz alapján kategorizálják,
y (n)=\sum_{k=0}^{\infty}h (k)x (n-k)
\)
és a véges impulzusválasz alapján kategorizált FIR,
y (n)=\sum_{k=0}^{N-1}h (k)x (n-k)
\)
most elemezzük az egyes szűrőtípusok matematikai tulajdonságait.
IIR definíció
mint fent látható, az IIR szűrőt elméletileg végtelen impulzusválasza alapján kategorizálják,
\(\displaystyle y (n)=\sum_{k=0}^{\infty}h(k) x(n-k)\)
gyakorlatilag nem lehet kiszámítani az IIR kimenetét ezen egyenlet segítségével. Ezért az egyenlet újraírható véges számú pólus \(\kis p\) és nullák \(\kis q\) szerint, amelyet a lineáris állandó együttható különbség egyenlete határoz meg:
y(n)= \ sum_{k=0}^{q}b_k x (n-k)- \ sum_{k=1}^{p}a_ky (n-k)
\)
ahol \(\small a_k\) és \(\small b_k\) a szűrő nevező és számláló polinom együtthatói, akik gyökerei megegyeznek a szűrő pólusaival és nulláival. Így tehát a különbségegyenlet és a Z-transzformáció (átviteli függvény) közötti kapcsolat meghatározható a z-transzformáció késleltetési tulajdonságának felhasználásával úgy, hogy,
\sum_{k=0}^{q}b_kx(n-k)-\sum_{k=1}^{p}a_ky(n-k)\quad\stackrel{\displaystyle\mathcal{Z}}{\longleftrightarrow}\quad\frac{\sum\limits_{k=0}^q b_kz^{- k}}{1 + \ sum \ limits_{k=1}^p a_kz^{- k}}
\)
mint látható, az átviteli függvény a szűrő frekvenciatartományának ábrázolása. Vegye figyelembe azt is, hogy a pólusok a kimeneti adatokra, a nullák pedig a bemeneti adatokra hatnak. Mivel a pólusok a kimeneti adatokra hatnak, és befolyásolják a stabilitást, elengedhetetlen, hogy sugaraik az egységkörön belül maradjanak (azaz <1) a BIBO (korlátozott bemenet, korlátozott kimenet) stabilitásához. A nullák sugara kevésbé kritikus, mivel nem befolyásolják a szűrő stabilitását. Ez az elsődleges oka annak, hogy az összes nulla FIR (véges impulzusválasz) szűrők mindig stabilak.
BIBO stabilitás
egy lineáris időinvariáns (lti) rendszer (mint például egy digitális szűrő) korlátos bemenet, korlátos kimenet stabil, vagy BIBO stabil, ha minden korlátos bemenet korlátos kimenetet eredményez, mint
\(\displaystyle \sum_{k=0}^{\infty}\left|h(k)\right|<\infty \)
ahol \(\kis h(k)\) az LTI rendszer impulzusválasza. Ezt az egyenletet elemezve egyértelműnek kell lennie, hogy a BIBO stabilitási kritérium csak akkor teljesül, ha a rendszer pólusai az egységkörön belül helyezkednek el, mivel a rendszer ROC-jának (konvergencia régiójának) tartalmaznia kell az egységkört. Következésképpen elegendő azt mondani, hogy egy korlátozott bemeneti jel mindig korlátozott kimeneti jelet fog előállítani, ha az összes pólus az egység körén belül fekszik.
a nullákat viszont nem korlátozza ez a követelmény, és ennek következtében bárhol a z-síkon feküdhetnek, mivel közvetlenül nem befolyásolják a rendszer stabilitását. Ezért a rendszerstabilitási elemzés elvégezhető úgy, hogy először kiszámítjuk az átviteli függvény gyökereit (azaz a számláló és nevező polinomok gyökereit), majd a megfelelő pólusokat és nullákat a z-síkra rajzoljuk.
érdekes helyzet áll elő, ha bármelyik pólus az egységkörön fekszik, mivel a rendszerről azt mondják, hogy csekély mértékben stabil, mivel sem stabil, sem instabil. Bár a marginálisan stabil rendszerek nem BIBO stabilak, a digitális oszcillátorok tervezői kihasználták őket, mivel impulzusválaszuk egyszerű módszert kínál a szinuszhullámok generálására, amelyek felbecsülhetetlen értékűnek bizonyultak a távközlés területén.
Biquad IIR szűrők
az itt tárgyalt IIR szűrő implementáció biquad, mivel két pólusa és két nullája van, amint azt az alábbi 2.ábra szemlélteti. A biquad implementáció különösen hasznos a fixpontos implementációknál, mivel a kvantálás és a numerikus stabilitás hatása minimálisra csökken. Bármely biquad megvalósítás általános sikere azonban a rendelkezésre álló számpontosságtól függ, amelynek elegendőnek kell lennie ahhoz, hogy a kvantált pólusok mindig az egységkörön belül legyenek.
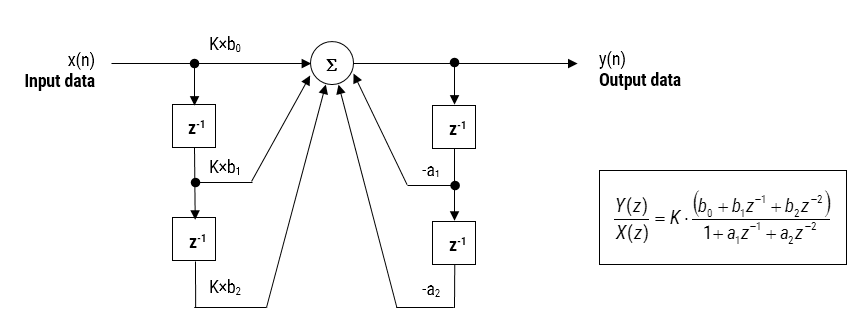
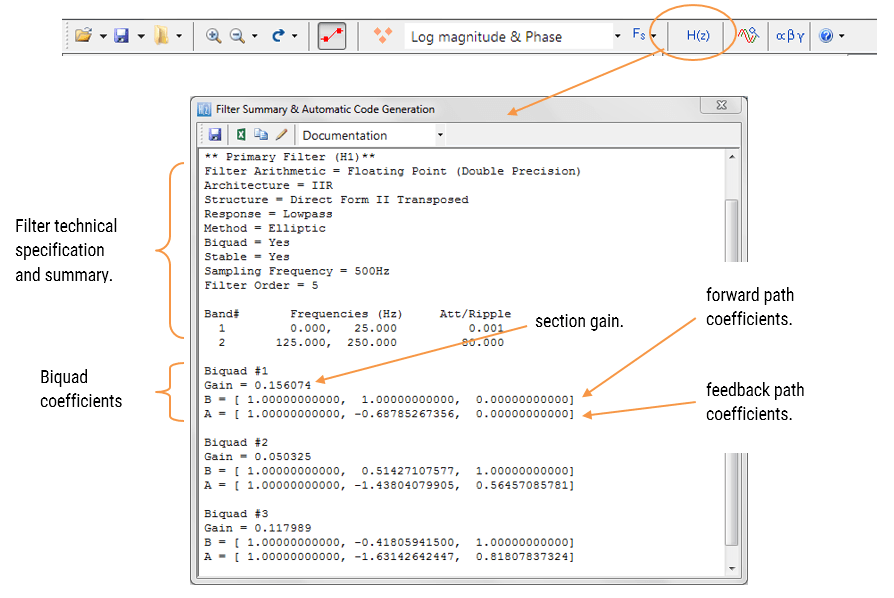
2. ábra: közvetlen forma I (biquad) IIR szűrő megvalósítása és átviteli funkció.
a 2. ábrát elemezve látható, hogy a biquad struktúra valójában két visszacsatolási útvonalból áll (\(\small a_1\) és \(\small a_2\)), három előremeneti útvonalból (\(\small b_0, b_1\) és \(\small b_2\)) és egy szakaszerősítésből, \(\small K\). Így az 1. ábra szűrési művelete a következő egyszerű rekurzív egyenlettel foglalható össze:
\(\displaystyle y (n)=k \ szor \ nagy – a_1 y(n-1) – a_2 y (n-2)\)
elemezve az egyenletet, vegye figyelembe, hogy a biquad implementáció csak négy kiegészítést igényel (csak egy akkumulátort igényel) és öt szorzást, amelyek könnyen elhelyezhetők bármely Cortex-M mikrovezérlőn. A szakasz nyeresége, \ (\kis k\) a megvalósítás előtt előre megszorozható az előremenő út együtthatóival is.
a Biquad szűrők gyűjteményét Biquad kaszkádnak nevezzük, amint azt az alábbiakban szemléltetjük.

az ASN Filter Designer akár 50 biquadot is képes megtervezni és megvalósítani (csak Professional edition).
lebegőpontos megvalósítás
ha egy szűrőt lebegőpontos (azaz kettős vagy egyetlen pontosságú aritmetikát használó) direct Form II struktúrák jobb választásnak tekinthetők, mint a Direct Form I struktúra. A direct Form II transzponált struktúrát tekintik a legpontosabbnak numerikusan lebegőpontos megvalósítás, mivel a numerikus swamping nemkívánatos hatásait minimalizálják, amint az a különbségegyenletek elemzésével látható.
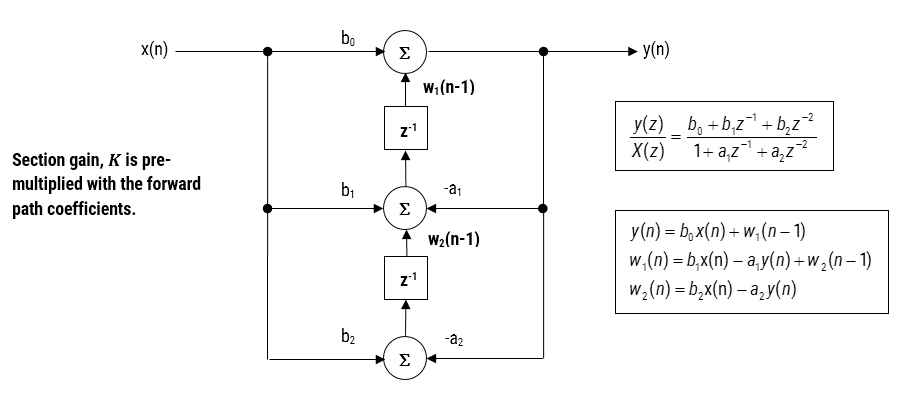
3. ábra-Direct Form II átültetett strucutre, transfer function and difference equations
a szűrő összefoglaló (ábrán látható 4) nyújt a tervező részletes áttekintést a tervezett szűrő, beleértve a részletes összefoglalót a műszaki előírások és a szűrő együtthatók, amely bemutatja a gyors és egyszerű útvonal dokumentálása a design.
az ASN Filter Designer támogatja mind az egyszakaszos, mind a Biquad (alapértelmezett beállítás) IIR szűrők tervezését és megvalósítását.
FIR definíció
az IIR lineáris állandó együttható-különbség egyenletének visszaadása, azaz
y(n)=\sum_{k=0}^{q}b_kx(n-k)-\sum_{k=1}^{p}a_ky (n-k)
\)
figyeljük meg, hogy amikor a \(\small a_k\) együtthatókat (azaz a visszacsatolást) nullára állítjuk, a definíció az eredeti FIR szűrődefiníciónkra redukálódik, ami azt jelenti, hogy a FIR számítás csak a múltbeli és a jelenlegi bemeneti értékeken alapul, nevezetesen:
y (n) = \ sum_{k=0}^{q}b_kx (n-k)
\)
implementáció
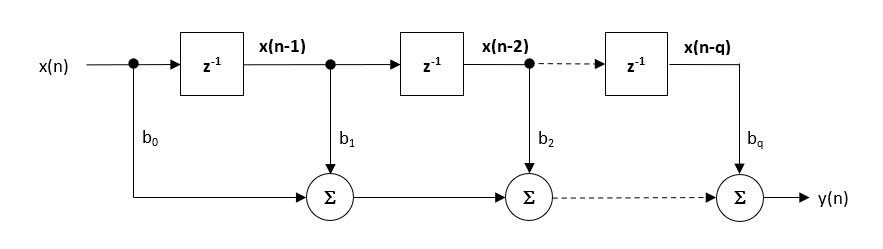
bár számos gyakorlati megvalósítás létezik a FIRs számára, a közvetlen alakstruktúra és annak átültetett unokatestvére talán a leggyakrabban használt, és mint ilyen, az összes tervezett szűrő együtthatót közvetlen alakstruktúrában való megvalósításra szánják.
a közvetlen alakszerkezet és a kapcsolódó különbségegyenlet az alábbiakban látható. A közvetlen formát az egyetlen akkumulátor koncepció alapján a fix pont megvalósítására támogatják.
\(\displaystyle y(n) = b_0x(n) + b_1x(n-1) + b_2x(n-2)+…. +b_qx (n-q) \)
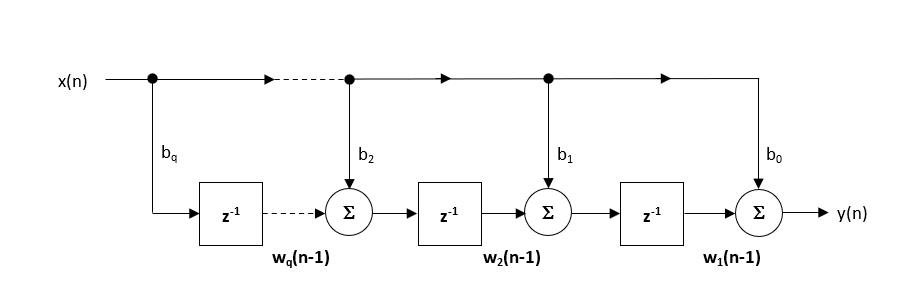
az ASN Szűrőtervezőn belül az ajánlott (alapértelmezett) struktúra a Direct Form Transponed structure, mivel ez kiváló numerikus pontosságot kínál lebegőpontos aritmetika használatakor. Ez könnyen látható az alábbi (a megvalósításhoz használt) különbségegyenletek elemzésével, mivel a numerikus swamping nemkívánatos hatásai minimalizálódnak, mivel a lebegőpontos összeadást hasonló nagyságrendű számokon hajtják végre.
\(\displaystyle \begin{eqnarray}y(n) & = &b_0x(n) &+& w_1(n-1) \\ w_1(n)&=&b_1x(n) &+& w_2(n-1) \\ w_2(n)&=&b_2x(n) &+& w_3(n-1) \\ \vdots\quad &=& \quad\vdots &+&\quad\vdots \\ w_q(n)&=&b_qx(n) \end{eqnarray}\)
mit tanultunk?
a digitális szűrők a következő két kategóriába sorolhatók:
- végtelen impulzus válasz (IIR)
- véges impulzus válasz (FIR)
az IIR (infinite impulse response) szűrőket általában olyan alkalmazásokhoz választják, ahol a lineáris fázis nem túl fontos és a memória korlátozott. Ők már széles körben elterjedt az audio kiegyenlítési, orvosbiológiai érzékelő jel feldolgozás, Sok/IIoT intelligens szenzorok, illetve a nagy sebességű távközlési/RF alkalmazások.
a FIR (véges impulzus válasz) szűrőket általában olyan alkalmazásokhoz választják, ahol a lineáris fázis fontos, és megfelelő mennyiségű memória és számítási teljesítmény áll rendelkezésre. Széles körben alkalmazzák az audio és Orvosbiológiai jeljavító alkalmazásokban.
az ASN Filter Designer mindent megad a mérnököknek, amire szükségük van a komplex IIR és FIR digitális szűrők tervezéséhez, kísérletezéséhez és telepítéséhez a különböző érzékelőmérési alkalmazásokhoz. Ezek az előnyök az automatikus dokumentációval és a kódgenerálási funkcióval párosulva lehetővé teszik a mérnökök számára, hogy az IIR/FIR digitális szűrőt órák helyett perceken belül tervezzék és érvényesítsék.
