KDnuggets

Írta: Sydney Firmin, Alteryx.

“lényegében minden modell rossz, de egyes modellek hasznosak.”- George Box

ezt a híres George Box idézetet először 1976-ban rögzítették a “Science and Statistics” című cikkben, amelyet a Journal of the American Statistical Association publikált. Fontos idézet a statisztika és az analitikai modellek területén, és két részből lehet kicsomagolni.

minden modell hibás

ahhoz, hogy ezt az állítást elmélyítsük, meg kell határoznunk és meg kell vizsgálnunk, hogy mi a modell.

e cikk kontextusában a modell egy rendszer vagy objektum egyszerűsített ábrázolásának tekinthető. A statisztikai modellek megközelítik az adathalmaz mintáit azáltal, hogy feltételezéseket tesznek az adatokról, valamint a környezetről, amelyben összegyűjtötték és alkalmazták.

a statisztikai modellek feltételezéseinek három tág kategóriája a disztribúciós feltételezések (feltételezések az értékek eloszlásáról egy változóban vagy a megfigyelési hibák eloszlása), strukturális feltételezések (feltételezések a változók közötti funkcionális kapcsolatról) és keresztváltozási feltételezések (közös valószínűségi eloszlás).

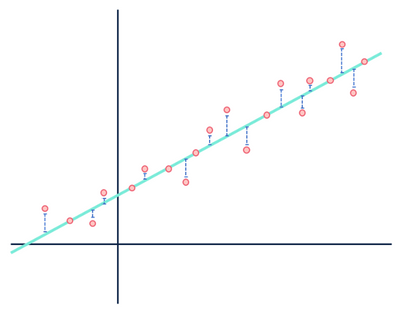
például egy lineáris regressziós modell feltételezi, hogy az adathalmaz változói közötti kapcsolatok lineárisak (és csak lineárisak). Egy lineáris modell szemében az adathalmazt alkotó megfigyelések és a modellezett vonal közötti távolság csak zaj (azaz az adatok véletlenszerű vagy megmagyarázhatatlan ingadozása), és végül figyelmen kívül hagyható.

ne törődj a kék távolságokkal.

George Box kijelentette, hogy minden modell téves, kifejezetten a statisztikai modellek összefüggésében. Mivel a modell természete valaminek egyszerűsített és idealizált ábrázolása, bizonyos értelemben minden modell hibás lesz. A modellek soha nem lesznek “az igazság”, ha az igazság azt jelenti, hogy a valóság teljesen reprezentatív. Nagyon fontos figyelembe venni a modell generálásakor tett feltételezéseket, mert a modellek csak akkor igazán hasznosak, ha a feltételezéseket feltartják.

Térképek és miniatúrák

Box “minden modell hibás” – jéhez hasonló megfigyelések sok különböző területen vannak jelen.

van egy aforizma, amely a térkép-terület viszonyra utal, amelyet Alfred Korzybskinek tulajdonítanak:

a térkép nem az a terület, amelyet képvisel, de ha helyes, akkor hasonló szerkezetű, mint a terület, amely figyelembe veszi annak hasznosságát.

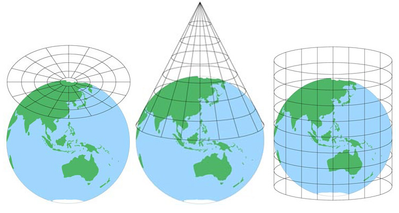
a térképek azért hasznosak, mert egy valós objektum absztrakciói egy kezelhetőbb skálán, de mindig kizárnak valamilyen részletességet. Attól függően, hogy a térkép mekkora területet tartalmaz, a térkép vetülete miatt némi torzulás is előfordulhat (amelyet a gömb alakú földgömb lapos ábrázolássá történő átalakításának trükkös folyamata okoz).

(kép forrása.)

az egyetlen igazán pontos térkép az általa képviselt Terület 1: 1 arányú replikációja lenne. Egy ilyen térkép azonban nem lenne hasznosabb, mint maga a terület navigálása.

fontolja meg Paul Valery költő idézetét:

minden egyszerű hamis. Minden, ami összetett, használhatatlan.

a Stanford üzleti professzoráról elnevezett Bonini-paradoxon leírja a komplex rendszerek hasznos, teljes modelljeinek vagy szimulációinak létrehozásának kihívását. A modellfejlesztés során gyakran van egyensúly a komplexitás és a pontosság között. Ha egy modell célja egy kapcsolat vagy rendszer világosabbá tétele, a hozzáadott komplexitás legyőzi ezt a célt (bár ez pontosabbá teheti a modellt).

magas szinten a térkép-terület reláció leírja az objektum és az objektum ábrázolása közötti kapcsolatot is.

ha valaha is részt vett filozófiaórán, akkor találkozhatott Rene Magritte szürrealista művész képek árulása című művével.

a szöveg fordítása: “ez nem cső.”És nem az. Ezt a (digitális) képet nem tömhetjük dohányba, és nem szívhatjuk el, mivel ez csak egy valós tárgy ábrázolása.

a modellek absztrakciók. A térképekhez, miniatűr építészeti modellekhez vagy vázlatokhoz hasonlóan nem képesek megragadni az objektum vagy rendszer minden részletét, amelyre épülnek, már csak azért is, mert nem léteznek a valós világban, és nem ugyanúgy működnek.

Ha Minden Modell Rossz, Miért Zavarja?

George Box aforizmája nem nélkülözi kritikusait.

úgy tűnik, hogy sok statisztikus problémája ezzel az idézettel nagyjából két kategóriába sorolható:

1. a modellek tévedése nyilvánvaló állítás. Természetesen minden modell téved, ők modellek.
2. ez az idézet ürügyként szolgál a rossz modellek számára.

J. Michael Steele statisztikus kritizálta a mondást (lásd ezt a személyes esszét). Steele elsődleges érve az, hogy a “rossz” csak akkor jön szóba, ha a modell nem válaszol helyesen arra a kérdésre, amelyre állítása szerint válaszol (pl., hogy a térképen lévő épületet rosszul címkézik, nem pedig azt, hogy az épületet egy kis négyzet képviseli). Steele megy az állami:

a közzétett statisztikai módszerek többsége éhezik egy őszinte példára.

Steele azzal érvel, hogy a statisztikai modellek gyakran nem felelnek meg a megfelelő alkalmassági mutatóknak, és a statisztikusok által kifejlesztett számos modell nem elegendő a tervezett felhasználási esetekhez.

a cikkben a statisztika mint tudomány, nem művészet: A túlélés módja az Adattudományban, Mark Van der Laan (a UC Berkeley statisztikája) a dobozos idézetet a rossz statisztikai modellek hozzájáruló okának tulajdonítja, és elutasítja, mint “teljes ostobaságot.”Tovább ír:

a statisztika alapja ( … ) nem lehetett önkényesen kiválasztani egy “kényelmes” statisztikai modellt. A legtöbb statisztikus azonban pontosan ezt teszi, büszkén hivatkozva az idézetre: “minden modell rossz, de néhány hasznos.”Emiatt azok a modellek, amelyek annyira irreálisak, hogy egy véges dimenziós paraméter indexeli őket, még mindig a status quo, annak ellenére, hogy mindenki egyetért azzal, hogy hamisak.

megoldásként Van der Laan felszólítja a statisztikusokat, hogy hagyják abba Box idézetét, és vállalják, hogy komolyan veszik az adatokat, a statisztikákat és a tudományos módszert. Felhívja a statisztikusokat, hogy töltsenek időt azzal, hogy megtanulják, hogyan keletkeztek egy adott adathalmaz adatai, és vállalják, hogy reális statisztikai modelleket dolgoznak ki gépi tanulás és adat adaptív becslési technikák alkalmazásával a hagyományosabb paraméteres modellek helyett.

ez a cikk Michael Lavine és Christopher Tong statisztikusok válaszait, valamint az eredeti szerző válaszait tartalmazza. A két megcáfoló statisztikus olyan példákra mutat, ahol a modellek köztudottan tévesek, de gyakran alkalmazzák őket, mert hasznosak és alkalmasak egy adott problémára. Példáik közé tartozik az optika területén található három különböző fénymodell (geometriai optika, fizikai optika és kvantumoptika; mindhárom modell másképp képviseli a fényt, bizonyos értelemben “rossz”, és még ma is alkalmazzák), valamint a Szénáram naplója és a talaj hőmérséklete közötti (majdnem) lineáris kapcsolat a Harvard-erdőben gyűjtött adatokban.

viszont Van der Laan reagál ezekre a példákra és a cikk egyéb kritikáira, különösen az “igazi” modell megtalálásának koncepciójára. A válasz leveleket mindenképpen érdemes elolvasni, ha érdekel. Ez egy aktív vitaterület a statisztika és az Adattudomány területén.

de néhány modell hasznos

a modellek korlátai ellenére sok modell nagyon hasznos lehet. Mivel egyszerűsítettek, a modellek gyakran hasznosak a rendszer egy bizonyos összetevőjének vagy aspektusának megértésében.

az Adattudomány összefüggésében a gépi tanulás és a statisztikai modellek hasznosak lehetnek az ismeretlen értékek becsléséhez (előrejelzéséhez). Sok összefüggésben, ha a modell feltételezései megállják a helyüket, az erős statisztikai modell által adott bizonytalan becslés továbbra is nagyon hasznos lehet a döntések meghozatalában.

George Box bölcsességének második, kevésbé idézett fele ez:

“a gyakorlati kérdés az, hogy mennyire rossznak kell lennie (modellek), hogy ne legyenek hasznosak.”- George Box

vessünk egy pillantást a lineáris regressziós példánkra:

többnyire túl sok időt töltöttem ezen a képen, hogy csak egyszer használjam.

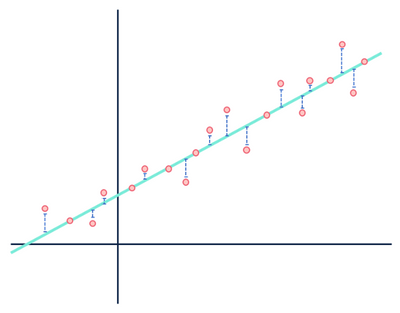
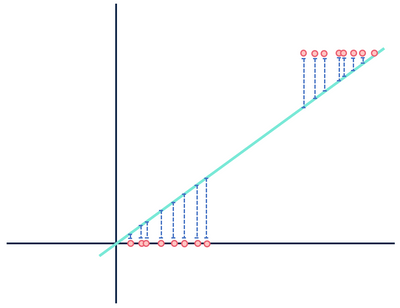
most vessünk egy pillantást egy másik elméleti lineáris regressziós modellre, amely illeszkedik egy másik adatkészlethez.

ne törődj a távolságokkal … várj, ez nem lehet helyes.

mindkét ábra hibát mutat, de az egyik adatkészlet egyértelműen lineáris kapcsolatot mutat, míg a másik logisztikai. Mindkét modell “rossz”, de az egyik egyértelműen rögzíti a változók közötti valós kapcsolatot, míg a másik nem, így az egyik hasznos, a másik haszontalan. A távolságok kék színnel történő elvetése zajként ésszerű, ha az adatok lineáris kapcsolatban állnak, de ez a feltételezés szétesik, ha a kapcsolat funkcionális alakja eltér a kiválasztott modelltől.

jó modellek készítése

az a tény, hogy a modellek tévesek vagy korlátozottak abban, amit képviselnek, sok ember számára nyilvánvalónak tűnhet, akik modellekkel dolgoznak, de sajnos sokan nem veszik észre, vagy sokat gondolkodnak rajta. Ezért érzem fontosnak, hogy George Box szavait szem előtt tartsuk a modell kidolgozásakor. Nem szabad ürügyként használni a rossz modellek felépítésére.

további olvasmányként Steele-nek van néhány nagyszerű osztályjegyzete: van-e értelme a modellnek? van értelme a modellnek? II. rész: a megfelelőség kihasználása. Egy másik nagyszerű forrás a ‘Minden modell rossz…’ című cikk: bevezetés a modell bizonytalanságába egy 2011-ben Groningenben tartott modellválasztó műhelyből.

egy másik érdekes olvasmány Az When All Models are Wrong from Issues in Science and Technology, amely Box szavaira hívja fel a tudományos és statisztikai modellek szigorúbb átláthatóságát.

az a fontos, hogy mindezt figyelembe vegye, hogy megértse, hogy az adatok mely aspektusait rögzíti a modell, és mely szempontokat nem. Fontos, hogy ellenőrizze a feltételezéseket és a kiindulási pontokat. Statisztikusként vagy adattudósként az Ön felelőssége, hogy szigorú modelleket készítsen, valamint ismerje azok korlátait. Mindig jelentse a bizonytalanságot, valamint a modell hatókörét. Ezt szem előtt tartva, akkor képes lesz arra, hogy a modellek, bár esetleg rossz, minden bizonnyal hasznos lehet.

eredeti. Újraküldve engedélyével.

Bio: A földrajztudós képzés és az adatok geek a szíve, Sydney szilárdan hiszi, hogy az adatok és a tudás a legértékesebb, ha lehet egyértelműen közölni és megérteni. A jelenlegi Sr. Data Science Content Engineer szerepében napjait azzal töltheti, amit a legjobban szeret: a technikai tudást és a kutatást vonzó, kreatív és szórakoztató tartalmakká alakítja az Alteryx közösség számára.

kapcsolódó:

• a 3 legnagyobb hiba az Adattudomány tanulásában
• 3 nagy probléma a nagy adatokkal és azok megoldásának módjával
• választás a Modelljelöltek között