logaritmusok használata a Való Világban

a logaritmusok mindenütt megtalálhatók. Használta már a következő kifejezéseket?

• 6 ábrák
• kétszámjegyű
• nagyságrendje
• kamatláb

a számokat a 10-es hatványuk alapján írja le, logaritmus. A kamatláb pedig a befektetés növekedésének logaritmusa.

meglepett, hogy a logaritmusok olyan gyakoriak? Én is. A legtöbb matematikai kísérlet a Való Világban (TM) rámutat a logaritmusokra valamilyen misztikus képletben, vagy úgy tesz, mintha geológusok lennénk, akiket lenyűgöz a Richter-skála. “A tudósok törődnek a rönkökkel, és neked is ezt kellene tenned. El tudsz képzelni egy világot cink nélkül?”

nem, nem, nem, nem, nem! (Mama mia!)

a matematika olyan fogalmakat fejez ki, mint az “ln” vagy a “napló”. A “matematika a Való Világban” megtalálása azt jelenti, hogy az életben találkozunk az ötletekkel, és megnézzük, hogyan lehet őket jelöléssel írni. Ne keresse a szó szerinti szimbólumokat! Mikor írtál utoljára hadosztálytáblát? Mikor vágtál fel utoljára ételt?

Ok, ok, értjük: miről szólnak a logaritmusok?

a logaritmusok megtalálják a hatás okát, azaz valamilyen kimenet bemenete

gyakori “hatás”, amikor valami növekszik, például 100 dollárról 150 dollárra megy 5 év alatt. Hogy történt ez? Nem vagyunk biztosak benne, de a logaritmus egy lehetséges okot talál: az LN(150/100) / 5 = 8,1% folyamatos visszatérése magyarázná ezt a változást. Lehet, hogy nem ez a tényleges ok (az összes növekedés az utolsó évben történt?), de ez egy sima átlag, amelyet összehasonlíthatunk más változásokkal.

egyébként az “ok-okozat” fogalma árnyalt. Miért nagyobb 1000, mint 100?

• 100 van 10 amely önmagában nőtt 2 időszakok ($10 * 10$)
• 1000 van 10 amely önmagában nőtt 3 időszakok ($10 * 10 * 10$)

a számokra úgy gondolhatunk, mint kimenetekre (1000 Az “1000 kimenet”) és bemenetekre (“hányszor kell 10-nek növekednie ahhoz, hogy ezek a kimenetek létrejöjjenek?”). Tehát,

1000 outputs > 100 outputs

mert

3 inputs > 2 inputs

vagy más szavakkal:

log(1000) > log(100)

miért hasznos ez?

a logaritmusok a számokat emberbarát skálán helyezik el.

nagy számok törik az agyunkat. Milliók és billiók “igazán nagyok” annak ellenére, hogy egy millió másodperc 12 nap, egy billió másodperc pedig 30 000 év. Ez a különbség egy amerikai nyaralási év és az egész emberi civilizáció között.

a “hatalmas számvakság” leküzdésének trükkje az, hogy számokat írunk “bemenetek” (azaz 10.teljesítménybázisuk) szempontjából. Ez a kisebb skála (0-100) sokkal könnyebben megfogható:

• teljesítmény 0 = $10^0$ = 1 (egyetlen elem)
• teljesítmény 1 = $10^1$ = 10
• teljesítmény 3 = $10^3$ = ezer
• teljesítmény 6 = $10^6$ = millió
• teljesítmény 9 = $10^9$ = milliárd
• teljesítmény 12 = $10^12$ = billió
• teljesítmény 23 = $10^23$ = molekulák száma Egy tucat gramm szénben
• teljesítmény 80 = $10^80$ = molekulák száma az univerzumban

a 0-80 skála elvitt minket egyetlen elemtől az univerzumban lévő dolgok számáig. Nem túl kopott.

a logaritmusok a szorzást lépésekként számolják

a logaritmusok a szorzás változásait írják le: a fenti példákban minden lépés 10x nagyobb. A természetes naplóval minden lépés “e” (2.71828…) alkalommal több.

amikor szorzások sorozatával foglalkozunk, a logaritmusok segítenek “megszámolni” őket, csakúgy, mint az összeadás számít nekünk, amikor effektusokat adunk hozzá.

mutasd meg a matekot

ideje a húsnak: lássuk, hol jelennek meg a logaritmusok!

hat számjegyű fizetés vagy 2 számjegyű költség

a számokat számjegyük szerint írjuk le, azaz. hány ereje van 10-nek (tíz, száz, ezer, tízezer stb.). Egy számjegy hozzáadása azt jelenti ,hogy” megszorozzuk 10-gyel”, azaz.

a logaritmusok megszámolják a hozzáadott szorzások számát, így 1-től kezdve (egyetlen számjegy) további 5 számjegyet ($10^5$) adunk hozzá, és 100 000 6 számjegyű eredményt kapunk. A “százezer” helyett a “6” – ról beszélünk a logaritmusok lényege. Durva skálaérzetet ad anélkül, hogy a részletekbe ugrana.

bónusz kérdés: hogyan írná le az 500 000-et? Mondván: “6 ábra” félrevezető, mert 6-számok gyakran azt jelenti, valami közelebb 100.000. A” 6,5-ös szám ” működni fog?

nem igazán. A fejünkben a 6,5 azt jelenti, hogy “félúton” 6 és 7 szám között, de ez egy összeadó gondolkodásmódja. Logaritmussal a”.5″: félúton a szorzás szempontjából, azaz a négyzetgyök ($9^.5$ azt jelenti, hogy a 9-3 négyzetgyöke félúton van a szorzás szempontjából, mert 1-3 és 3-9).

a naplót(500 000) véve 5,7-et kapunk, hozzáadunk 1-et az extra számjegyhez, és azt mondhatjuk, hogy ” 500 000 egy 6.7 ábra száma”. Próbálja ki itt:

nagyságrendje

mi geekek szeretjük ezt a kifejezést. Ez nagyjából “10x különbséget” jelent, de csak hűvösebbnek hangzik, mint az “1 számjegyű nagyobb”.

számítógépekben, ahol mindent bitekkel számolnak (1 vagy 0), minden bitnek duplázó hatása van (nem 10x). Tehát megy 8-16 bit “8 nagyságrenddel” vagy $2^8 = 256 $ – szor nagyobb. (A” nagyobb ” ebben az esetben a kezelhető memória mennyiségére utal.) 16-ról 32 bitre haladva további 16 nagyságrendet jelent, vagy 2^16 $ ~ 65 536-szor több memóriát lehet kezelni.

kamatlábak

Hogyan találjuk ki a növekedési rátákat? Egy ország nem szándékozik évi 8,56% – os növekedést elérni. Nézzük az egyik évben a GDP-t, a következőben a GDP-t, és vegyük a logaritmust, hogy megtaláljuk az implicit növekedési rátát.

a természetes logaritmus (Ln(x)) két kedvenc értelmezése, azaz a természetes naplója 1.5:

• 100% – os növekedést feltételezve, mennyi ideig kell növekednie, hogy elérje az 1,5-et? (.405, kevesebb, mint az időtartam fele)
• feltételezve, hogy 1 időegység, milyen gyorsan kell növekednie, hogy elérje az 1,5-et? (40.Évente 5%, folyamatosan kiegészítve)

a logaritmus az, amivel rájövünk, milyen gyorsan növekszünk.

mérési skála: Google PageRank

a Google az interneten minden oldalnak ad egy pontszámot (PageRank), amely a tekintély / fontosság durva mértéke. Ez egy logaritmikus skála, ami a fejemben azt jelenti, hogy “a PageRank megszámolja a pontszám számjegy számát”.

tehát egy pagerank 2 (“2 számjegy”) oldal 10x népszerűbb, mint egy PageRank 1 oldal. Az oldalam a PageRank 5, a CNN pedig a PageRank 9, tehát 4 nagyságrendű különbség van ($10^4$ = 10,000).

nagyjából elmondható, hogy körülbelül 7000 látogatást kapok naponta. Az én boríték matek, azt hiszem, CNN kap körülbelül 7000 * 10,000 = 70 millió látogatás / nap. (Hogy csináltam ezt? A fejemben azt hiszem, $7k * 10k = 70 * k * k = 70 * m$). Lehet, hogy egy párszor több, mint, hogy (100M, 200m), de valószínűleg nem akár 700M.

Google közvetít egy csomó információt egy nagyon durva skála (1-10).

mérési skála: Richter, Decibel stb.

sóhaj. A tipikus “logaritmusok a Való Világban” példánál vagyunk: Richter-skála és Decibel. Az ötlet az, hogy a drasztikusan változó eseményeket (földrengéseket) egyetlen skálán, kis tartományban (általában 1-10) helyezzük el. Csakúgy, mint a PageRank, minden 1 pontos növekedés 10-szeres teljesítményjavulást jelent. A legnagyobb ember által feljegyzett földrengés 9,5 volt; a Yucat-félsziget becsapódása, amely valószínűleg kihalt a dinoszauruszokat, 13 volt.

a decibelek hasonlóak, bár negatívak is lehetnek. A hangok az intenzíven csendestől (pindrop) a rendkívül hangosig (Repülőgép) terjedhetnek, és az agyunk mindent képes feldolgozni. A valóságban egy repülőgép motorjának hangja milliószor (milliárd, billió) erősebb, mint egy pindrop, és kényelmetlen, ha egy skála 1-től egy gazillionig terjed. A naplók mindent ésszerű skálán tartanak.

logaritmikus grafikonok

gyakran látni fogja a “log skálán”ábrázolt elemeket. A fejemben ez azt jelenti, hogy az egyik oldal a “számjegyek számát” vagy a “szorzások számát” számolja, nem magát az értéket. Ismét ez segít megmutatni vadul változó események egyetlen skálán (megy 1-10, nem 1 milliárd).

Moore törvénye nagyszerű példa: 18 havonta megduplázzuk a tranzisztorok számát (kép jóvoltából Wikipedia).

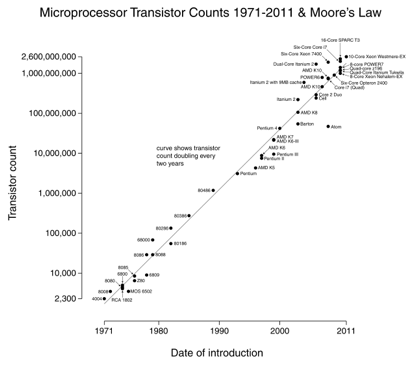
a log-skála grafikonokban az a szép, hogy az exponenciális változások (a processzor sebessége) egyenes vonalként jelennek meg. Az évi 10x-es növekedés azt jelenti, hogy folyamatosan felfelé halad a “számjegyek” skálán.

tovább és felfelé

ha egy fogalom jól ismert, de nem szeretett, ez azt jelenti, hogy építenünk kell az intuíciónkat. Keresse meg a működő analógiákat, és ne elégedjen meg azzal a moslékkal, amelyet egy tankönyv üget. A fejemben:

• a logaritmusok megtalálják a hatás kiváltó okát (lásd növekedés, kamatláb keresése)
• segítenek megszámolni a szorzásokat vagy számjegyeket, a részszámlálás bónuszával (500k egy 6,7 jegyű szám)

Boldog matekot.

Egyéb Hozzászólások ebben a sorozatban

1. egy intuitív útmutató exponenciális függvények & e
2. Demystifying természetes logaritmus (ln)
3. a vizuális útmutató az egyszerű, összetett és folyamatos kamatlábak
4. közös meghatározása e (színezett)
5. a kitevők megértése (miért 0^0 = 1?)
6. logaritmusok használata a Való Világban
7. hogyan gondolkodjunk Kitevőkkel és Logaritmusokkal
8. diszkrét vs. folyamatos növekedés megértése
9. mit jelent valójában egy kitevő?
10. K: Miért különleges az e? (2.718…, nem 2, 3,7 vagy más szám?)