hurtig G-kode Arc Tutorial: gør G02 & G03 let, undgå fejl

cirkulær Interpolation er bevægelse langs en cirkulær bue

når vi lige er færdig med at diskutere lineær interpolation eller bevægelse i en lige linje, kommer vi næste til cirkulær interpolation, som er bevægelse langs en cirkulær bue. Bortset fra den ret eksotiske evne til at følge en “NURBS”-sti understøtter de fleste G-kode-controllere kun to slags bevægelser: lineær og cirkulær. Cirkulær interpolation er ganske lidt mere krævende på din maskine, da to akser skal koordineres nøjagtigt. Tegning af en komplet cirkel involverer ikke kun koordineret bevægelse, men vending af retning ved hvert af de 4 kvadrantpunkter. Disse ville være de punkter, der svarer til 0, 90, 180 og 270 grader. Hvis maskinen overhovedet har nogen tilbageslag, vil det være tydeligt ved disse tilbageførsler, fordi der vil være en fejl i snittet der.

cirkulær bevægelse er en tilstand initieret via G02 og G03

ligesom lineær bevægelse (initieret af G00 og G01), cirkulær bevægelse er en tilstand initieret via G02 eller G03. G02 etablerer en tilstand for cirkulære buer med uret. G03 etablerer en tilstand til cirkulære buer mod uret.

definition af en bue til CNC-controlleren

når enten G02-eller G03-tilstanden er etableret, defineres buer i G-kode ved at identificere deres 2 endepunkter og det center, der skal være lige langt fra hvert endepunkt, ellers vil der opstå en alarm. Slutpunkterne er nemme. Det aktuelle kontrolpunkt eller placering, når blokken startes, etablerer et slutpunkt. Den anden kan etableres ved hjælp af koordinater. Centret er lidt mere komplekst.

definition af centrum via IJK Relative forskydninger

centret identificeres oftest ved hjælp af I, J eller K til at etablere relative forskydninger fra udgangspunktet for buen til midten. Her er en typisk lysbue med uret:

definition af en bue ‘ s center med IJK…

denne bue starter ved 0Y2 og slutter ved 2Y0. Det er centrum på 0Y0. Vi kunne specificere det i g-kode som denne:

G02 (Indstil lysbuetilstand med uret)

2Y0 I0J-2.0

I og J angiver relative koordinater fra startpunktet til midten. Med andre ord, hvis vi tilføjer i-værdien til startpunktets H, og J-værdien til startpunktets Y, får vi H og Y til midten.

definition af centrum Via Radius ved hjælp af “R”

vi kan også definere midten bare ved at specificere cirkelens radius. I dette tilfælde har vores cirkel en radius på 2, så g-koden kan simpelthen være:

G02

H2Y0 R2

mange af jer vil beslutte lige her og nu, da R er lettere at forstå og kortere at skrive, skal du bare bruge R og glemme IJK. Men CNC-lærerne i verden vil foreslå, at du foretrækker IJK. Deres argument er, at når du bruger IJK, får du en dobbeltkontrol, at din bue er korrekt.

hvorfor?

fordi controlleren får beregne et faktisk sæt koordinater for centret via IJK. Når det har centrets koordinater, kan det kontrollere, at det er lige langt fra begge slutpunkter. Kontrollen af hver af disse to afstande er dobbeltkontrol. I tilfælde af” R ” – formatet har controlleren ingen sådan dobbeltkontrol. Det skal vælge et center, der garanterer lige afstand.

personligt ved jeg ikke, om jeg er enig med CNC-instruktørerne, at dette giver nogen ekstra kontrol eller ej. Jeg siger, at gå med den tilgang, der giver mening for din særlige situation, men du skal bestemt være fortrolig og komfortabel med begge dele. Du bliver nødt til at være fortrolig med relative koordinater alligevel, da de er darned handy. Kan lige så godt blive komfortabel nu.

det er lidt som at få at vide, at du kun skal bruge 4-kæbe chuck på en drejebænk, når du først starter, så du får det meget behageligt at ringe det ind. Det er en god færdighed at være god til som maskinarbejder!

variationer i Arc syntaks for forskellige G-kode dialekter og tilstande

når IJK ikke er inkrementelle, og hvad med at have både IJK og R? Plus, andre modale Shenanigans og Arc variationer

dette er et andet af de steder, hvor mange uklare ting sker, og du skal vide, hvad din controller vil gøre uden at antage noget. Generelt skal reglen være, at hvis du har både IJK og R i samme blok, har R forrang, og IJK ignoreres. Men der er controllere, der ikke fungerer nøjagtigt på den måde, så vær sikker på at du ved, hvad der foregår.

G-guiden Editor lader dig angive flere parametre i sin Post, der bestemmer, hvordan buer arbejde. Her er et skærmbillede af opsætningsindstillingerne:

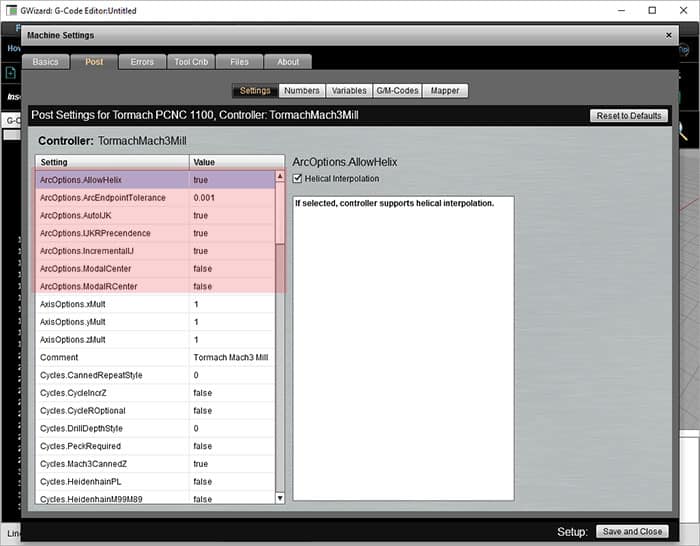
Arc muligheder for G-kode Simulering

lad os gå over disse muligheder:

– Inkremental vs absolut IJK: vi har diskuteret IJK som tilbyder koordinater i forhold til udgangspunktet for centret. Tilføj I til Y, J til Y og K til Å af udgangspunktet, så får du midten. Mange kontroller har også muligheden for, at IJK er centrets absolutte koordinater.

– modale IJK-Centre: når IJK er absolutte centerkoordinater, vil nogle controllere huske det sidst definerede center, hvorfor IJK er modal i så fald. Når du bruger en kontrolopsætning som denne, kan du bare fortsætte med at udstede kommandoer til buer uden at skulle definere et nyt center hver gang. Det er dog ikke klart–at du sparer meget-hvor ofte vil du lave en flok buer med det samme center?

– modale r-Centre: en anden variation på den modale centeridee er at tillade radius defineret af “R” at være modal. Uanset hvad den sidst anvendte r var, husker controlleren og bruger denne værdi igen, hvis der ikke gives R. Dette virker mere nyttigt end modal IJK. For eksempel kan en lomme have buer til hjørnerne, der alle har samme radius.

– Giv R forrang: som nævnt vil de fleste controllere bruge “R”, når både “R” og “IJK” gives i samme blok. Men denne mulighed giver dig mulighed for at ændre denne forrang til IJK, hvis din controller fungerer på den måde i stedet.

– Spiralformet Interp.: Denne indstilling regulerer, om din controller tillader spiralformet interpolation.

det mest almindelige Problem konfiguration af en CAM Post eller CNC Simulator: Absolut vs relativ IJK

vi har alle haft oplevelsen af at se på en backplot (eller værre, se det i selve værktøjsbevægelsen, som er ret skræmmende) og se de kæmpe næsten komplette cirkler og intet tegn på de velkendte delbevægelser, vi forventede at se. Her er et typisk eksempel:

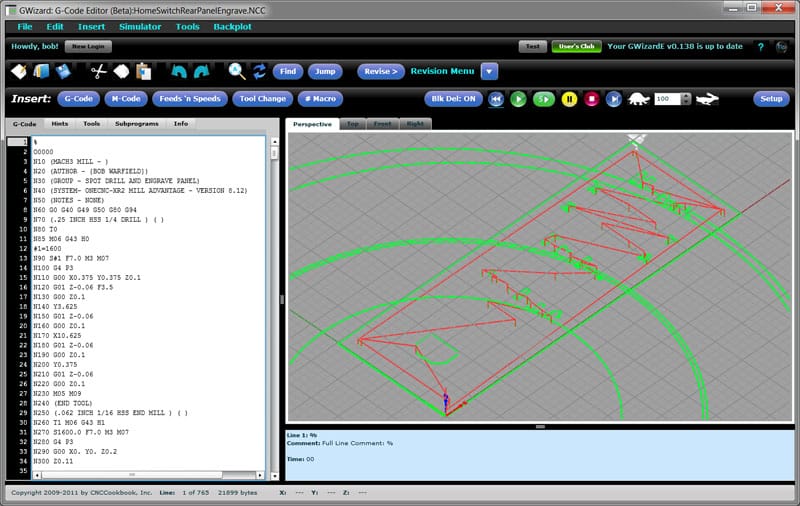
Indgraver fil med dårlige postindstillinger for buer…

hvis du ser den slags ting, er den første ting at kontrollere absolut versus relativ IJK for buer. Indstillingen skal matche mellem, hvad CAM producerer, og hvad controlleren eller simulatoren forventer.

prøv vores G-kode Simulator og Editor, gratis

fraktioner af en cirkel, kvadranter og controllere

det første ved en bue er, at det ikke er muligt at specificere mere end en 360 graders bue. Der er nogle undtagelser fra dette på nogle controllere til spiralformet Interpolation (se nedenfor), bare fordi det kan være nyttigt for spiraler. Når en fuld cirkel ønskes, skal du indstille start-og slutpunkterne lig med hinanden:

G01 H3. 25 Y2.0

G02 H3.25 Y2.0 I-1.25 J0

interessant nok kan du ikke angive en fuld cirkel med “R” notationen. Dette skyldes, at der er et uendeligt antal cirkler, der starter og slutter på samme punkt af en bestemt radius, så controlleren har ingen anelse om, hvad den korrekte cirkel kan være.

der er mere sjov forretning stadig med “R” og større buer. For eksempel kan en bue stadig have en bestemt radius og med uret (eller mod uret), men midten er tvetydig, hvis du rejser mere end 90 grader. For eksempel:

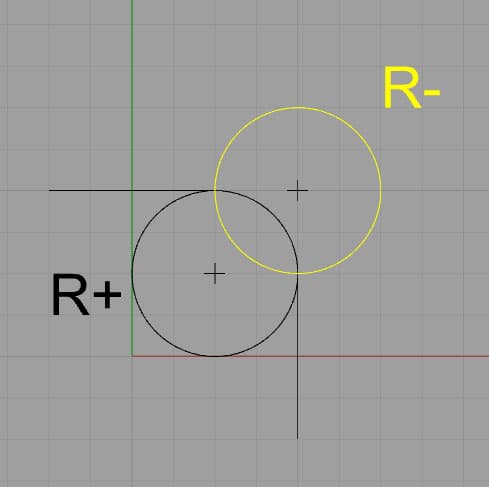
hvis R er negativ, tager den længere vej (i gul). Positiv får den kortere vej.

i betragtning af de to viste valg vælger controlleren stien baseret på radiustegnet. Negative kræfter jo længere bue, positiv jo kortere. Det negative tegn tvinger controlleren til at søge en levedygtig bue på mere end 180 grader.

nogle controllere er touchier stadig og vil ikke programmere en bue, der krydser en kvadrantlinje. Derfor er den største vinkel, en bue kan følge, 90 grader, og den vinkel må ikke krydse 0, 90, 180 eller 270 grader. For vinkler på 90 grader, der krydser en kvadrantlinie, skal de brydes i to stykker, hvor sammenføjningen mellem stykkerne er lige på kvadrantlinjen.

Fuldcirkler med ingen hastighed

Fuldcirkler opstår, når start-og slutpunkterne er identiske, og midten er specificeret via IJK (husk, r fører til et uendeligt antal cirkler). I betragtning af at du ønsker, at start-og slutpunktet skal være det samme, behøver du muligvis ikke at gider selv at specificere slutpunktet med . Nogle controllere kan kræve det, men de fleste gør det ikke. Her er et simpelt G-kode program, der producerer 3 cirkler på denne måde:

N45 G0 * 2. Y. 75
N46 G1 Å -.5 F10.
N47 Y. 5 F30. S2000
N48 G2 J-1, 1
N49 G1 Y, 75
N50 G, 2
N51 G0 H, 75 Y-3, 4
N52 G1 Å-.5 F10.
N53 * 5 F30.
N54 G2 I-1, 1
N55 * 75
N56 * 2
N57 G0 * 4, 75 Y-3, 4
N58 G1* -.5 F10.
N59-4, 5 F30.
N60 G2 I1. 1
N61 G1 * 4, 75
N62*. 2

og her er hvad backplot ser ud:

Tip til at gøre Arc programmering enklere: Start med segmenter

når jeg lægger en værktøjssti, foretrækker jeg at forlade buerne til sidst. I stedet for hver Bue sætter jeg simpelthen et linjesegment, hvis slutpunkter svarer til bueens slutpunkter. Dette gør det nemt at få den grove skitse af værktøjsstien sammen hurtigt, og det ser ofte ud til at gøre det lettere at derefter gå tilbage og konvertere linjerne til buer, når grundstrukturen allerede er på plads.

spiralformet Interpolation

en spiral er en bue, der kontinuerligt bevæger sig i en tredje dimension, som en skruegevind. Med spiralformet interpolation specificerer vi en sådan bue med G02/G03 for at bevæge kutteren langs en spiral. Dette kan gøres til gevindfræsning, interpolering af et hul eller en række andre formål. Her er en backplot fra et 1/4 “NPT trådmølleprogram:

spiral til gevindfræsning…

her er en prøve af koden fra gevindfræsningsprogrammet:

G01 G91 med – 0,6533 F100.
G01 G42 D08 * 0. 0235 Y-0, 0939 F10.
G03 * 0.0939 Y0.0939 -0.0179 R0.0939
G03 * 0, 1179 Y0.1179 -0.0179 R0.1179
G03 * 0, 1185 Y-0, 1185 -0.0179 R0.1185
G03 H0.1191 Y-0, 1191 H0.0179 R0.1191 F16.
G03h0. 1196h0.1196h0.0179h0.1196h960h03h0.1202h0.1202h0. 0179h0. 1202h26.
G03 * -0, 1207 Y-0, 1207 * 0.0179 R0.1207
G03 * 0.1213 Y-0, 1213 * 0.0179 R0.1213
G03 * 0.1218 Y0.1218 * 0.0179 R0.1218
G03 * -0.0975 Y0.0975 til 0.0179 R0.0975

dette er ” r ” (radius) format for buerne, og bemærk, at der er en å-koordinat for at specificere en dybdeændring for slutpunktet for hver bue. Denne kode bruger relativ bevægelse (G91), så hver “0,0179” bevæger skæret 0,0179″ dybere.

G-guiden Editor giver nogle virkelig nyttige oplysninger til at hjælpe med at forstå spiralformet interpolation. Her er hinten fra den tredje linje (første bue flytte):

Bemærk trådhøjden her beregnes som 0,1″

GVI måler og fortæller spiralhøjden, som i dette tilfælde er 0,100″. Det kan være nyttigt til at identificere, hvilken slags tråd der formales. Vi kan også se, at denne særlige bue løber fra 270 grader til en scosh mere end nul (0,1 grader).

vi gennemgår trådfræsning meget mere detaljeret i et senere kapitel, der udelukkende er afsat til emnet. For nu ville vi bare have dig til at være bekendt med ideen om, at du kan lave spiraler såvel som flade todimensionelle buer.

Making Toolpaths din maskine vil være lykkeligere med

når fræseren skifter retning, tilføjer den en vis mængde stress. Skæret vil bide i materialet enten mere eller mindre end det havde været, afhængigt af om retningerne ændrer sig mod emnet (eller uklippet materiale) eller væk fra det. Din maskine vil være meget gladere, hvis du programmerer en bue snarere end en pludselig retningsændring. Selv en bue med en meget lille radius gør det muligt for controlleren at undgå at ændre retning med det samme, hvilket i bedste fald kan efterlade et mærke i finishen og i værste fald forårsage snak eller andre problemer. For små retningsændringer er det måske ikke det værd. Men jo mere brat ændringen, med 90 grader er meget brat, jo større er sandsynligheden for, at du skal bruge en bue til at lette gennem svinget.

buer er også en nyttig måde at komme ind i snittet i stedet for at have skæreprammen lige ind. For information om indtastning af snittet med en bue, se værktøjsbanen side fra fræsning Feeds og hastigheder kursus.

øvelser

1. Grav din CNC controller manual ud, og gå gennem arc-indstillingerne for at konfigurere GVI, så de passer til din kontrols måde at fungere på.

2. Gør nogle etch-A-sketch eksperimenter med GVI. Opret nogle værktøjsbaner, der inkluderer buer, indtil du har det godt med at oprette dem.

Næste Artikel: Kører G-kode Simulator

prøv den gratis prøveversion af G-guiden G-kode Editor…