Bootstrap in R

Bootstrap è un metodo di inferenza su una popolazione che utilizza dati di esempio.Bradley Efron lo ha introdotto per la prima volta in questocarta nel 1979.Bootstrap si basa sul campionamento con sostituzione dai dati di esempio. Thistechnique può essere utilizzato per stimare l’errore standard di qualsiasi statistica e toobtain un intervallo di confidenza (CI) per esso. Bootstrap è particolarmente utile quando CI non ha una forma chiusa, o ne ha una molto complicata.

Supponiamo di avere un campione di n elementi:X = {x1, x2, …, xn} e siamo interessati a CI per qualche statistica T = t(X). Bootstrapframework è semplice. Ripetiamo solo R volte il seguente schema: Per la ripetizione i-esima, campione con elementi di sostituzione n dal campione disponibile (alcuni di essi verranno raccolti più di una volta). Chiama thisnew sample i-esimo bootstrap sample, Xi e calculatedesired statistic Ti = t (Xi).

Di conseguenza, otterremo i valori R della nostra statistica: T1, T2,…, TR. Li chiamiamo realizzazioni di bootstrap di T o una distribuzione di bootstrap di T. Sulla base di esso, possiamo calcolare CI per T. Ci sono diversi modi di farlo. Prendere percentili sembra essere il più facile.

Bootstrap in azione

Usiamo (ancora una volta) il noto set di dati iris. Dai un’occhiata a una prima riga:

Supponiamo di voler trovare CIs per mediana Sepal.Length, medianaSepal.Width e coefficiente di correlazione di rango di Spearman tra thesetwo. Useremo il pacchetto R boot e una funzione chiamata… boot. Touse la sua potenza dobbiamo creare una funzione che calcola ourstatistic (s) di dati ricampionati. Dovrebbe avere almeno twoarguments: un dataset e un vettore contenente indices di elementsfrom un set di dati che sono stati raccolti per creare un esempio di bootstrap.

Se vogliamo calcolare CIs per più di una statistica alla volta, ourfunction deve restituirli come un singolo vettore.

Per il nostro esempio, potrebbe assomigliare a questo:

library(boot)foo <- function(data, indices){ dt<-data c( cor(dt, dt, method='s'), median(dt), median(dt) )}

foo sceglie di elementi desiderati (che i numeri sono memorizzati in indices)da data e calcola il coefficiente di correlazione delle prime due colonne(method='s' è utilizzato per scegliere di rango di Spearman coefficientemethod='p' sarà il risultato con coefficiente di Pearson) e la loro mediane.

Possiamo anche aggiungere alcuni argomenti aggiuntivi, ad es. lascia che l’utente scelga il tipo odcorrelation coefficient:

foo <- function(data, indices, cor.type){ dt<-data c( cor(dt, dt, method=cor.type), median(dt), median(dt) )}

Per rendere questo tutorial più generale, userò l’ultima versione difoo.

Ora, possiamo usare la funzione boot. Dobbiamo fornirlo con un nome oddataset, funzione che abbiamo appena creato, numero di ripetizioni (R)e qualsiasi argomento aggiuntivo della nostra funzione (come cor.type). Di seguito, Iuse set.seed per la riproducibilità di questo esempio.

set.seed(12345)myBootstrap <- boot(iris, foo, R=1000, cor.type='s')

boot funzione restituisce un oggetto della classe chiamata… (sì, hai ragione!)boot. Ha due elementi interessanti. $t contiene i valori R dei ourstatistic generati dalla procedura bootstrap (bootstrap realizations ofT):

$t0 contiene i valori delle nostre statistiche in originale, completo, dataset:

myBootstrap$t0## -0.1667777 5.8000000 3.0000000

Stampa boot oggetto alla console fornisce alcune ulteriori informazioni:

original è lo stesso di $t0. bias è una differenza tra la media delle realizzazioni di bootstrap (quelle di $t), chiamata stima di bootstrap di T e valore nel set di dati originale (quello di $t0).

colMeans(myBootstrap$t)-myBootstrap$t0## 0.002546391 -0.013350000 0.007900000

std. error è un errore standard di stima bootstrap, che equivale alla deviazione standard delle realizzazioni bootstrap.

apply(myBootstrap$t,2,sd)## 0.07573983 0.10295571 0.02726414

Diversi tipi di bootstrap CIs

Prima di iniziare con CI, vale sempre la pena dare un’occhiata aldistribuzione delle realizzazioni bootstrap. Possiamo usare la funzione plot, conindex che indica a quale delle statistiche calcolate in foo vogliamo guardare. Qui index=1 è un coefficiente di correlazione di Spearman betweensepal length e width, index=2 è una lunghezza mediana del sepalo od e index=3 è una larghezza mediana del sepalo od.

plot(myBootstrap, index=1)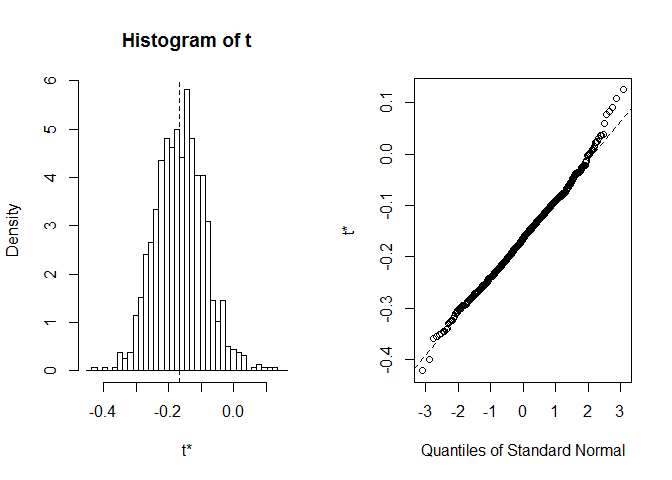

La distribuzione dei coefficienti di correlazione di bootstrap sembra quitenormal-like. Troviamo un informatore. Possiamo usare boot.ci. Il valore predefinito è CIS del 95%, ma può essere modificato con il parametro conf.

boot.ci fornisce 5 tipi di CIS bootstrap. Uno di loro, studentizedinterval, è unico. Ha bisogno di una stima della varianza bootstrap. Non lo forniamo, quindi R stampa un avviso:bootstrap variances needed for studentized intervals. Varianceestimates può essere ottenuto con bootstrap di secondo livello o (più facile) withjackknife technique. Questo è in qualche modo oltre lo scopo di questo tutorial,quindi concentriamoci sui restanti quattro tipi di CIS bootstrap.

Se non vogliamo vederli tutti, possiamo scegliere quelli rilevanti nell’argomento type. I valori possibili sono norm, basic, stud, perc, bca ora vettore di questi.

La funzione boot.ci crea oggetto di classe… (sì, hai indovinato!)bootci. I suoi elementi sono chiamati proprio come i tipi di CI utilizzati nell’argomento type. $norm è un vettore a 3 elementi che contiene livelli di confidenza e limiti CI.

boot.ci(myBootstrap, index=1, type='norm')$norm## conf ## 0.95 -0.3177714 -0.02087672

$basic, $stud, $perc e $bca sono vettori a 5 elementi che contengono anche percentili usati per calcolare CI (torneremo su questo più tardi):

boot.ci(myBootstrap, index=1, type='basic')$basic## conf ## 0.95 975.98 25.03 -0.3211981 -0.03285178

Un po ‘ di notazione (Mi dispiace!)

Per avere un’idea di quali sono i diversi tipi di CI, dobbiamo introdurrealcune notazioni. Quindi, lascia:

• t⋆ essere il bootstrap stima (media di bootstraprealizations),
• t0 essere un valore della statistica del set originale,
• se⋆ essere un errore standard della stima bootstrap,
• b essere un bias di bootstrap estimateb = t⋆ − t0
• α essere un livello di confidenza, in genere α = 0.95,
• za essere un $1-\frac \alpha 2$-quantile di standardnormal distribuzione,
• sarebbe essere un α-percentile della distribuzione di bootstraprealizations.

CI percentile

Con la notazione precedente, CI percentile è:

(θ (1-α) / 2, θ1- (1-α)/2)

quindi questo richiede solo percentili rilevanti. Niente di più.

CI normale

Un CI tipico di Wald sarebbe:

t0 ± za se se⋆

ma nel caso di bootstrap, dovremmo correggerlo per pregiudizi. Quindi diventa:

t t_0 – b \pm z_\alpha \cdot se^\star \\2t_0 – t^\star \pm z_\alpha \cdot se^\star

Basic CI

Percentile CI non è generalmente raccomandato perché si comporta in modo scadente quando si tratta di distribuzioni dalla coda strana. L’IC di base (chiamato anche icpivotale o empirico) è molto più robusto a questo. Il rationalebehind è quello di calcolare le differenze tra ogni replica bootstrap e t0 e utilizzare i percentili della loro distribuzione. I dettagli completi possono essere trovati, ad esempio in All ofStatistics di L. Wasserman

La formula finale per l’IC di base è:

(2t0 − θ1 − (1 − α)/2, 2t0 − θ (1-α)/2)

BCa CI

BCa viene da bias corretto, accelerato. La formulaper non è molto complicata ma un po ‘ poco intuitiva, quindi lo salterò.Vedi l’articolo di Thomas J. DiCiccio e BradleyEfron se sei interessato ai dettagli.

L’accelerazione menzionata nel nome del metodo richiede l’utilizzo di specificpercentiles di realizzazioni bootstrap. A volte può accadere thatthese sarebbe alcuni percentili estremi, possibilmente valori anomali.BCa può essere instabile in questi casi.

Diamo un’occhiata a BCa CI per la mediana della larghezza del petalo. Nel set di dati originale, questa mediana equivale precisamente a 3.

Otteniamo BCa CI (2.9, 2.9). È strano, ma per fortuna R ci ha avvertito che extreme order statistics used as endpoints. Vediamo cosa è successo esattamente qui:

plot(myBootstrap, index=3)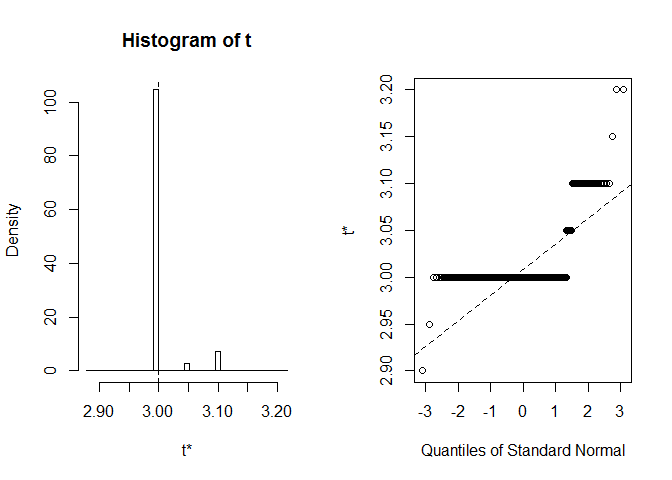

La distribuzione delle realizzazioni bootstrap è insolita. Una stragrande maggioranza ofthem (oltre il 90%) sono 3s.

table(myBootstrap$t)#### 2.9 2.95 3 3.05 3.1 3.15 3.2## 1 1 908 24 63 1 2

Replica dei risultati

A volte, è necessario ricreare le repliche di bootstrap. Se possiamo usare R per questo, questo non è un problema. set.seed funzione risolve il problema.Ricreare le repliche di bootstrap in altri software sarebbe molto più complicato. Inoltre, per la grande R, il ricalcolo in R può anche essere un’opzione (per mancanza di tempo, ad esempio).

Possiamo affrontare questo problema, salvando indici di elementi dell’originaldataset, che formavano ogni campione di bootstrap. Questo è ciò che fa la funzione boot.array(con l’argomento indices=T).

tableOfIndices<-boot.array(myBootstrap, indices=T)

Ogni riga è un esempio di bootstrap. Ad Es., il nostro primo esempio contiene gli elementi seguenti:

Impostazione indices=F (un default), otterremo una risposta alla domanda “Howmany volte ogni elemento del set di dati originale è apparso in ogni bootstrapsample?”. Ad esempio, nel primo campione: è apparso il 1 ° elemento del dataset, il 2 ° elemento non è apparso affatto, il 3 ° elemento è apparso una volta, il 4 ° due e così via.

Una tabella come questa ci consente di ricreare la realizzazione di bootstrap all’esterno di R.O in R stesso quando non vogliamo usare set.seed e fare di nuovo tutto il calcolo.

onceAgain<-apply(tableOfIndices, 1, foo, data=iris, cor.type='s')

Controlliamo se i risultati sono gli stessi:

Sì, lo sono!

Se vuoi saperne di più sull’apprendimento automatico in R, segui il corso Toolbox di Machine Learning di DataCamp.