Differenza tra i filtri IIR e FIR: a practical design guide

Un filtro digitale è un algoritmo matematico che opera su un set di dati digitali (ad esempio i dati dei sensori) per estrarre le informazioni di interesse e rimuovere qualsiasi informazione indesiderata. Le applicazioni di questo tipo di tecnologia includono la rimozione di difetti dai dati del sensore o persino la pulizia del rumore su un segnale misurato per un’analisi dei dati più semplice. Ma come scegliere il miglior tipo di filtro digitale per la nostra applicazione? E quali sono le differenze tra un filtro IIR e un filtro FIR?

I filtri digitali sono suddivisi nelle seguenti due categorie:

• Risposta all’impulso infinita (IIR)
• Risposta all’impulso finita (FIR)

Come suggeriscono i nomi, ogni tipo di filtro è classificato in base alla lunghezza della sua risposta all’impulso. Tuttavia, prima di iniziare con un’analisi matematica dettagliata, è prudente apprezzare le differenze di prestazioni e caratteristiche di ciascun tipo di filtro.

Esempio

Al fine di illustrare le differenze tra un IIR e FIR, la risposta in frequenza di un FIR 14 ° ordine (linea continua), e un 4 ° ordine Chebyshev Tipo I IIR (linea tratteggiata) è mostrato di seguito in Figura 1. Si noti che sebbene gli spettri di magnitudine abbiano un grado di attenuazione simile, lo spettro di fase del filtro IIR è non lineare nella banda passante (\(\small 0 \ rightarrow7. 5Hz\)) e diventa molto non lineare alla frequenza di cut-off, \(\small f_c=7.5 Hz\). Si noti inoltre che l’FIR richiede un numero maggiore di coefficienti (15 vs 10 dell’IIR) per abbinare le caratteristiche di attenuazione dell’IIR.

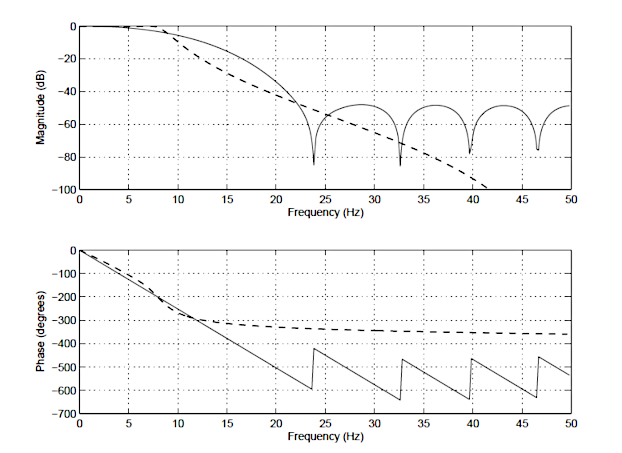
Queste sono solo alcune delle differenze tra i due tipi di filtri. Seguirà un riepilogo dettagliato dei principali vantaggi e svantaggi di ciascun tipo di filtro.

Filtri IIR

I filtri IIR (infinite impulse response) sono generalmente scelti per applicazioni in cui la fase lineare non è troppo importante e la memoria è limitata. Sono stati ampiamente utilizzati nell’equalizzazione audio, nell’elaborazione del segnale dei sensori biomedici, nei sensori intelligenti IoT/IIoT e nelle applicazioni di telecomunicazione/RF ad alta velocità.

Vantaggi

• Basso costo di implementazione: richiede meno coefficienti e memoria rispetto filtri FIR al fine di soddisfare un simile insieme di specifiche, cioè, frequenza di cut-off e attenuazione stopband.
• Bassa latenza: adatto per il controllo in tempo reale e molto ad alta velocità RF applicazioni in virtù del basso numero di coefficienti.
• Equivalente analogico: può essere usato per imitare le caratteristiche dei filtri analogici usando s – z plane mapping transforms.

Svantaggi

• Caratteristiche di fase non lineare: Le caratteristiche di fase di un filtro IIR sono generalmente non lineari, specialmente in prossimità delle frequenze di cut-off. I filtri di equalizzazione all-pass possono essere utilizzati per migliorare le caratteristiche di fase della banda passante.
• Analisi più dettagliata: richiede più scaling e analisi di overflow numerico quando implementato in punto fisso. La struttura del filtro Direct form II è particolarmente sensibile agli effetti della quantizzazione e richiede particolare attenzione durante la fase di progettazione.
• Stabilità numerica: Meno numericamente stabile rispetto alle loro controparti FIR (finite impulse response), a causa dei percorsi di feedback.

Filtri FIR

I filtri FIR (finite impulse response) sono generalmente scelti per applicazioni in cui la fase lineare è importante e sono disponibili una discreta quantità di memoria e prestazioni computazionali. Hanno un ampiamente distribuito in audio e applicazioni di miglioramento del segnale biomedico. La loro struttura all-zero (discussa di seguito) assicura che non diventino mai instabili per qualsiasi tipo di segnale di ingresso, il che conferisce loro un netto vantaggio rispetto all’IIR.

Vantaggi

• Fase lineare: gli ABETI possono essere facilmente progettati per avere una fase lineare. Ciò significa che nessuna distorsione di fase viene introdotta nel segnale da filtrare, poiché tutte le frequenze vengono spostate nel tempo della stessa quantità, mantenendo così le loro relazioni armoniche relative (cioè gruppo costante e ritardo di fase). Questo non è certamente il caso dei filtri IIR, che hanno una caratteristica di fase non lineare.
• Stabilità: poiché i FIR non utilizzano valori di output precedenti per calcolare il loro output attuale, ad es. non hanno feedback, non possono mai diventare instabili per qualsiasi tipo di segnale di ingresso, il che dà loro un netto vantaggio rispetto ai filtri IIR.
• Risposta in frequenza arbitraria: La funzione firarb() di Parks-McClellan e ASN FilterScript consente di progettare un FIR con una risposta di grandezza arbitraria. Ciò significa che un ABETE può essere personalizzato più facilmente di un IIR.
• Prestazioni a punto fisso: gli effetti della quantizzazione sono meno gravi di quelli di una IIR.

Svantaggi

• Elevato requisito computazionale e di memoria: Gli ABETI di solito richiedono molti più coefficienti per ottenere un taglio netto rispetto alle loro controparti IIR. La conseguenza di ciò è che richiedono molta più memoria e una quantità significativamente maggiore di operazioni MAC (multiple e accumulate). Tuttavia, le moderne architetture di microcontrollori basate sui core Cortex-M di Arm ora includono il supporto hardware DSP tramite SIMD (signal instruction, multiple data) che accelera significativamente l’operazione di filtraggio.
• Maggiore latenza: il maggior numero di coefficienti, significa che in generale un FIR è meno adatto di un IIR per applicazioni veloci ad alta produttività. Ciò diventa problematico per le applicazioni di controllo a circuito chiuso in tempo reale, in cui un filtro FIR potrebbe avere un ritardo di gruppo eccessivo per ottenere la stabilità del ciclo.
• Nessun equivalente analogico: utilizzando il bilineare, abbinato z-transform (s-z mapping), un filtro analogico può essere facilmente essere trasformato in un filtro IIR equivalente. Tuttavia, questo non è possibile per un FIR in quanto non ha equivalenti analogici.

definizioni Matematiche

Come discusso nell’introduzione, il nome IIR e FIR hanno origine dalle definizioni matematiche di ogni tipo di filtro, cioè un filtro IIR è classificato per la sua teoricamente infinite impulse response,

\(\displaystyle
y(n)=\sum_{k=0}^{\infty}h(k)x(n-k)
\)

e un ABETE classificati dal suo finite impulse response,

vediamo ora di analizzare le proprietà matematiche di ogni tipo di filtro, a sua volta.

Definizione IIR

Come visto sopra, un filtro IIR è classificato dalla sua risposta all’impulso teoricamente infinita,

\(\displaystyle y (n)=\sum_{k=0}^{\infty}h(k) x(n-k)\)

In pratica, non è possibile calcolare l’output di un IIR usando questa equazione. Pertanto, l’equazione può essere riscritta in termini di un numero finito di poli \(\piccolo p\) e zeri \(\piccolo q\), come definito dall’equazione della differenza di coefficiente costante lineare data da:

\(\displaystyle
y(n)=\sum_{k=0}^{q}b_k x(n-k)-\sum_{k=1}^{p}a_ky(n-k)
\)

dove \(\small a_k\) e \(\small b_k\) sono il filtro del denominatore e numeratore i coefficienti del polinomio, che affonda le sue radici pari al filtro poli e zeri, rispettivamente. Così, una relazione tra la differenza di equazione e la z-trasformata (funzione di trasferimento) può quindi essere definita tramite la z-trasformata ritardo di proprietà in modo tale che,

\(\displaystyle
\sum_{k=0}^{q}b_kx(n-k)-\sum_{k=1}^{p}a_ky(n-k)\quad\stackrel{\displaystyle\mathcal{Z}}{\longleftrightarrow}\quad\frac{\sum\limits_{k=0}^q b_kz^{-k}}{1+\sum\limits_{k=1}^p a_kz^{-k}}
\)

Come si è visto, la funzione di trasferimento è una rappresentazione nel dominio della frequenza del filtro. Si noti inoltre che i poli agiscono sui dati di output e gli zeri sui dati di input. Poiché i poli agiscono sui dati di uscita e influenzano la stabilità, è essenziale che i loro raggi rimangano all’interno del cerchio unitario (cioè <1) per la stabilità BIBO (bounded input, bounded output). I raggi degli zeri sono meno critici, in quanto non influenzano la stabilità del filtro. Questo è il motivo principale per cui i filtri FIR (risposta agli impulsi finita) all-zero sono sempre stabili.

stabilità BIBO

lineare tempo invariante (LTI) sistema (ad esempio un filtro digitale) è delimitata ingresso, delimitato uscita stabile, o BIBO stabile, se ogni delimitata ingresso dà luogo ad una delimitata uscita, come

\(\displaystyle \sum_{k=0}^{\infty}\left|h(k)\right|<\infty \)

Dove \(\small h(k)\) è la LTI del sistema di risposta all’impulso. Analizzando questa equazione, dovrebbe essere chiaro che il criterio di stabilità BIBO sarà soddisfatto solo se i poli del sistema si trovano all’interno del cerchio unitario, poiché la ROC (regione di convergenza) del sistema deve includere il cerchio unitario. Di conseguenza, è sufficiente dire che un segnale di ingresso limitato produrrà sempre un segnale di uscita limitato se tutti i poli si trovano all’interno del cerchio unitario.

Gli zeri d’altra parte, non sono vincolati da questo requisito, e di conseguenza possono trovarsi ovunque sul piano z, poiché non influenzano direttamente la stabilità del sistema. Pertanto, un’analisi della stabilità del sistema può essere effettuata calcolando in primo luogo le radici della funzione di trasferimento (cioè le radici dei polinomi numeratore e denominatore) e quindi tracciando i corrispondenti poli e zeri sul piano z.

Una situazione interessante si verifica se alcuni poli si trovano sul cerchio unitario, poiché il sistema si dice che sia marginalmente stabile, in quanto non è né stabile né instabile. Sebbene i sistemi marginalmente stabili non siano stabili BIBO, sono stati sfruttati dai progettisti di oscillatori digitali, poiché la loro risposta all’impulso fornisce un metodo semplice per generare onde sinusoidali, che si sono rivelate inestimabili nel campo delle telecomunicazioni.

Biquad IIR filters

L’implementazione del filtro IIR qui discussa è detta biquad, poiché ha due poli e due zeri come illustrato di seguito nella Figura 2. L’implementazione di biquad è particolarmente utile per implementazioni a punto fisso, poiché gli effetti della quantizzazione e della stabilità numerica sono ridotti al minimo. Tuttavia, il successo complessivo di qualsiasi implementazione di biquad dipende dalla precisione del numero disponibile, che deve essere sufficiente per garantire che i poli quantizzati siano sempre all’interno del cerchio unitario.

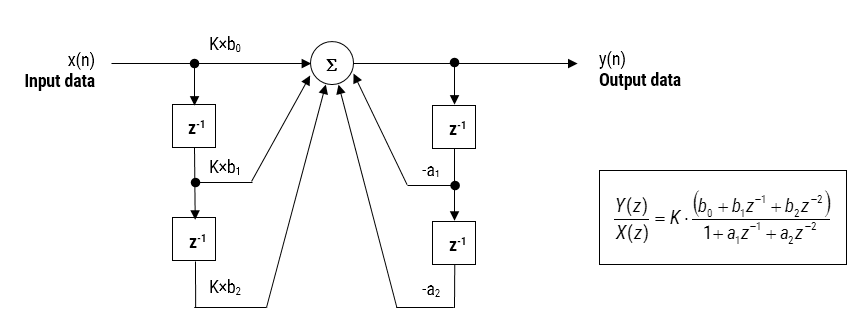
Figura 2: Forma diretta I (biquad) Realizzazione filtro IIR e funzione di trasferimento.

Analizzando la Figura 2, si può vedere che la struttura di biquad è in realtà composta da due percorsi di feedback (scalati da \(\small a_1\) e \(\small a_2\)), tre percorsi di avanzamento (scalati da \(\small b_0, b_1\) e \(\small b_2\)) e un guadagno di sezione, \(\small K\). Pertanto, l’operazione di filtraggio della Figura 1 può essere riassunta dalla seguente semplice equazione ricorsiva:

\(\displaystyle y (n)=K \ volte \ Grande-a_1 y (n-1) – a_2 y (n-2)\)

Analizzando l’equazione, si noti che l’implementazione di biquad richiede solo quattro aggiunte (che richiedono un solo accumulatore) e cinque moltiplicazioni, che possono essere facilmente ospitate su qualsiasi microcontrollore Cortex-M. Il guadagno di sezione, \(\small K\) può anche essere pre-moltiplicato con i coefficienti del percorso in avanti prima dell’implementazione.

Una collezione di filtri Biquad è indicata come una cascata Biquad, come illustrato di seguito.

ASN Filter Designer è in grado di progettare e implementare una cascata di fino a 50 biquad (solo Professional edition).

Implementazione in virgola mobile

Quando si implementa un filtro in virgola mobile (cioè utilizzando l’aritmetica a doppia o singola precisione) Le strutture di forma II diretta sono considerate una scelta migliore rispetto alla struttura di Forma I diretta. La struttura trasposta in forma diretta II è considerata la più accurata numericamente per l’implementazione in virgola mobile, poiché gli effetti indesiderati della sommersione numerica sono ridotti al minimo come si vede analizzando le equazioni di differenza.

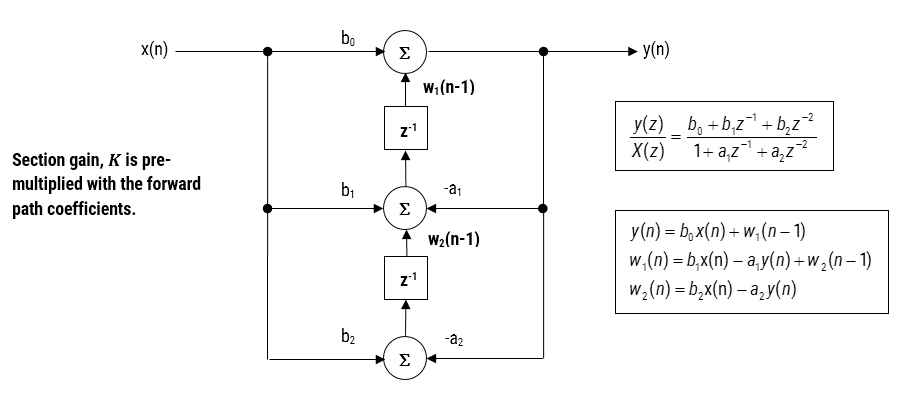
Figura 3-Direct Form II Transposed strucutre, transfer function and difference equations

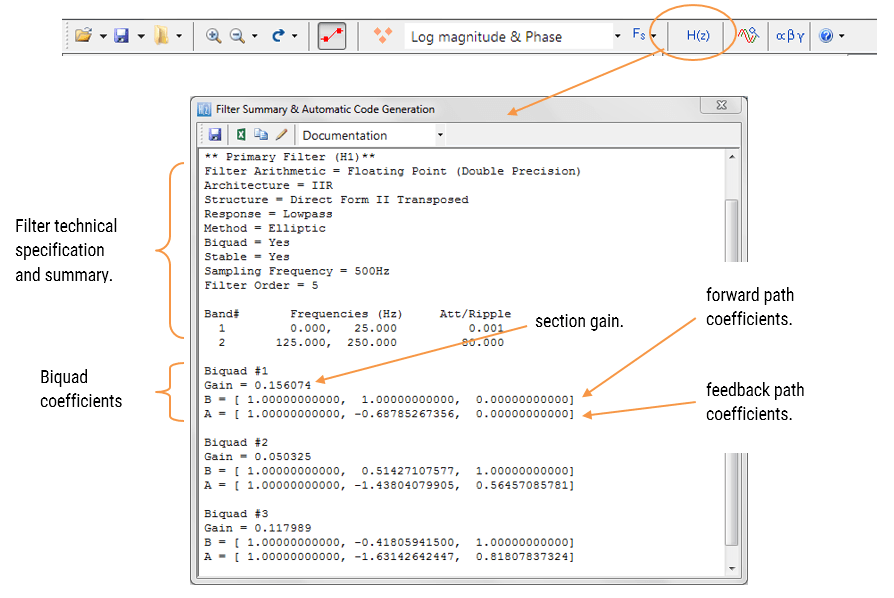
Il riepilogo del filtro (mostrato in Figura 4) fornisce al progettista una panoramica dettagliata del filtro progettato, incluso un riepilogo dettagliato delle specifiche tecniche e dei coefficienti del filtro, che presenta un percorso rapido e semplice per documentare il tuo progetto.

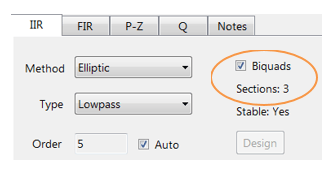
ASN Filter Designer supporta la progettazione e l’implementazione di filtri IIR a sezione singola e Biquad (impostazione predefinita).

Figura 4: specifiche dettagliate.

ABETE definizione

Restituzione del IIR lineare costante il coefficiente equazione alle differenze, cioè

\(\displaystyle
y(n)=\sum_{k=0}^{q}b_kx(n-k)-\sum_{k=1}^{p}a_ky(n-k)
\)

Si noti che, quando abbiamo impostato il \(\small a_k\) coefficienti (cioè il feedback a zero, la definizione riduce il nostro originale, il filtro FIR definizione, nel senso che la FIR di calcolo è basato sul passato e il presente di input di valori, vale a dire:

\(\displaystyle
y(n)=\sum_{k=0}^{q}b_kx(n-k)
\)

Implementazione

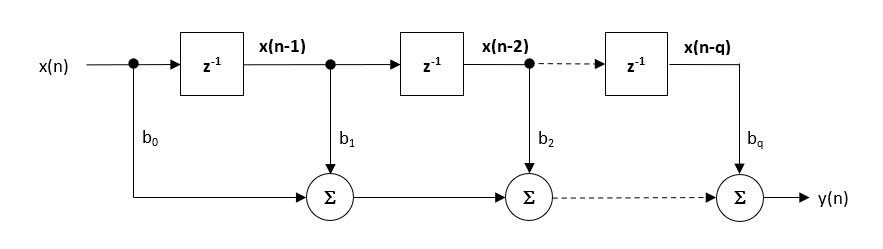
Sebbene esistano diverse implementazioni pratiche per FIR, la struttura della forma diretta e il suo cugino trasposto sono forse i più comunemente usati, e come tali, tutti i coefficienti di filtro progettati sono destinati all’implementazione in una struttura di forma diretta.

La struttura della forma diretta e l’equazione delle differenze associate sono mostrate di seguito. La Forma diretta è sostenuta per l’implementazione del punto fisso in virtù del concetto di accumulatore singolo.

\(\stile di visualizzazione y(n) = b_0x(n) + b_1x (n-1) + b_2x(n-2)+…. + b_qx(n-q) \)

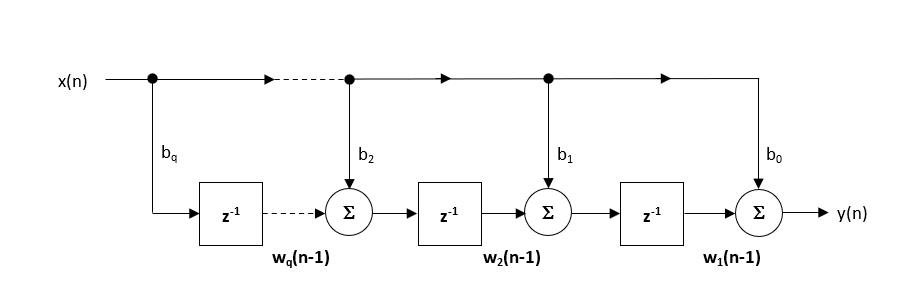
La struttura consigliata (predefinita) all’interno di ASN Filter Designer è la struttura trasposta in forma diretta, in quanto offre una precisione numerica superiore quando si utilizza l’aritmetica in virgola mobile. Ciò può essere facilmente visto analizzando le equazioni di differenza di seguito (utilizzate per l’implementazione), poiché gli effetti indesiderati della sommersione numerica sono ridotti al minimo, poiché l’aggiunta in virgola mobile viene eseguita su numeri di grandezza simile.

\(\displaystyle \begin{eqnarray}y(n) & = &b_0x(n) &+& w_1(n-1) \\ w_1(n)&=&b_1x(n) &+& w_2(n-1) \\ w_2(n)&=&b_2x(n) &+& w_3(n-1) \\ \vdots\quad &=& \quad\vdots &+&\quad\vdots \\ w_q(n)&=&b_qx(n) \end{eqnarray}\)

che Cosa abbiamo imparato?

I filtri digitali sono suddivisi nelle seguenti due categorie:

• Infinite impulse response (IIR)
• Finite impulse response (FIR)

I filtri IIR (infinite impulse response) sono generalmente scelti per applicazioni in cui la fase lineare non è troppo importante e la memoria è limitata. Sono stati ampiamente utilizzati nell’equalizzazione audio, nell’elaborazione del segnale dei sensori biomedici, nei sensori intelligenti IoT/IIoT e nelle applicazioni di telecomunicazione/RF ad alta velocità.

I filtri FIR (finite impulse response) sono generalmente scelti per applicazioni in cui la fase lineare è importante e sono disponibili una discreta quantità di memoria e prestazioni computazionali. Hanno un ampiamente distribuito in audio e applicazioni di miglioramento del segnale biomedico.

ASN Filter Designer fornisce agli ingegneri tutto ciò di cui hanno bisogno per progettare, sperimentare e implementare complessi filtri digitali IIR e FIR per una varietà di applicazioni di misurazione dei sensori. Questi vantaggi associati alla documentazione automatica e alla funzionalità di generazione del codice consentono agli ingegneri di progettare e convalidare un filtro digitale IIR/FIR in pochi minuti anziché in ore.