Fondamenti di Epidemiologia
Dopo la lettura di questo capitolo, si sarà in grado di effettuare le seguenti operazioni:
- Spiegare qual è l’effetto di una modifica
- Distinguere tra fattori confondenti e modificatori di effetto
- Condotta un’analisi stratificata per determinare se modificazione di effetto è presente nei dati
Nel precedente capitolo, abbiamo discusso di confondimento. Un confonditore, ricorderete, è una terza variabile che, se non controllata in modo appropriato, porta a una stima parziale dell’associazione. La modifica dell’effetto comporta anche una terza variabile (non l’esposizione e non il risultato)—ma in questo caso, non vogliamo assolutamente controllarlo. Piuttosto, la presenza di modificazione dell’effetto è di per sé una scoperta interessante, e la evidenziamo.
Quando è presente la modifica dell’effetto (chiamata anche interazione), ci saranno risultati diversi per diversi livelli della terza variabile (chiamata anche covariabile). Per esempio, se facciamo uno studio di coorte sulla quantità di sonno e GPA tra Oregon State University (OSU), gli studenti, nel corso di un periodo potremmo raccogliere questi dati:
| GPA | |||
| < 3.0 | ≥ 3.0 | ||
| Quantità di Sonno | < 8 ore | 25 | 25 |
| > 8 ore | 25 | 25 | |
Dal momento che questo è stato uno studio di coorte, si calcola il rapporto di rischio (RR):
Non esiste alcuna associazione tra la quantità di sonno e la successiva GPA. Utilizzando la frase modello, questo può essere affermato:
Questo è un rapporto di rischio da uno studio di coorte, quindi dobbiamo includere il lasso di tempo—che ho fatto dicendo “per terminare il termine”. Proprio come per confondere, ci riferiamo a questo come il RR non regolato o grezzo.
Tuttavia, parlando con gli studenti, ci chiediamo se il genere possa essere o meno un importante covariabile. Come nel caso di confusione, condurremo un’analisi stratificata per verificare la modifica dell’effetto. Ancora una volta, disegniamo tabelle 2 × 2 con la stessa esposizione (sonno) e risultato (GPA) ma disegniamo tabelle separate per uomini e donne (il genere è covariabile). Lo facciamo guardando indietro ai dati grezzi e capendo quante delle 25 persone nella cella A (E+, D+) sopra erano uomini e quante erano donne. Supponiamo che delle 25 persone che hanno riportato < 8 ore e hanno avuto un GPA < 3.0, 11 erano uomini e 14 erano donne. Quindi dividiamo allo stesso modo i partecipanti dalle celle B, C e D e creiamo tabelle 2 x 2 specifiche dello strato:
| Uomini | AAP | ||
| < 3.0 | ≥ 3.0 | ||
| Quantità di Sonno | < 8 ore | 11 | 14 |
| 8+ ore | 17 | 9 | |
| le Donne | GPA | ||
| < 3.0 | ≥ 3.0 | ||
| Quantità di Sonno | < 8 ore | 14 | 11 |
| 8+ ore | 8 | 16 | |
RRmen= \frac{(\frac{11}{25})}{(\frac{17}{26})} = 0.68
RRwomen= \frac{(\frac{14}{25})}{(\frac{8}{24})} = 1.7
Interpretazioni:
Tra gli studenti maschi, quelli che dormivano meno di 8 ore per notte avevano 0.68 volte il rischio di avere un GPA <3.0 alla fine del termine, rispetto a quelli che hanno riportato 8 o più ore.
Tra le studentesse, quelle che dormivano meno di 8 ore a notte avevano 1,7 volte il rischio di avere un GPA < 3,0 alla fine del termine, rispetto a quelle che hanno riportato 8 o più ore.
Dormire meno di 8 ore è associato—in questi dati ipotetici-a un GPA più alto tra gli studenti maschi (il “risultato” è un GPA basso, quindi un RR inferiore a 1 indica che gli individui esposti hanno meno probabilità di avere un GPA basso) ma con un GPA più basso tra le studentesse.
Il genere in questo caso agisce come modificatore di effetto: l’associazione tra sonno e GPA varia in base agli strati del covariabile. È possibile individuare la modifica dell’effetto quando si esegue l’analisi stratificata nel modo seguente:
- Le misure specifiche dello strato di associazione sono diverse tra loro
- Il greggio cade tra di loro
Se si dispone di modifica degli effetti, il passo successivo è quello di segnalare le misure specifiche dello strato. Non calcoliamo una misura aggiustata (sarebbe vicino a 1.0, simile al greggio); la cosa interessante qui è che uomini e donne reagiscono al sonno in modo diverso. La modifica degli effetti è qualcosa che vogliamo evidenziare nei nostri risultati, non qualcosa da regolare.
A differenza di confounding, dove una variazione del 10% da grezzo a rettificato è una definizione accettata per confondere, non esiste una tale definizione standardizzata per quanto diverse debbano essere le misure specifiche dello strato per chiamare qualcosa un modificatore di effetto. La soglia dovrebbe probabilmente essere superiore a quella necessaria per dichiarare qualcosa di confuso, perché una volta dichiarato qualcosa di un modificatore di effetto, sei successivamente obbligato a riportare i risultati separatamente per ogni livello del covariabile—qualcosa che riduce il tuo potere in almeno la metà. Pertanto, in epidemiologia, raramente vediamo prove di modificazione degli effetti riportate in letteratura. Per farla breve,” diverso “abbastanza per la modifica degli effetti è” inequivocabilmente diverso.”
Durante la lettura di articoli, la modifica degli effetti a volte viene chiamata interazione, o gli autori potrebbero semplicemente dire che stanno riportando analisi stratificate. Ognuna di queste 3 frasi è un indizio che c’è una variabile che agisce come un modificatore di effetto.
Effetto modifica Esempio II
A seguito della bolla immobiliare-driven recessione del 2008 (questa è l’esposizione), l’economia degli Stati Uniti ha perso un sacco di posti di lavoro. Ecco un grafico che mostra il numero di persone che lavoravano (il risultato) prima, durante e dopo la recessione. I risultati vengono presentati stratificati per genere (un covariabile), il che significa che l’analista sospettava che il genere potesse agire come modificatore di effetti. In effetti, i risultati sono leggermente diversi: gli uomini (in blu) hanno perso una percentuale maggiore di posti di lavoro e al 2014 non si erano ancora ripresi ai livelli pre-recessione, mentre le donne (in rosso) hanno perso meno posti di lavoro e nel 2014 si erano completamente ripresi.

Fonte: https://fred.stlouisfed.org/graph/fredgraph.png?g=qUs
E se ci stratificassimo anche per età? Primo, ecco un grafico che mostra come la recessione ha colpito posti di lavoro per le persone di età 55 e più anziani:
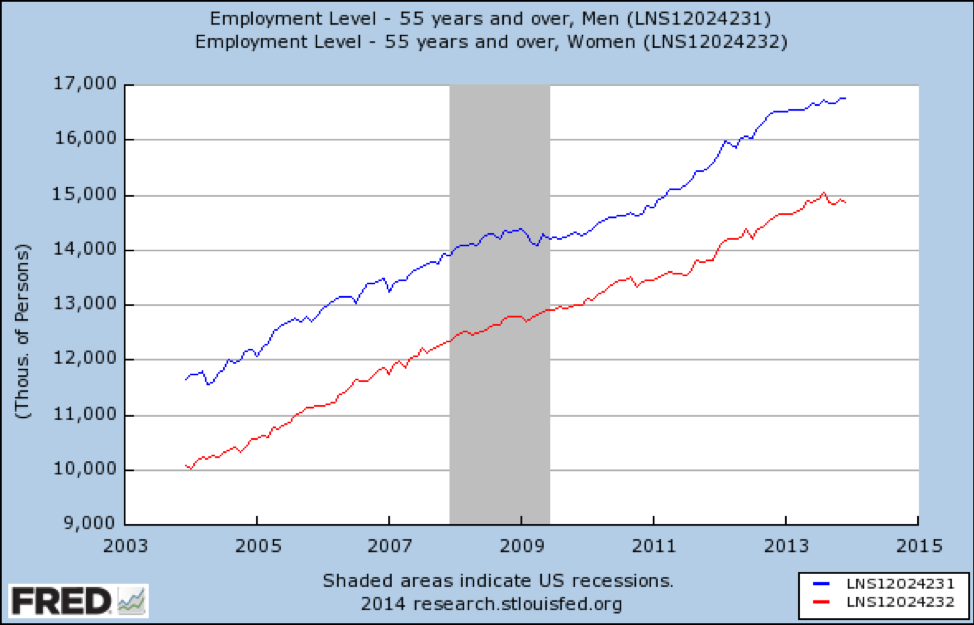
Fonte: https://fred.stlouisfed.org/graph/fredgraph.png?g=qUt
La recessione non ha influenzato gli americani che lavorano più anziani a tutti. Né stiamo vedendo la modifica dell’effetto per genere – le 2 linee sono quasi parallele.
Che dire dei giovani adulti?
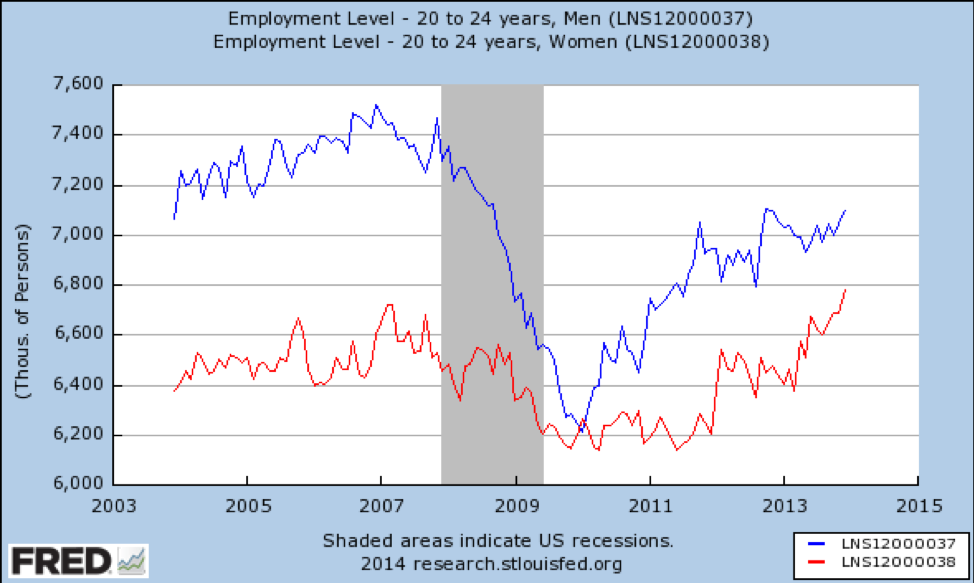
Fonte: https://fred.stlouisfed.org/graph/fredgraph.png?g=qUv
Qui abbiamo importanti modifiche di effetto per genere-i giovani hanno perso una percentuale enorme di posti di lavoro disponibili e non si erano ripresi completamente a partire dal 2014. Questo non è sorprendente, come la recessione è stata causata in gran parte dalla bolla immobiliare, e lavoratori edili sono per lo più giovani. Al contrario, le giovani donne hanno perso una piccola percentuale di posti di lavoro e si sono rapidamente riprese a livelli migliori rispetto alla pre-sessione.
Infine, esaminiamo i lavori per i giovani dai 25 ai 54 anni:
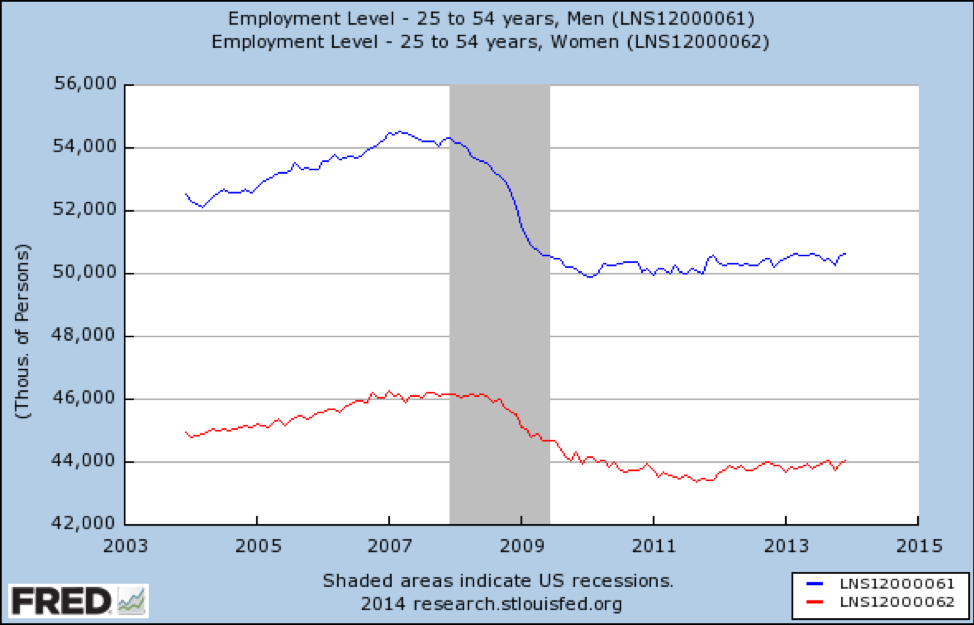
Fonte: https://fred.stlouisfed.org/graph/?id=LNS12000061
Qui vediamo un quadro molto desolante. In questa fascia di età, i posti di lavoro sono stati persi—più per gli uomini che per le donne—e a partire dal 2014 non si erano affatto ripresi.
Pertanto, esaminando la risposta del mercato del lavoro alla recessione del 2008, vediamo una sostanziale modifica degli effetti per età (il recupero dei posti di lavoro variava drasticamente per età) e, all’interno di alcune categorie di età, anche alcune prove di modifica degli effetti per sesso. Gli effetti della recessione sui posti di lavoro sono stati diversi per persone di età e generi diversi.
Questo è importante perché le implicazioni politiche sarebbero molto diverse. Immagina di lavorare come parte del governo federale e di cercare di progettare uno stimolo economico o un pacchetto di recupero. Se gli unici dati che avevi provenissero dal primo grafico, senza le disaggregazioni per età, le potenziali soluzioni politiche sarebbero molto diverse rispetto a se avessi anche accesso all’analisi stratificata per età.
Con confondendo, stai inizialmente ricevendo la risposta sbagliata perché il confonditore non è distribuito uniformemente tra i tuoi gruppi. Questo distorce la misura di associazione che calcoli (ricorda: avere piedi più grandi è associato alla velocità di lettura solo a causa della confusione per livello di grado). Quindi, invece, è necessario ricalcolare la misura dell’associazione, questa volta regolando per il confonditore.
Con la modifica degli effetti, inizialmente si ottiene anche la risposta sbagliata, ma questa volta è perché il campione contiene almeno 2 sottogruppi in cui l’associazione esposizione/malattia è diversa. In questo caso, è necessario separare permanentemente questi sottogruppi e riportare i risultati (che possono o non possono essere confusi da altre covariabili) separatamente per ogni strato: in questo caso, gli uomini che dormono meno hanno GPA più alti rispetto agli uomini che dormono di più, ma allo stesso tempo, le donne che dormono di più hanno GPA più alti rispetto alle donne che dormono meno.
Ecco una tabella riassuntiva che indica il processo per gestire potenziali confonditori e modificatori di effetti. Gran parte del processo è lo stesso indipendentemente dal tipo di covariabile che hai (in tutti i casi, devi misurare il covariabile durante il tuo studio e misurarlo bene!). Le aree di differenza sono mostrate in rosso.
| Confondendo | Modifica dell’effetto | |
| Prima di pianificare uno studio | Pensa a quali variabili potrebbero agire come confondenti in base a ciò che sai sull’esposizione/processo patologico in studio. | Pensa a quali variabili potrebbero fungere da modificatori di effetti in base a ciò che sai sul processo di esposizione/malattia in studio. |
| Durante uno studio | Raccogliere dati su eventuali potenziali covariabili-analisi stratificate / aggiustate non possono essere condotte senza dati sul covariabile! | Raccogliere dati su eventuali potenziali covariabili-analisi stratificate / aggiustate non possono essere condotte senza dati sul covariabile! |
| Analisi: Passo 1 | Calcola la misura grezza dell’associazione (ignorando la covariabile). | Calcola la misura grezza dell’associazione (ignorando la covariabile). |
| Analisi: Passo 2 | Calcola le misure di associazione specifiche dello strato, in modo tale che ogni livello della covariabile abbia una propria tabella 2 x 2. | Calcola le misure di associazione specifiche dello strato, in modo tale che ogni livello del covariabile abbia una propria tabella 2 x 2. |
| Analisi: Passo 3 | Se le misure specifiche dello strato sono simili tra loro e almeno il 10% diverse dal grezzo (che non rientra tra loro), allora il covariabile è un confondente. | Se le misure specifiche dello strato sono diverse l’una dall’altra e il grezzo si trova tra di esse, allora la covariabile è un modificatore di effetto. |
| I risultati di scrittura | Riportano una misura di associazione corretta che controlla il confonditore. | Segnalare le misure di associazione specifiche dello strato. |
Immaginate di fare uno studio trasversale di attività fisica e demenza nelle persone anziane, e si calcola un odds ratio non aggiustato (OR) di 2.0. Pensi che lo stato civile potrebbe essere un importante covariabile, quindi ti stratifichi per “attualmente sposato” contro “non attualmente sposato” (che include mai sposato, divorziato e vedovo). La OR tra le persone attualmente sposate è 3.1, e tra le persone non attualmente sposate la OR è 3.24. In questo caso, lo stato civile agisce da confondente e segnaliamo l’OR corretto (che sarebbe 3.18 o giù di lì).
Immagina di fare uno studio randomizzato di una dieta mediterranea per prevenire il parto pretermine nelle donne in gravidanza. Fai il processo e calcola un RR di 0,90. Pensi che forse la parità potrebbe essere un importante covariabile, quindi conduci un’analisi stratificata. Tra i nullipare, l’RR è 0,60 e tra i multipara, l’RR è 1,15. Questi sono diversi l’uno dall’altro, e il grezzo si trova tra di loro. In questo caso, parity agisce come un modificatore di effetti e quindi si segnalano separatamente i 2 RRS specifici dello strato.
Immaginate che si sta facendo uno studio caso-controllo del melanoma e l’uso prima lettino abbronzante. Il greggio OR è 3.5, ma forse il genere è un importante covariabile. L’analisi stratificata produce un OR di 3,45 tra gli uomini e 3,56 tra le donne. In questo caso, il covariabile (genere) non è né un confondente né un modificatore di effetto. Diciamo che non è un confondente perché (1) il greggio si trova tra le stime specifiche dello strato 2, ma anche (2) le stime specifiche dello strato non sono più del 10% diverse dal greggio. Diciamo che non è un modificatore di effetti perché, 3.45 e 3.56 non sono così diversi—in entrambi i casi, c’è un effetto sostanziale (circa 3.5 volte più alto). Riportiamo la stima approssimativa dell’associazione, in quanto non richiede né aggiustamenti né stratificazioni per tenere conto degli effetti del genere.
Sì! Di solito lo vediamo quando la covariabile in questione è una variabile continua, dicotomizzata ai fini del controllo della modifica dell’effetto. Ad esempio, se pensiamo che l’età potrebbe essere un modificatore di effetti, potremmo dividere il nostro campione in “vecchio” e “giovane” per l’analisi stratificata—diciamo, più vecchio di 50 contro 50 o più giovane. Nella misura in cui 51-year-olds non sono come 70-year-olds, potremmo perdere alcune importanti sfumature nei risultati, forse perché esiste nei dati un’ulteriore modifica dell’effetto con più categorie (che lascerebbero il potere a quasi nulla, se dovessimo riferire separatamente su strati aggiuntivi) o confusione” residua ” come discusso nel capitolo precedente. Ulteriori dettagli sono oltre lo scopo di questo libro, ma sappi che lo stesso covariabile può teoricamente agire sia come confondente che come modificatore di effetti, ma che raramente si vede questo nella pratica.
Conclusione
A differenza di confounding, di cui vogliamo eliminare gli effetti nella nostra analisi, la modifica degli effetti è una scoperta interessante in sé e per sé, e la segnaliamo. Per verificare la modifica dell’effetto, eseguire un’analisi stratificata. Se le misure di associazione specifiche dello strato sono diverse l’una dall’altra e il grezzo si trova tra di loro, allora è probabile che la variabile in questione agisca come modificatore di effetti. Riportare i risultati separatamente per ogni strato del covariabile.
Un ultimo, put-it-all-together tavolo:
| Se questi sono i tuoi ORs/RRs: | ||||
| Greggio/non corretto | Strato | Strato | Quindi il covariable è… | E si sarebbe report… |
| 2.0 | 1.0 | 3.2 | un effetto modificatore | il 2 strato-specifiche misure di associazione |
| 2.0 | 3.5 | 3.6 | un confounder | una regolata misura |
| 2.0 | 1.9 | 2.0 | niente di interessante | la misura grezzo |
Un errore sistematico in uno studio (alcune persone lo chiamano un pregiudizio, preferisco non farlo) causato da una terza variabile che interferisce nella relazione esposizione-malattia.
Si riferisce allo scenario in cui la relazione tra un’esposizione e un risultato varia sulla base di una terza variabile. Per esempio, forse yoga impedisce lesioni ACL nelle femmine, ma non maschi. Il sesso in questo scenario è il modificatore dell’effetto. La modifica dell’effetto non è la stessa di confondere.
La probabilità che il vostro studio troverà qualcosa che è lì. Potenza = 1-β; beta è il tasso di errore di tipo II. Piccoli studi, o studi di eventi rari, sono in genere sotto-alimentati.
Quanti figli ha avuto una donna. Le donne nullipare (aka nullipare) non hanno ancora avuto il loro primo figlio (possono essere incinte, ma non hanno ancora avuto il bambino), e le donne parose hanno avuto almeno un figlio precedente. Multiparas hanno avuto almeno due figli precedenti; primiparas hanno avuto un figlio precedente.
Questa è la prima gravidanza di una donna.
Questa donna ha avuto altri figli.