Il sistema solare: La Terra e la Luna

BY admin
|

I pianeti sono decine e centinaia di milioni di chilometri di distanza da noi. Per evitare l’uso di numeri così grandi, l’Unità astronomica (AU) viene adottata come unità di distanza, cioè la distanza media tra la Terra e il Sole, 149.600.000 km.La luce impiega 8 minuti e 19 secondi per coprire questa distanza.

La dimensione del Sistema Solare supera l’orbita di Plutone a 40 UA ed è definita come quella in cui la forza di attrazione del Sole è uguale alla forza di attrazione delle stelle più vicine a noi. Le dimensioni del sistema solare sarebbero quindi nell’ordine di 1,5 105 UA. Ovviamente, queste dimensioni sono molto piccole rispetto alle dimensioni della galassia o dell’Universo visibile. Le unità che vengono prese per misurare queste enormi distanze sono l’anno luce e il parsec che equivale a 206 265 UA o 3,26 anni luce.

I pianeti del Sistema Solare sono divisi in due gruppi: il gruppo terrestre formato da Mercurio, Venere, Terra e Marte e il gruppo dei pianeti giganti formato da Giove, Saturno, Urano e Nettuno.

Tutti i pianeti tranne Venere e Mercurio hanno satelliti, la maggior parte dei quali appartengono ai pianeti giganti. La Terra, Giove, Saturno e Nettuno hanno i satelliti più grandi: la Luna, i satelliti di Giove scoperti da Galileo (Io, Europa, Ganimede, Callisto), il satellite Titano di Saturno e Tritone di Nettuno.

Gli asteroidi occupano una vasta regione anulare tra le orbite di Marte e Giove, ad una distanza media di 2,75 UA dal Sole. L’asteroide più grande è Cerere che ha un diametro di 1000 km.

Le comete, che sono state catalogate circa 600, sono divise in due gruppi, breve periodo (meno di 20 anni) e lungo periodo (oltre 20 anni). Ci sono diverse ipotesi sull’origine delle comete, tra cui quella dell’astronomo olandese J. Oort.

Oltre ai corpi menzionati nello spazio interplanetario, c’è un gran numero di particelle di diverse dimensioni, prevalentemente quelle con una massa di millesimi o milionesimi di grammo, che sono chiamate polvere meteorica. La formazione di queste particelle è probabilmente dovuta alla collisione di corpi più grandi (asteroidi) e alla loro successiva frammentazione durante l’esistenza e l’evoluzione del Sistema Solare.

La polvere meteorica è responsabile del fenomeno della luce zodiacale, che si osserva dopo il tramonto o prima dell’alba, a causa della dispersione della luce da parte di queste particelle di polvere. La maggior parte delle particelle evapora entrando nell’atmosfera terrestre (ad altitudini comprese tra 80 e 120 km), solo una piccola percentuale raggiunge la superficie terrestre.

vediamo ora alcuni dati relativi ai pianeti del Sistema Solare

Prima del Sole

Corpo celeste Radio Massa
Sole 6.96·108 m 1.98·1030 kg

Quindi, al di fuori della Terra

Corpo celeste semi-asse maggiore Periodo Massa
Terra 149.6·109 m 1 anno=365.26 giorni 5.98·1024 kg

e il resto dei pianeti

Pianeta semi-asse maggiore (AU) Eccentricità Periodo (anni) Massa
Mercurio 0.387 0.206 0.24 0.06
Venere 0.723 0.007 0.62 0.82
Terra 1.000 0.017 1.00 1.00
Marte 1.524 0.093 1.88 0.11
Giove 5.203 0.048 11.86 318
Saturno 9.539 0.056 29.46 95.1
Urano 19.182 0.047 84.01 14.6
Nettuno 30.058 0.009 164.8 17.2

Nella seguente tabella vengono forniti dati supplementari:

  • L’inclinazione del piano dell’orbita del pianeta rispetto all’eclittica (piano dell’orbita della Terra)
  • Il periodo di rotazione attorno al suo asse. È stato molto difficile misurare questa grandezza per pianeti come Mercurio e Venere. I gusci gassosi di Giove, Saturno, Urano e Nettuno possiedono la proprietà della rotazione differenziale, cioè i loro periodi di rotazione variano in base alla latitudine.
  • L’inclinazione dell’asse di rotazione rispetto al piano dell’orbita. Nel caso di Venere è 177º che equivale a dire che l’inclinazione dell’asse è 3º ma la direzione di rotazione è inversa. Lo stesso argomento si applica a Urano, che indica che l’asse di rotazione di Urano è quasi nel piano della sua orbita.
Pianeta Inclinazione dell’orbita Periodo di rotazione Densità g/cm3 Radio equatore (km) Inclinazione dell’asse No. di satelliti
Mercurio 7°.0 58d.6 5.44 2 439 <30º 0
Venere 3°.4 243d 5.24 6 051 177 ° 0
Terra 0 23h.9 5.52 6 378 23.5 1
Marte 1 ° 8 24 ore.6 3.95 3 394 25º.2 2
Giove 1st.3 9 h.9 1.33 71 398 3°.1 16
Saturno 2°.5 10 h.2 0.69 60 000 26º.4 17
Urano 0º.8 10h.8 1.26 25 400 98º 5
Nettuno 1.8 15h.8 1.67 24 750 29º 2
Vedere i pianeti fino:

Satelliti

Infine, forniamo alcuni dati riguardanti i principali satelliti dei pianeti. Giove e Saturno hanno molti satelliti che sono molto più grandi di quelli di Marte, ma menzioniamo solo quelli che sono di dimensioni simili o più grandi della nostra Luna.

Pianeta Satelliti Densità g/cm3 medio Raggio (km) Radio orbita (103 km) Periodo (giorni)
Terra Luna 3.33 1 738 384.4 27.32
Marte Phobos 2.1 13.5 9.38 0.319
Deimos 2.1 7.5 23.46 1.262
Giove Io 3.53 1 820 421.6 1.769
Europa 3.03 1 565 670.9 3.551
Ganimede 1.93 2 638 1 070 7.155
Calisto 1.83 2 410 1 880 16.689
Saturno Titan 1.9 2 575 1 221.9 15.95
Nettuno Tritone 2 200 394.7 5.84

Attività

  1. Determinare la massa del pianeta Giove dai dati radio e il periodo di rivoluzione di uno dei suoi satelliti.

    2. Esempio: determinare la massa del pianeta Giove sapendo che il raggio dell’orbita di Io è di 421.600 km e che il suo periodo di rivoluzione è di 1.769 giorni. Fatto: la costante G è 6,67 * 10-11 Nm2 / kg2

  2. Determina il raggio dell’orbita di un satellite del pianeta Giove dalla massa di quel pianeta e il periodo di rivoluzione del satellite.

    3. Esempio: Calcola il raggio dell’orbita del satellite Callisto sapendo che il suo periodo di rivoluzione è di 16.689 giorni e la massa del pianeta Giove è di 1.901·1027 kg. Dati: la costante G è 6,67 * 10-11 Nm2/kg2

  3. Determina l’intensità del campo gravitazionale g sulla superficie dei pianeti e di alcuni satelliti, dai dati della loro massa M e del loro raggio R o della loro densità ρ e del loro raggio.

    4. g=G M R 2 = 4π 3 GpR

    Dati: la costante G è 6.67 * 10-11 Nm2 / kg2

La Luna

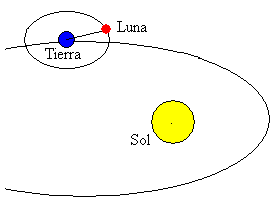
La Luna è uno dei corpi più grandi del sistema solare. La sua orbita è quasi circolare (eccentricità ε = 0,05)e il piano della sua orbita è inclinato di 5º rispetto al piano dell’orbita terrestre.

La distanza media tra il centro della Terra e la Luna è di 384.400 km.Il suo periodo di rotazione intorno alla Terra è di 27.322 giorni. Il cambiamento della posizione della Luna rispetto al Sole dà origine alle fasi della Luna.

La Luna presenta sempre la stessa faccia all’osservatore terrestre, a causa dell’effetto delle forze di marea che la Terra esercita sulla Luna. Il che significa che il periodo di rotazione della Luna attorno al suo asse coincide con il tempo necessario per completare un’orbita attorno alla Terra.

La Luna è l’oggetto celeste che più ha affascinato la specie umana. L’ex Unione Sovietica inviò per la prima volta una nave automatica che atterrò sulla superficie della Luna nel 1959. Il 20 luglio 1969 Neil Armstrong accompagnato da Edwin Aldrin furono i primi uomini a camminare sulla superficie della Luna come parte della missione Apollo 11. L’ultima visita degli astronauti americani sulla Luna ebbe luogo nel 1972.

L’origine della Luna sembra incerta, ci sono diverse teorie:

  • si è formata al tempo stesso la Terra con il materiale da una nebulosa

  • un corpo celeste è diviso in due parti, dando vita per la Terra e la Luna

  • Che la Luna formata altrove, e ‘ stata catturata dalla Terra

  • Che la Terra si è scontrato con un oggetto celeste di grandi dimensioni (circa le dimensioni di Marte o superiore), e che la Luna si è formata con il materiale espulso da questa collisione.

Quest’ultima teoria sembra, al momento, la più accettata dalla comunità scientifica.

Percorso della Luna

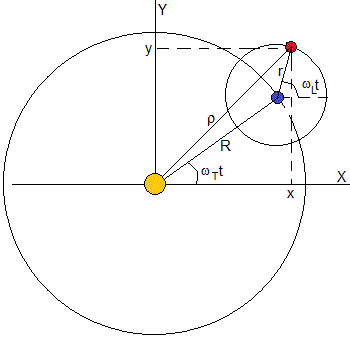
Considera un pianeta e il suo satellite. Il pianeta descrive un’orbita circolare di raggio R attorno alla sua stella con velocità angolare costante wT=2π / PT, con PT che è il periodo o il tempo che porta a una svolta completa. Il satellite descrive un’orbita circolare coplanaria di raggio r con velocità angolare costante wL=2π/PL, PL essere il periodo o il tempo necessario per fare una rivoluzione completa

la posizione del satellite rispetto ad un sistema di riferimento la cui origine è la stella, è

x=Rcos( ω T )+rcos( ω t ) y=Risiko( ω T )+risiko( ω t )

È α=wT/wL

{ x=Rcos( α ω t )+rcos( ω t ) y=Risiko( α ω t )+risiko( ω t ) { x=Rcos( α 2π P L t )+rcos( 2π-P-L-t ) y=Risiko( α 2π P L t )+risiko( 2π P L t )

chiameremo τ=t/PL

x R = cos( α * 2πτ) + r R cos( 2πτ) e R =sin( α·2πτ) + r r sin( 2πτ)

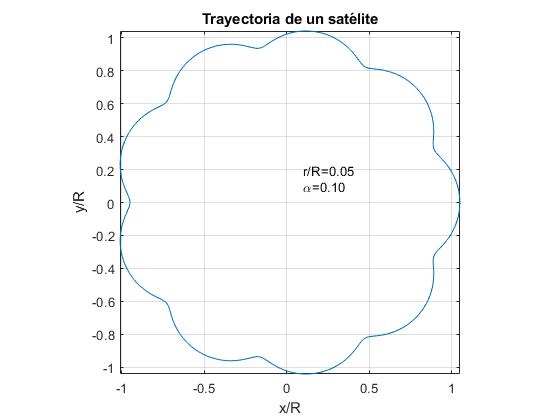
rappresentiamo la traiettoria di un satellite per α=0.1 e per tre valori del rapporto r/R.

  • r/R<α. Esempio, r / R=0.05
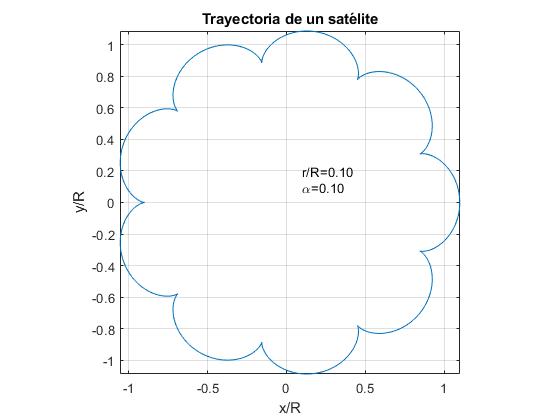
  • r/R=α. Esempio, r / R=0.1
  • r/R >α. Esempio, r / R=0.15
alfa=0.1;r=0.15;fplot(@(t) r*cos(2*pi*t)+cos(2*pi*alfa*t), @(t) r*sin(2*pi*t)+sin(2*pi*alfa*t),)text(0.1,0.1,sprintf('\alpha=%1.2f',alfa))text(0.1,0.2,sprintf('r/R=%1.2f',r))axis equalgrid onxlabel('x/R')ylabel('y/R')title('Trayectoria de un satélite')

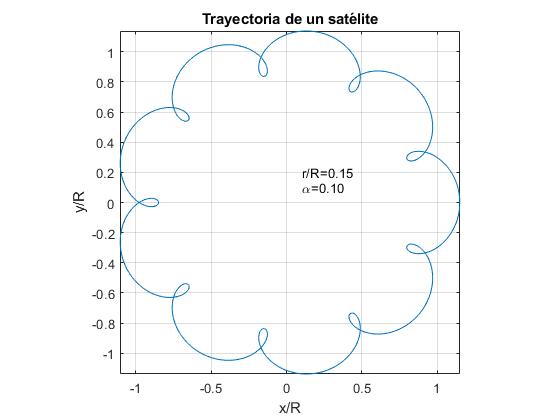
Per il caso di la Terra e la Luna, i dati sono:

  • raggio di Luna orbita: r=384.4·106 m, periodo PL = 27.32 d
  • raggio dell’orbita terrestre: R = 149,6·109 m, periodo PT = 365,26 d

α = peso/peso = PL / PT = 0,0748. r / R=0.0026

L’orbita della Luna assomiglierà alla prima figura. Nella rappresentazione grafica della traiettoria della Luna per questi valori di α e r/R non apprezza le oscillazioni della distanza radiale tra il Sole e la Luna

Accelerazione della Luna

La distanza r tra il Sole e la Luna, è

ρ 2 = x 2 + y 2 = R 2 + r 2 +2rRcos( ( ω L − ω T )t )

calcoliamo rettangolare componenti di accelerazione

{ dx dt =− ω T Risiko( ω T )− ω L risiko( ω t ) dy dt = ω T Rcos( ω T )+ ω L rcos( ω t ) { x = d 2 x d t 2 =− ω T 2 Rcos( ω T )− ω L 2 rcos( ω t ) y = d 2 y d t 2 =− ω T 2 Risiko( ω T )− ω L 2 risiko( ω t )

la componente radiale dell’accelerazione

per ρ = a → · ρ → r = a x x+ y x 2 + y 2 =− ω T 2 R 2 + ω L 2 r 2 +( ω T 2 + ω L 2 )Rrcos( ( ω L − ω T )t ) R 2 + r 2 +2 rr cos( ( ω L − ω T )t )

I valori minimo e massimo sono ottenuti quando cos((wL-wT)t)=±1

max =− ω T 2 R 2 + ω L 2 r 2 +( ω T 2 + ω L 2 )Rr R 2 + r 2 +2 rr =−( ω T 2 R+ ω L 2 r ) min =− ω T 2 R 2 + ω L 2 r 2 −( ω T 2 + ω L 2 )Rr R 2 + r 2 -2 rr =−( ω T 2 R− ω L 2 r ) 

>> R=149.6e9; %Tierra>> r=384.4e3; %Luna>> wT=2*pi/(365*24*60*60) %velocidad angular TierrawT = 1.9924e-07>> wL=2*pi/(27.32*24*60*60) %velocidad angular TierrawL = 2.6619e-06>> aM=-(wT^2*R+wL^2*r)aM = -0.0059>> am=-(wT^2*R-wL^2*r)am = -0.0059

La Luna è l’unico satellite del Sistema Solare, di cui la componente radiale dell’accelerazione è negativa, si dice che ‘la Luna cade verso il Sole,’

fasi della Luna

La figura mostra la Luna in posizioni diverse nella sua orbita intorno alla Terra. Il Sole è lontano illuminando entrambi i corpi celesti (nella parte superiore della figura)

Metà della Luna è illuminata dal Sole (in colore bianco) e metà della Luna più vicina alla Terra è visibile dall’osservatore terrestre. Mentre la Luna si muove intorno alla Terra vediamo diverse frazioni della parte illuminata dal Sole (le aree gialle).

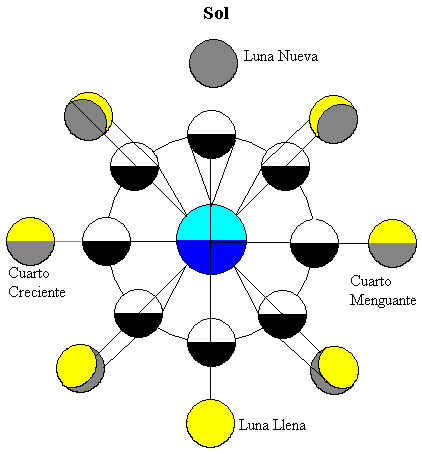
  • Quando la Luna è tra la Terra e il Sole, la parte della Luna più vicina alla Terra è scura, quindi non possiamo vedere la Luna, questa fase è chiamata Luna Nuova.

  • Quando la Terra è tra il Sole e la Luna, la parte della Luna più vicina alla Terra è la metà illuminata, questa fase è chiamata Luna piena.

  • Quando la Luna è in posizioni intermedie, solo la metà della parte più vicina della Terra è illuminata. Pertanto, vediamo solo un quarto della Luna, queste due fasi sono chiamate Quarti, Aumentando o diminuendo a seconda che la parte illuminata visibile dalla Terra tenda a crescere o diminuire.

Nota: Questo programma interattivo cerca di spiegare le fasi della Luna, ma si tratta di una fedele rappresentazione dell’orbita della Luna, che forma un angolo di circa 5 ° rispetto al piano dell’eclittica (l’orbita della Terra intorno al Sole), o l’orientamento dell’asse della Terra, che è di circa 23º con la normale al piano dell’eclittica.

Una linea rossa è stata tracciata attraverso la Luna in modo che il lettore possa apprezzare la coincidenza del periodo di rotazione della Luna attorno al suo asse e il tempo necessario per completare un’orbita attorno alla Terra e quindi la Luna ha sempre la stessa faccia alla Terra.

Eclissi di Luna

Eclissi di Luna si verificano ogni volta che la Luna è in piena fase e ogni volta che il Sole, la Terra e la Luna sono in linea retta. Quindi la Luna è nell’ombra prodotta dalla Terra come mostrato nella figura.

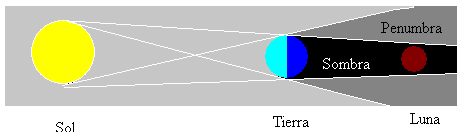
Esistono altri tipi di eclissi lunare, che dipendono dall’allineamento dei tre corpi celesti. La Luna può essere in un’area non illuminata (ombra) o parzialmente illuminata (penombra).

L’eclissi solare si verifica quando la Luna si trova tra il Sole e la Terra, la Luna è in una nuova fase. La Luna è 400 volte più piccola del Sole, ma la Luna è 400 volte più vicina alla Terra, quindi la dimensione apparente di entrambi i corpi visti dalla Terra è quasi la stessa. La Luna può quindi produrre un’eclissi totale del Sole, se osservata nella zona d’ombra proiettata dalla Luna sulla Terra.

Dati luna

Massa (kg) 7.349·1022
Raggio (km) 1737. 4
Densità media (g/cm3) 3.34
Distanza media della Terra (km) 384 000
Periodo di orbita (giorni) 27.32166
l’Accelerazione di gravità all’equatore (m/s2) 1.62
Eccentricità dell’orbita 0.0549
Inclinazione dell’orbita (gradi) 5.1454

  1. Calcolare il raggio dell’orbita circolare della Luna intorno alla Terra, sapendo che il periodo è 27.32 giorni. Calcola anche la velocità della Luna. Dati: G = 6,67 * 10-11 Nm2 / kg2, la massa della Terra è M = 5,98 * 1024 kg.

  2. Calcola l’accelerazione di gravità g sulla superficie della Luna.

  3. Calcola il quoziente tra il diametro del Sole e il diametro della Luna. Calcola il rapporto tra la distanza media tra il Sole e la Terra e la Luna e la Terra. Dati: raggio di sole 6.96 * 108 m, Terra di Mezzo-Sole distanza 1.49 * 1011 m

  4. Calcola la posizione del centro di massa del sistema Terra-Luna, misurata dal centro della Terra.

  5. Calcola la forza di attrazione della Terra sulla Luna, confrontala con la forza di attrazione del Sole sulla Luna. Dato: Massa del sole, 1.98 * 1030 kg

Riferimenti

M. Marov. Pianeti del Sistema Solare. Casa Editrice Mir.

Scopri di più sui pianeti in Quanti pianeti ci sono nel nostro Sistema solare?. ComofuncionaQue.com

Per la sezione ‘Traiettoria della Luna’

David C. Johnston. Percorsi cicloidali in fisica come sovrapposizioni di moti traslazionali e rotazionali. Essere. J. Phys.87 (10), ottobre 2019, pp. 808-810

La Luna vira sempre verso il Sole. Pagine di matematica.